wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 14 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Ci sono 7 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 126 031 volte
Un trinomio è un'espressione algebrica costituita da tre termini. Molto probabilmente, inizierai a imparare a scomporre i trinomi quadratici, cioè scritti nella forma ax2 + bx + c. Esistono diversi trucchi da imparare che si applicano ai differenti tipi di trinomio quadratico, ma diventerai più bravo e più veloce solo con la pratica. I polinomi di grado superiore, con termini come x3 o x4, non sono sempre risolvibili con gli stessi metodi, ma spesso è possibile utilizzare semplici scomposizioni o sostituzioni per trasformarli in problemi che possono essere risolti come qualsiasi formula quadratica.
Passaggi
Scomporre x2 + bx + c
-
1Impara la tecnica FOIL. Potresti avere già imparato il metodo FOIL, cioè "First, Outside, Inside, Last" ovvero "Primo, fuori, dentro, ultimo", per moltiplicare delle espressioni come (x + 2)(x + 4). È utile sapere come funziona prima di arrivare alla scomposizione:
- Moltiplica i termini First: (x+2)(x+4) = x2 + __
- Moltiplica i termini Outside: (x+2)(x+4) = x2+4x + __
- Moltiplica i termini Inside: (x+2)(x+4) = x2+4x+2x + __
- Moltiplica i termini Last: (x+2)(x+4) = x2+4x+2x+8
- Semplifica: x2+4x+2x+8 = x2+6x+8
-
2Cerca di capire la scomposizione in fattori. Quando si moltiplicano due binomi con il metodo FOIL, si arriva a un trinomio (un'espressione con tre termini) nella forma ax2 + bx + c, dove a, b e c sono numeri qualunque. Se parti da un'equazione in questa forma, puoi scomporla nei due binomi.
- Se l'equazione non è scritta in questo ordine, sposta i termini. Ad esempio, riscrivi 3x - 10 + x2 come x2 + 3x - 10.
- Siccome l'esponente più alto è 2 (x2), questo tipo di espressione è "quadratica".
-
3Scrivi uno spazio per la risposta in forma FOIL. Per ora, ti basta scrivere (__ __) ( __ __) nello spazio dove potrai scrivere la risposta. La completeremo dopo.
- Non scrivere ancora + o - tra i termini vuoti, dato che non sappiamo quali saranno.
-
4Compila i primi termini (First). Per gli esercizi semplici, dove il primo termine del tuo trinomio è solo x2, i termini in prima (First) posizione saranno sempre x e x. Questi sono i fattori del termine x2, visto che x per x = x2.
- Il nostro esempio x2 + 3 x - 10 inizia con x2, quindi possiamo scrivere:
- (x __)(x __)
- Faremo degli esercizi più complicati nella sezione successiva, tra cui i trinomi che iniziano con un termine come 6x2 o -x2. Per ora, segui il problema di esempio.
-
5Utilizza la scomposizione per indovinare gli ultimi (Last) termini. Se torna indietro e rileggi il passaggio del metodo FOIL, vedrai che moltiplicando tra loro gli ultimi termini (Last) avrai il termine finale del polinomio (quello senza x). Così, per fare la scomposizione, abbiamo bisogno di trovare due numeri che, moltiplicati, diano l'ultimo termine.
- Nel nostro esempio, x2 + 3 x - 10, l'ultimo termine è -10.
- Quali sono i divisori di -10? Quali due numeri moltiplicati insieme danno -10?
- Ci sono alcune possibilità: -1 per 10, -10 per 1, -2 per 5 o -5 per 2. Scriviti queste coppie da qualche parte per ricordarle.
- Non cambiare ancora la nostra risposta. Al momento, siamo a questo punto: (x __)(x __).
-
6Prova quali possibilità vanno bene con la moltiplicazione esterna e interna (Outside e Inside) dei termini. Abbiamo ristretto gli ultimi termini (Last) a qualche possibilità. Vai per tentativi per provare ogni possibilità, moltiplicando i termini esterni e interni (Outside e Inside) e confrontando il risultato con il nostro trinomio. Ad esempio:
- Il nostro problema originale ha un termine in "x" che è 3x, che è quello che vogliamo trovare con questa prova.
- Prova con -1 e 10: (x - 1)(x + 10). Esterno + interno = Outside + Inside = 10x - x = 9x. Non vanno bene.
- Prova con 1 e -10: (x + 1)(x - 10). -10x + x = -9x. Non è vero. Infatti, una volta provato con -1 e 10, sai che 1 e -10 daranno proprio la risposta contraria alla precedente: -9x anziché 9x.
- Prova con -2 e 5: (x - 2)(x + 5). 5x - 2x = 3x. Questo corrisponde al polinomio originale, quindi questa è la risposta corretta: (x - 2)(x + 5).
- Nei casi semplici come questo, quando non esiste un numero davanti alla x, puoi utilizzare una scorciatoia: basta sommare insieme i due fattori e mettere dopo una "x" (-2 + 5 → 3x). Questo non funziona con i problemi più complicati, però, quindi è bene ricordare la "via lunga" sopra descritta.
Pubblicità
Scomporre Trinomi più Complessi
-
1Utilizza la scomposizione semplice per facilitare i problemi più complicati. Supponiamo di voler semplificare 3x2 + 9x - 30. Cerca un divisore comune a ciascuno dei tre termini (il massimo comun divisore, MCD).[1] In questo caso, è 3:
- 3x2 = (3)(x2)
- 9x = (3)(3x)
- -30 = (3)(-10)
- Pertanto, 3x2 + 9 x - 30 = (3) (x2 + 3 x -10). Possiamo scomporre di nuovo il trinomio utilizzando la procedura riportata nella sezione precedente. La nostra risposta finale sarà (3)(x - 2)(x + 5).
-
2Cerca delle scomposizioni più complicate. A volte, potrebbe trattarsi di variabili o potrebbe essere necessario scomporre un paio di volte per trovare la più semplice espressione possibile. Ecco alcuni esempi:
- 2x2y + 14xy + 24y = (2y)(x2 + 7x + 12)
- x4 + 11x3 - 26x2 = (x2)(x2 + 11x - 26)
- -x2 + 6x - 9 = (-1)(x2 - 6x + 9)
- Non dimenticare di scomporre ulteriormente, utilizzando la procedura nel metodo 1. Controlla il risultato e trova esercizi simili agli esempi presenti nella parte inferiore di questa pagina.
-
3Risolvi i problemi con un numero davanti alla x2. Alcuni trinomi non possono essere semplificati fino a ottenere dei fattori. Impara a risolvere dei problemi come 3x2 + 10x + 8, poi esercitati da solo con i problemi di esempio nella parte inferiore della pagina:
- Imposta così la soluzione: (__ __)(__ __)
- I nostri primi termini (First) avranno ognuno una x e si moltiplicheranno insieme per dare 3x2. C'è una sola opzione possibile qui: (3x __)(x __).
- Elenca i divisori di 8. Le possibili scelte sono 8 x 1 o 2 x 4.
- Provali utilizzando i termini esterno e interno (Outside e Inside). Nota che l'ordine dei fattori è importante, poiché il termine esterno viene moltiplicato per 3x invece che per x. Prova tutte le combinazioni possibili finché non ottieni un esterno + interno (Outside + Inside) che danno 10x (dal problema originale):
- (3x+1)(x+8) → 24x+x = 25x no
- (3x+8)(x+1) → 3x+8x = 11x no
- (3x+2)(x+4) → 12x+2x=14x no
- (3x+4)(x+2) → 6x+4x=10x sì È la scomposizione corretta.
-
4Utilizza la sostituzione per i trinomi di grado più elevato. Il libro di matematica potrebbe prenderti di sorpresa con un polinomio di esponente alto, come x4, anche dopo aver semplificato il problema. Prova a sostituire una nuova variabile in modo da ritrovarti con un esercizio che sai risolvere. Ad esempio:
- x5+13x3+36x
- =(x)(x4+13x2+36)
- Usiamo una nuova variabile. Supponiamo che y = x2 e sostituiamo:
- (x)(y2+13y+36)
- =(x)(y+9)(y+4). Ora torniamo alla variabile iniziale.
- =(x)(x2+9)(x2+4)
- =(x)(x±3)(x±2)
Pubblicità
Scomposizione di Casi Speciali
-
1Verifica con i numeri primi. Controlla se la costante nel primo o terzo termine del trinomio è un numero primo. Un numero primo è divisibile unicamente solo per se stesso e 1, quindi esiste solo un paio di possibili fattori.
- Per esempio, nel trinomio x2 + 6x + 5, 5 è un numero primo, per cui il binomio deve essere nella forma (__ 5)(__ 1) .
- Nel problema 3x2 + 10x + 8, 3 è un numero primo, così il binomio deve essere nella forma (3x __) ( x __).
- Per il problema 3x2 + 4x + 1, 3 e 1 sono numeri primi, quindi l'unica soluzione possibile è (3x + 1)(x + 1). (Dovresti ancora moltiplicare per controllare il lavoro svolto, poiché alcune espressioni non possono proprio essere fattorizzate – per esempio, 3x2 + 100x + 1 non è scomponibile in fattori.)
-
2Controlla per vedere se il trinomio è un quadrato perfetto. Un trinomio quadrato perfetto può essere scomposto in due binomi identici e il fattore solitamente è scritto (x + 1)2 invece che (x+1)(x+1). Ecco alcuni quadrati che si presentano spesso nei problemi:
- x2+2x+1=(x+1)2 e x2-2x+1=(x-1)2
- x2+4x+4=(x+2)2 e x2-4x+4=(x-2)2
- x2+6x+9=(x+3)2 e x2-6x+9=(x-3)2
- Un trinomio quadrato perfetto nella forma ax2 + bx + c ha sempre i termini a e c che sono quadrati perfetti positivi (ad esempio 1, 4, 9, 16 o 25) e un termine b (positivo o negativo) che equivale a 2(√a * √c).[2]
-
3Verifica se non esiste alcuna soluzione. Non tutti i trinomi possono essere presi in considerazione. Se sei bloccato su un trinomio (ax2 + bx + c), utilizza la formula quadratica per trovare la risposta. Se le uniche risposte sono la radice quadrata di un numero negativo, non esiste nessuna soluzione reale, quindi non ci sono dei fattori.
- Per i trinomi non-quadratici, utilizza il criterio di Eisenstein, descritto nella sezione Consigli.
Pubblicità
Problemi d’Esempio con Risposte
-
Trova delle risposte ai problemi ingannevoli sulle scomposizioni. Li abbiamo già semplificati in problemi più facili, quindi cerca di risolverli utilizzando i passaggi visti nel metodo 1, poi controlla qui il risultato:
- (2y)(x2 + 7x + 12) = (x+3)(x+4)
- (x2)(x2 + 11x - 26) = (x+13)(x-2)
- (-1)(x2 - 6x + 9) = (x-3)(x-3) = (x-3)2
-
Prova con problemi di scomposizione più difficili. Questi problemi hanno un fattore comune in ogni termine che deve essere prima raccolto. Evidenziare lo spazio dopo i segni di uguale per vedere la risposta in modo da poter controllare il lavoro:
- 3 x 3 + 3 x 2 -6 x = (3x)(x+2)(x-1) ← evidenzia lo spazio per vedere la risposta
- -5x3y2+30x2y2-25y2x = (-5xy^2)(x-5)(x-1)
-
Esercitati con problemi difficili. Questi problemi non possono essere scomposti in equazioni più facili, quindi è necessario elaborare una risposta sotto forma di ( x + _)(_x + __) per tentativi ed errori:
- 2x2+3x-5 = (2x+5)(x-1) ← evidenzia per vedere la risposta
- 9 x 2 + 6 x + 1 = (3x+1)(3x+1)=(3x+1)2 (Suggerimento: potrebbe essere necessario provare più di una coppia di fattori per 9 x.)
Consigli
- Se non riesci a capire come scomporre un trinomio quadratico (ax2 + bx + c), puoi sempre utilizzare la formula quadratica per trovare la x.
- Nonostante non sia obbligatorio, puoi utilizzare i criteri di Eisenstein per determinare rapidamente se un polinomio è irriducibile e non può essere scomposto. Questi criteri funzionano per qualsiasi polinomio, ma vanno particolarmente bene per i trinomi. Se c'è un numero primo p che è un fattore degli ultimi due termini e soddisfa le seguenti condizioni, allora il polinomio è irriducibile:
- Il termine costante (per un trinomio nella forma ax2 + bx + c, questo è il c) è un multiplo di p, ma non di p2.
- Il termine iniziale (che qui è a) non è un multiplo di p.
- Per esempio, permette di determinare rapidamente che 14x^9 + 45x^4 + 51 è irriducibile, poiché 45 e 51, ma non 14, sono divisibili per il numero primo 3 e 51 non è divisibile per 9.
Avvertenze
- Sebbene sia vero per i quadratici, i trinomi scomponibili non sono necessariamente il prodotto di due binomi. Un esempio opposto è x^4 + 105x + 46 = (x^2 + 5x + 2)(x^2 - 5x + 23).
Riferimenti
- ↑ http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut28_facttri.htm
- ↑ http://www.themathpage.com/alg/perfect-square-trinomial.htm
- http://www.wtamu.edu/academic/anns/mps/math/mathlab/int_algebra/int_alg_tut28_facttri.htm
- http://www.themathpage.com/alg/factoring-trinomials.htm
- http://www.themathpage.com/alg/perfect-square-trinomial.htm
- http://www.algebrahelp.com/lessons/factoring/trinomial/
- http://en.wikipedia.org/wiki/Polynomial
Informazioni su questo wikiHow
Per scomporre un trinomio, assicurati di conoscere il metodo di moltiplicazione FOIL (First, Outside, Inside, Last, vale a dire, Primo, fuori, dentro, ultimo) e come scomporre. Scrivi uno spazio per la risposta in formato FOIL e compila i primi termini (First). Quindi, utilizza la scomposizione per indovinare gli ultimi termini (Last). Per fare la scomposizione, trova due numeri che moltiplicati diano l’ultimo termine (Last). Ripeti il passaggio finché non riduci a poche possibilità gli ultimi termini (Last). Dopodiché, controlla quali possibilità vanno bene con la moltiplicazione esterna e interna dei termini (Outside e Inside). Trovati i termini che corrispondono al polinomio originale, avrai ottenuto la risposta corretta. Continua a leggere l’articolo se vuoi imparare come scomporre i trinomi quando le variabili hanno un coefficiente!
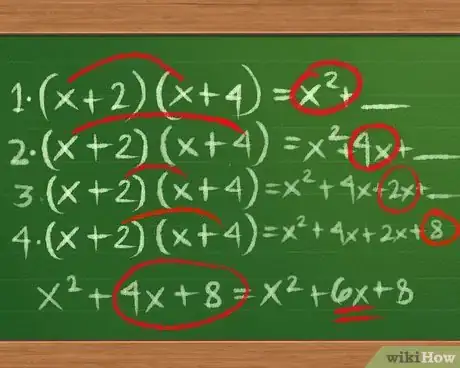
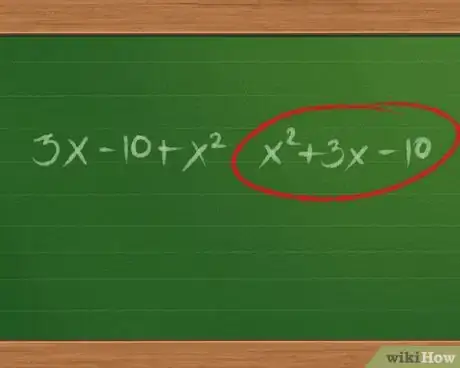

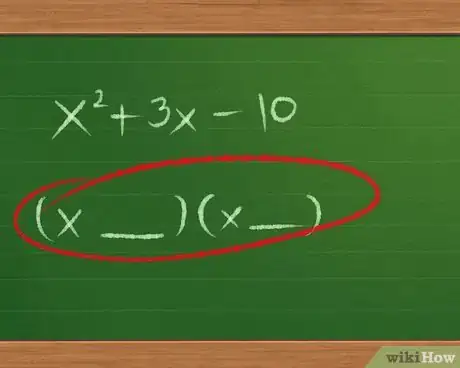
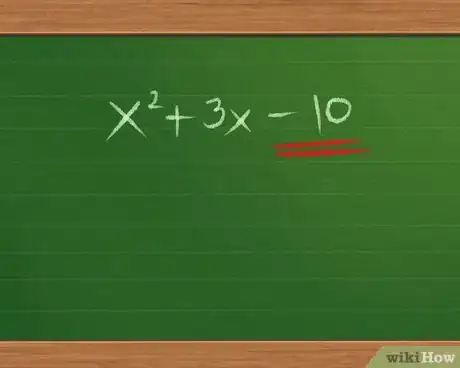
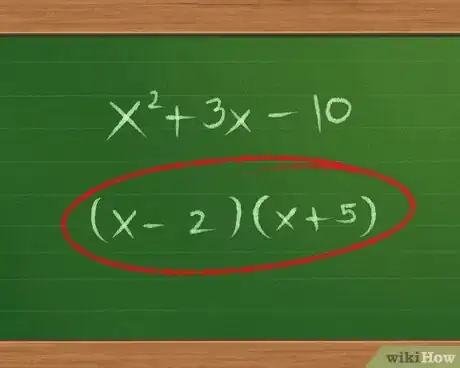


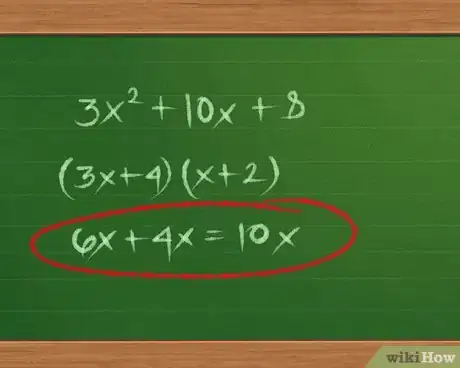

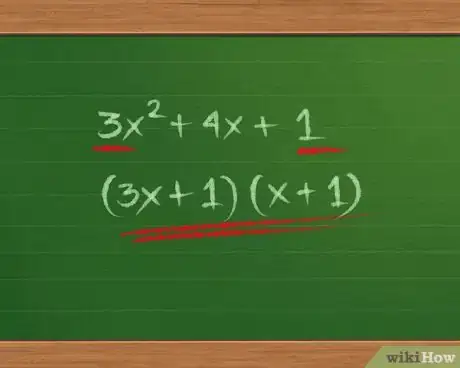
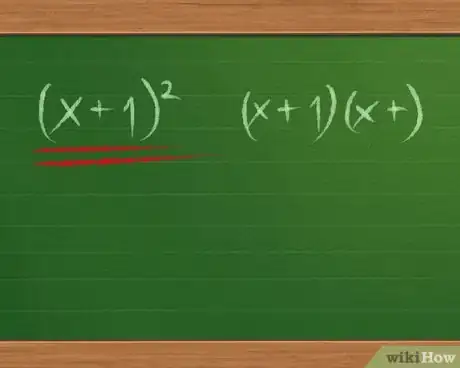
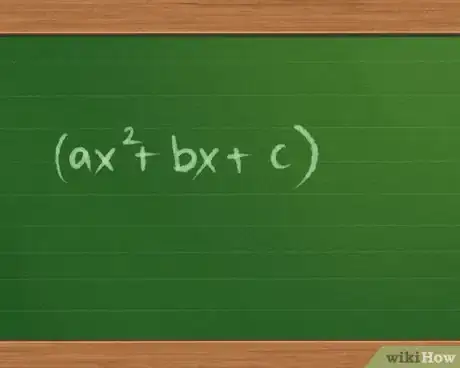
-Step-31-Version-2.webp)




-to-Grams-(g)-Step-12-Version-4.webp)







-Step-31-Version-2.webp)