Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 24 882 volte
Un vettore è la rappresentazione grafica di una forza fisica. Potrebbe indicare un movimento, per esempio un aereo che viaggia in direzione nordest alla velocità di 640 km/h; potrebbe anche identificare una forza, come una palla che rotola giù da un tavolo e cade in direzione diagonale a causa della gravità e della sua velocità iniziale di rotolamento. Spesso si rivela utile scomporre il vettore nelle sue componenti e calcolare queste ultime; in altri termini, significa individuare quanta forza (o velocità o qualsiasi altra grandezza vettoriale rappresentata) viene applicata lungo la direzione orizzontale e quanta lungo la direzione verticale. Puoi procedere con un metodo grafico grazie alla geometria elementare; per ottenere calcoli più precisi occorre utilizzare la trigonometria.
Passaggi
Per Via Grafica
-
1Scegli la scala opportuna. Per rappresentare graficamente un vettore e le sue componenti devi decidere la scala; questa deve essere abbastanza grande da permetterti di lavorare in maniera agile e precisa, ma sufficientemente piccola affinché il vettore possa essere disegnato.[1]
- Per esempio, supponi di dover lavorare con un vettore che rappresenta la velocità di un corpo che viaggia a 320 km/h in direzione nordest. Se stai usando la carta millimetrata standard con 5 quadretti ogni mezzo centimetro, puoi decidere che ciascuno di essi corrisponda a 4 km/h, il che significa che ogni centimetro equivale a 40 km/h.
- Non è necessario disegnare un sistema di assi cartesiani, perché la posizione del vettore rispetto all'origine è irrilevante. Il tuo problema è misurare il vettore di per sé e non trovare la sua posizione in un sistema di riferimento bidimensionale o tridimensionale; stai usando la carta millimetrata come utile strumento di misurazione, la posizione non importa.
-
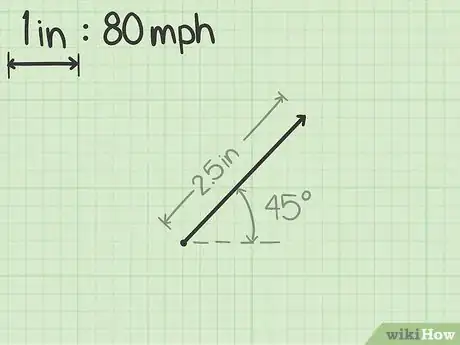
2Disegna il vettore rispettando la scala. È fondamentale che questo passaggio avvenga con la maggiore precisione possibile; devi indicare correttamente sia la direzione sia la lunghezza del vettore.[2]
- In questa fase è indubbiamente utile un righello; se hai deciso che ogni centimetro della carta millimetrata rappresenta 40 km/h e che ogni quadretto da 1 mm è pari a 4 km/h, significa che il vettore è una linea lunga 8 cm (o 80 quadretti).
- Se necessario, usa un goniometro per indicare l'angolo o la direzione del vettore; se questo indica il movimento di un oggetto in direzione nordest, devi tracciare un angolo di 45° rispetto all'orizzonte.
- La direzione del vettore può indicare diversi tipi di misurazioni. Se stai trattando di viaggi, potrebbe riferirsi al percorso lungo la mappa. L'angolo del vettore potrebbe descrivere l'inclinazione rispetto al suolo della traiettoria percorsa da un oggetto lanciato o colpito; in fisica nucleare si utilizza per definire la direzione di un elettrone.
-
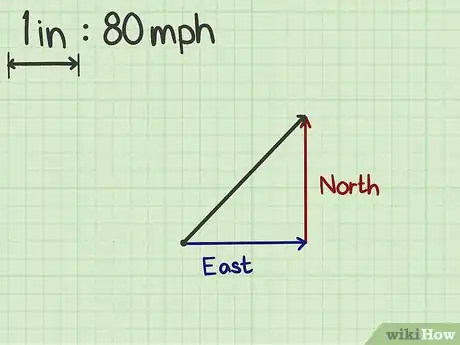
3Disegna un triangolo rettangolo la cui ipotenusa è il vettore. Inizia dalla coda del vettore e traccia un segmento orizzontale lungo quanto basta per allinearsi sotto la punta del vettore. Traccia una punta a freccia alla fine di questo segmento per indicare che è una componente del vettore in esame; disegna quindi un segmento verticale partendo dalla punta del vettore originale senza dimenticare di apporre l'estremità a freccia.[3]
- Dovresti aver realizzato un triangolo rettangolo composto da tre vettori. Quello originale forma l'ipotenusa, quello orizzontale rappresenta la base e quello verticale l'altezza.
- Esistono due eccezioni che non permettono di costruire un triangolo rettangolo: quando il vettore originale è perfettamente orizzontale o verticale; nel primo caso la componente verticale è nulla, nel secondo è nulla la componente orizzontale.
-
4Etichetta le due componenti. In base alla grandezza fisica rappresentata dal vettore originale, dovresti completare il grafico con alcune informazioni. Per esempio, se il vettore rappresenta uno spostamento in direzione nordest, la componente orizzontale indica l'est e quella verticale il nord.[4]
- In altri casi, le componenti potrebbero essere indicate con le etichette "su/giù" oppure "sinistra/destra".
-
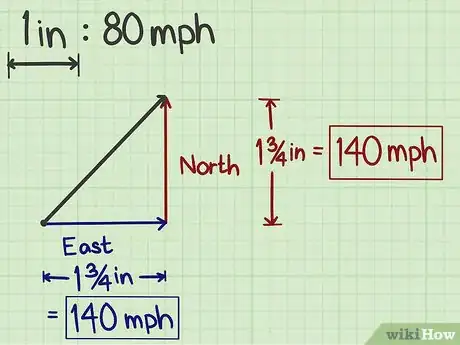
5Misura le componenti. Per determinarne la magnitudine puoi usare la sola carta millimetrata oppure il righello. Se opti per questa seconda soluzione, misura la lunghezza di ciascuna componente vettoriale e trasforma il dato sfruttando la scala che hai scelto all'inizio. Per esempio, se la freccia orizzontale è lunga 4 cm, usando la scala per cui 1 cm = 40 km/h, puoi affermare che la componente est è pari a 160 km/h.[5]
- Se ti affidi alla carta millimetrata invece che al righello, devi procedere con una stima. Se il segmento occupa tre grandi quadrati (ciascuno da 1 cm) e metà del quarto, devi valutare la porzione di quest'ultimo e moltiplicare il tutto per il fattore di scala. Per esempio, 1 quadrato grande corrisponde a 40 km/h e hai valutato che il vettore è lungo 3,5 quadrati; di conseguenza il vettore rappresenta 140 km/h.
- Esegui queste misurazioni sulla componente verticale e orizzontale scrivendo i risultati vicino a ogni vettore.
Pubblicità
Per Via Trigonometrica
-
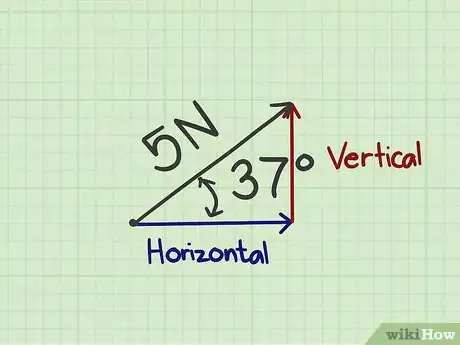
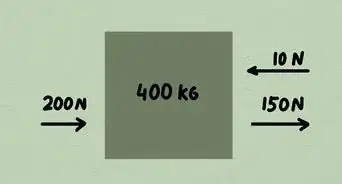
1Disegna un grafico approssimativo del vettore originale. Poiché ti affidi ai calcoli matematici, la rappresentazione grafica non deve essere estremamente precisa: non hai bisogno di definire una scala, ma solamente di tracciare una freccia che indichi la direzione della grandezza fisica. Aggiungi un'etichetta che riporti il modulo e l'angolo rispetto al piano orizzontale.[6]
- Per esempio, considera un razzo che viene lanciato verso l'alto con un angolo di 60° e una velocità di 1500 m/s. Dovresti disegnare una freccia in diagonale rivolta verso l'alto con un'etichetta che riporta "1500 m/s" e un'altra alla base con la scritta "60°".
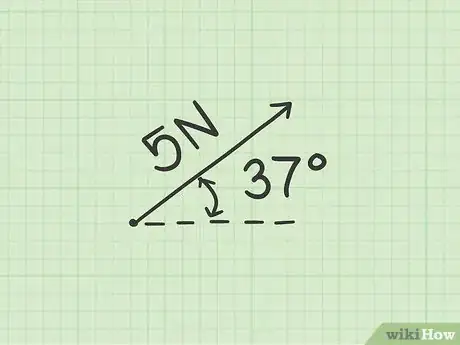
- L'immagine di questo passaggio mostra un vettore con modulo pari a 5 N e un angolo di 37° rispetto al piano orizzontale.
-
2Disegna e definisci le componenti. Traccia una freccia orizzontale che inizia alla base del vettore originale e che punta nella medesima direzione (destra o sinistra); si tratta della componente orizzontale. Disegna ora una freccia verticale che unisce la punta del vettore orizzontale con quella del vettore originale; tale segmento è la componente verticale.[7]
- Le componenti verticali e orizzontali sono una maniera teorica e matematica per scomporre una forza in due parti. Immagina il gioco per bambini "Lavagna magica": un pannello grigio dotato di due pomelli separati per disegnare in verticale e orizzontale. Se tracci una linea usando solamente il pomello verticale e poi usi solamente quello orizzontale, il cursore finisce nello stesso punto in cui si troverebbe se girassi contemporaneamente i pomelli alla medesima velocità. Questo esempio illustra come le componenti verticale e orizzontale di una forza agiscono simultaneamente su un oggetto.
-
3Usa la funzione “seno” per calcolare la componente verticale. Dato che le componenti sono anche i cateti di un triangolo rettangolo, puoi sfruttare i calcoli trigonometrici per ottenere le loro misure esatte. Usa l'equazione:[8]
- ;
- Per quanto riguarda l'esempio del razzo, puoi calcolare la componente verticale inserendo i dati noti e procedendo con le opportune semplificazioni:
- ;
- ;
- ;
- ;
- .
- Apponi le corrette unità di misura; in questo caso, la componente verticale rappresenta una velocità verso l'alto pari a 1299 m/s.
- Il disegno sopra raffigurato mostra un esempio alternativo: la componente verticale di una forza di 5 N applicata con un angolo di 37° rispetto all'orizzonte. Usando la funzione seno si ottiene che tale componente corrisponde a 3 N.
-
4Sfrutta la funzione “coseno” per calcolare la componente orizzontale. Proprio come hai fatto per quella verticale, puoi utilizzare la funzione coseno e calcolare il modulo della componente diretta in orizzontale. Usa questa equazione:[9]
- ;
- Usa i dati relativi all'esempio del razzo per portare a termine i calcoli:
- ;
- ;
- ;
- ;
- .
- Aggiungi le opportune unità di misura. In questo caso la componente orizzontale rappresenta una velocità in avanti (o verso sinistra, destra o all'indietro) di 750 m/s.
- Il diagramma correlato a questo passaggio mostra un altro esempio in cui si calcola la componente orizzontale di una forza di 5 N applicata a 37° rispetto all'orizzonte; usando la funzione coseno si ottiene che tale componente è pari a 4 N.
Pubblicità
Usare le Componenti Vettoriali per Sommare i Vettori
-
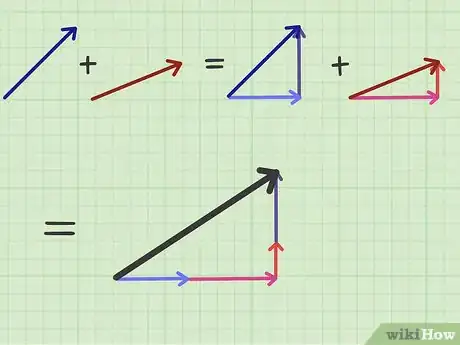
1Comprendi il significato di "somma fra vettori". L'addizione è in genere un concetto semplice, ma quando si parla di vettori assume un significato particolare. Un singolo vettore rappresenta uno spostamento, una forza o un'altra grandezza fisica che agisce su un oggetto; se ci sono due o più forze che agiscono contemporaneamente, puoi "sommarle" e trovare quella risultante che si ripercuote sul corpo.
- Per esempio, considera una pallina da golf che viene colpita e fatta volare. Una forza iniziale è quella impressa dal bastone nel momento in cui la colpisce. Questa è dotata di modulo, direzione e verso. Un'altra forza che potrebbe essere presente è l'azione del vento che possiede una propria direzione e intensità; sommando queste forze tra loro puoi descrivere la traiettoria risultante della pallina.
-
2Scomponi ciascun vettore nelle sue componenti. Prima di poter sommare dei vettori devi determinarne le componenti verticale e orizzontale usando uno dei metodi descritti in precedenza.
- Per esempio, supponi che la pallina da golf venga colpita con un angolo di 30° verso l'alto e le venga impressa una velocità di 130 km/h; usando la trigonometria puoi trovare le due componenti:
- ;
- .
- Ora considera il vettore che descrive l'azione del vento; supponi che spinga la pallina verso il basso con un angolo di 10° e a una velocità di 10 km/h; per il momento ignora altre forze verso destra e sinistra per semplificare i calcoli. Le componenti del vento si possono calcolare nella stessa maniera:
- ;
- .
- Nota che si utilizza un angolo negativo (-10°) perché il vento soffia verso il basso contrastando la forza del colpo.
- Per esempio, supponi che la pallina da golf venga colpita con un angolo di 30° verso l'alto e le venga impressa una velocità di 130 km/h; usando la trigonometria puoi trovare le due componenti:
-
3Somma le componenti. Poiché sono sempre ortogonali fra loro, puoi sommarle direttamente. Ricorda di accoppiare quella verticale di un vettore con la rispettiva verticale dell'altro e di fare lo stesso per quella orizzontale.
- In questo specifico esempio il vettore risultante è la somma delle due componenti:
- ;
- .
- Interpreta il significato dei risultati. La velocità risultante della pallina, tenendo conto del colpo impresso dal giocatore e della resistenza del vento, corrisponde a un vettore la cui componente verticale è pari a 63,25 km/h e quella orizzontale a 122,45 km/h.
- In questo specifico esempio il vettore risultante è la somma delle due componenti:
-
4Sfrutta il teorema di Pitagora per trovare il modulo del vettore finale. Come ultimo passaggio devi trovare la velocità effettiva considerando la spinta del colpo e l'azione del vento; se conosci le due componenti, sommale tra loro rispettando il teorema di Pitagora e individua quindi la magnitudine.
- Ricorda che le componenti sono i cateti di un triangolo rettangolo; il vettore risultante è l'ipotenusa di tale triangolo. Il teorema di Pitagora afferma che: , di conseguenza:
- ;
- ;
- ;
- .
- Il vettore finale rappresenta la velocità della pallina che ha modulo pari a 137,83 km/h; nota che è leggermente maggiore rispetto a quella impressa inizialmente dal giocatore, perché il vento spinge la pallina sia in basso sia in avanti.
- Ricorda che le componenti sono i cateti di un triangolo rettangolo; il vettore risultante è l'ipotenusa di tale triangolo. Il teorema di Pitagora afferma che: , di conseguenza:
-
5Sfrutta la trigonometria per trovare l'angolo risultante del vettore. Conoscere la magnitudine del vettore è solo una parte della soluzione; l'altra metà riguarda la direzione. Nell'esempio considerato la pallina da golf è soggetta alla forza verso l'alto impressa dal giocatore e a quella verso il basso del vento, per quanto inferiore; di conseguenza, devi trovare la direzione risultante.
- Traccia un triangolo rettangolo e poni le relative etichette sulle componenti. La base orizzontale rappresenta il vettore in avanti pari a 122,45 km/h, l'altezza è la componente verticale pari a 63,26 km/h, mentre l'ipotenusa è il vettore finale con modulo di 137,83 km/h.
- Per trovare l'angolo puoi scegliere sia la funzione seno, usando il cateto verticale, sia la funzione coseno (con il cateto orizzontale); il risultato non cambia.
- ;
- ;
- ;
- .
- Il vettore risultante rappresenta quindi la velocità della pallina che viaggia verso l'alto con un angolo di 27,32° rispetto al piano orizzontale. Il risultato è concorde con le aspettative, dato che l'inclinazione è inferiore a quella impressa inizialmente dal giocatore (30°) poiché c'è l'azione del vento diretta verso il basso; tuttavia, il colpo iniziale è molto più intenso della forza del vento e quindi l'angolo della direzione resta prossimo ai 30°.
-
6Riporta la soluzione. Per indicare il vettore risultante devi fornirne il modulo, la direzione e il verso. Per quanto riguarda l'esempio della palla da golf puoi asserire che il vettore che ne rappresenta la velocità finale ha magnitudine pari a 137,83 km/h, una direzione di 27,32° rispetto all'orizzonte e il verso rivolto in alto.Pubblicità
Ripassare i Vettori e le Componenti
-
1Ripassa la definizione di vettore. Si tratta di uno strumento matematico che si utilizza in fisica per rappresentare il modo in cui le forze agiscono su un oggetto. Un vettore indica tre elementi di una forza: la sua intensità, la direzione e il verso con cui viene applicata.[10]
- Per esempio, considerando un oggetto in movimento puoi descrivere il movimento stesso usando la velocità, la direzione e il verso; puoi dire per esempio che un aeroplano viaggia verso nordest a una velocità di 800 km/h. "Nordest" indica sia la direzione sia il verso e 800 km/h il modulo del vettore.
- Un cane condotto al guinzaglio sperimenta una forza vettoriale. Il guinzaglio, tenuto dal padrone, subisce una trazione diagonale rivolta verso l'alto che possiede una certa intensità; l'angolo diagonale è la direzione del vettore e la forza di trazione è il modulo.
-
2Comprendi la terminologia della rappresentazione grafica. Quando disegni un vettore, che si tratti di un grafico molto preciso su carta millimetrata o un semplice abbozzo, devi ovviamente utilizzare determinati termini geometrici.[11]
- Un vettore viene rappresentato graficamente da una . In geometria una freccia è una linea che inizia in un punto ma prosegue, teoricamente, all'infinito in una determinata direzione; viene disegnata tracciando un punto e in seguito un segmento di lunghezza opportuna che termina con una punta a freccia
- La di un vettore è il punto di partenza; geometricamente parlando è il punto terminale della freccia.
- La di un vettore corrisponde all'estremità orientata dotata di freccia. La differenza fra una freccia geometrica e un vettore è che la prima indica un movimento teoricamente all'infinito nella data direzione; il vettore sfrutta invece la freccia per indicare l'orientamento della grandezza fisica e la sua lunghezza termina a livello della punta della freccia stessa. In realtà la freccia di un vettore è un segmento orientato la cui lunghezza indica la magnitudine della forza. In altri termini, se disegni una freccia in geometria la sua lunghezza è irrilevante; se tracci un vettore, la lunghezza è fondamentale.
-
3Ripassa le nozioni basilari di trigonometria. Le componenti di un vettore sfruttano i concetti trigonometrici dei triangoli rettangoli. Ciascun segmento diagonale può essere considerato l'ipotenusa di un triangolo rettangolo disegnando il cateto verticale da un'estremità e quello orizzontale dall'altra; quando questi cateti si intersecano, hai definito un triangolo rettangolo.[12]
- L'angolo di riferimento è quello che l'ipotenusa forma con il cateto orizzontale.
- Il seno dell'angolo di riferimento si trova dividendo la lunghezza del cateto opposto per quella dell'ipotenusa.
- Il coseno dell'angolo di riferimento si calcola dividendo la lunghezza della base (il cateto adiacente) per l'ipotenusa.
Pubblicità
Avvertenze
- Misurare le componenti di un vettore dal grafico è un metodo rapido per trovare dei valori approssimati. Non è una tecnica molto precisa, però, a meno che tu non sia molto bravo nelle misurazioni e nel tracciare il grafico; tuttavia, se ti basta ottenere rapidamente delle stime, può essere la soluzione adatta. Per ottenere dei dati accurati, affidati ai calcoli matematici e trigonometrici.
Riferimenti
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution
- ↑ http://www.physicsclassroom.com/class/vectors/Lesson-1/Vector-Resolution













































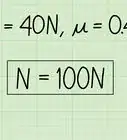

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 24 882 volte