wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 12 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 15 520 volte
Le funzioni esponenziali possono essere usate per rappresentare il tasso di variazione in molti sistemi: per esempio, la crescita demografica, il decadimento radioattivo, la crescita batterica, l’interesse composto e così via. Segui i passaggi descritti di seguito per scrivere un'equazione esponenziale, conoscendo il tasso di crescita o di decadimento della funzione e il valore iniziale del gruppo.
Passaggi
Usa la velocità come base
-
1Vediamo un esempio. Supponiamo che un conto bancario sia aperto con un deposito di $ 1.000 e il tasso d'interesse sia del 3% con capitalizzazione annua. Trova un'equazione esponenziale che rappresenti questa funzione.
-
2Impara la formula base. La formula per un'equazione esponenziale è f(t)=P0(1+r)t/h, dove P0 è il valore iniziale, t è la variabile tempo, r è il tasso di variazione e h è il numero necessario per assicurare che le unità di t siano paragonabili a quelle del tasso di variazione.
-
3Sostituisci P con il valore iniziale e r con il tasso. Otterrai f(t)=1.000(1,03)t/h.
-
4Trova h. Pensa all'equazione. Ogni anno, il denaro aumenta del 3%, il che vuol dire che ogni 12 mesi il denaro aumenta del 3%. Dato che devi dare t in mesi, devi dividere t per 12, quindi h=12. La tua equazione è f(t)=1.000(1,03)t/12. Se l'unità è la stessa per il tasso e per gli aumenti di t, allora h è sempre 1.Pubblicità
Usa "e" come base
-
1Impara cosa rappresenta e. Quando usi il valore e come base, stai usando la "base naturale". L'uso della base naturale ti permette di dedurre il tasso di crescita continua direttamente dall'equazione.
-
2Vediamo un esempio. Supponiamo che 500 grammi di un campione di isotopo di carbonio abbia un tempo di dimezzamento di 50 anni (il tempo di dimezzamento è il tempo necessario per la materia di decadere del 50%).
-
3Impara la formula base. La formula per un'equazione esponenziale è f(t)=aekt, dove a è il valore iniziale, e è la base, k è il tasso di crescita continua, e t è la variabile tempo.
-
4Sostituisci il valore iniziale. L'unico valore assegnato di cui hai bisogno è il tasso di crescita iniziale. Sostituisci quindi a con questo valore e otterrai f(t)=500ekt
-
5Trova il tasso di crescita continua. Il tasso di crescita continuo indica quanto velocemente il grafico cambia in un particolare istante. Sappiamo che tra 50 anni, il campione sarà decaduto a 250 grammi. Questo può essere considerato come un punto sul grafico che può essere inserito. Quindi t è 50. Inseriscilo per ottenere f(50)=500e50k. Sappiamo anche che f(50)=250; sostituisci quindi f(50) con 250 a sinistra dell'uguale e otterrai l'equazione esponenziale 250=500e50k. Per risolvere l'equazione, dividi entrambi i lati per 500: 1/2=e50k. Calcola il logaritmo naturale per entrambi i lati e ottieni: ln(1/2)=ln(e50k). Usa le proprietà dei logaritmi per portare l'esponente fuori dall'argomento del log naturale e moltiplicalo per il log. Il risultato sarà ln(1/2)=50k(ln(e)). Ricorda che ln è lo stesso di loge. Secondo le proprietà dei logaritmi, se la base e l'argomento di un logaritmo sono uguali, il valore è 1. Da qui ln(e)=1. Semplifica l'equazione a ln(1/2)=50k e, dividendo per 50, troverai che k=(ln(1/2))/50. Usando la calcolatrice, trova il valore approssimato di k: -.01386. Nota che questo valore è negativo. Se il tasso di crescita continua è negativo, si tratta di decadimento. Se, invece, è positivo, sarà una crescita esponenziale.
-
6Inserisci il valore di k. L'equazione sarà 500e-.01386t.Pubblicità
Consigli
- Per ottenere dei valori più precisi, potresti memorizzare il valore di k nella tua calcolatrice, anziché usare un'approssimazione al decimale. X è una variabile facilmente accessibile, dato che non devi premere "alfa" per ottenerla. Se vuoi rappresentare l'equazione in un grafico, però, stai attento ad usare una variabile definita come costante, o inserirai delle variabili in più.
- Presto imparerai quali metodi usare. In generale, il primo metodo è più facile. Tuttavia, in altre occasioni, l'uso della base naturale semplificherà i tuoi calcoli in un secondo tempo.

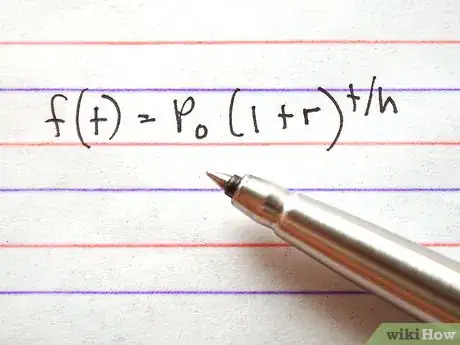
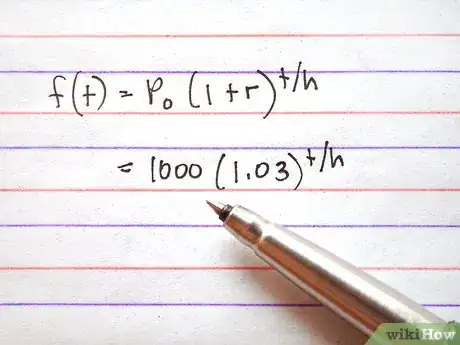
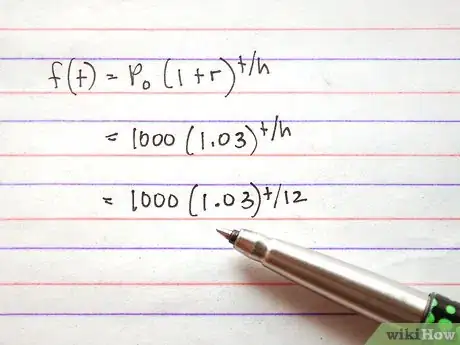




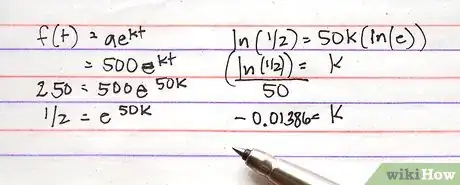

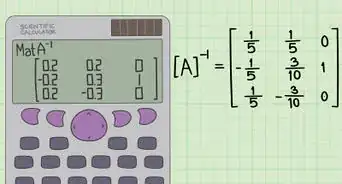




-to-Grams-(g)-Step-12-Version-4.webp)