Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 128 252 volte
In algebra, le operazioni di inversione dei dati vengono usate spesso per semplificare il problema iniziale, che altrimenti risulterebbe molto complesso da risolvere. Ad esempio, se è richiesto di eseguire la divisione con un valore frazionario, è molto più semplice eseguire la moltiplicazione con il relativo reciproco. In questo caso si esegue un'operazione di inversione. Questo concetto si applica molto bene alle matrici, dato che in questo ambito la divisione non è un'operazione valida, quindi si risolve il problema eseguendo una moltiplicazione utilizzando le matrici inverse. Per individuare l'inversa di una matrice 3x3, occorre eseguire manualmente una gran quantità di calcoli, cosa che può sembrare un lavoro noioso, ma che vale la pena effettuare per scoprire i concetti che stanno alla base. In ogni caso, è possibile avvalersi di una calcolatrice grafica con funzionalità avanzate che eseguirà tutto il lavoro in pochi istanti.
Passaggi
Calcolare l'Inversa Usando la Matrice Aggiunta
-
1Controlla il valore del determinante della matrice in esame. Per sapere se la matrice che stai studiando è invertibile, occorre innanzitutto calcolarne il determinate. Se il determinante è pari a 0, significa che il tuo lavoro è già terminato perché la matrice in oggetto non possiede un'inversa. Il determinante di una matrice M si indica con l'espressione matematica det(M).[1]
- Per calcolare il determinante di una matrice 3x3, occorre per prima cosa selezionare una riga o una colonna specifica, calcolare quindi il minore di ciascun elemento della riga o colonna scelta e sommare fra loro i risultati ottenuti rispettandone il segno algebrico.
- Per avere maggiori dettagli su come si calcola il determinante di una matrice, fai riferimento a questo articolo.
-
2Calcola la trasposta della matrice originale. Questo passaggio implica di far ruotare la matrice di 180° lungo la diagonale principale. In altre parole significa invertire gli indici posizionali di ciascun elemento della matrice. Ad esempio, l'elemento che occupa la posizione (i,j) andrà ad occupare la posizione (j,i) e viceversa. Quando si traspongono gli elementi di una matrice, si nota che la diagonale principale (quella che parte dall'angolo superiore sinistro e termina nell'angolo inferiore destro) rimane inalterata.[2]
- È possibile pensare al processo di trasposizione di una matrice come all'operazione che prevede di scambiare le righe con le colonne. La prima riga diventa quindi la prima colonna, la riga centrale diventa la colonna centrale e la terza riga diventa la terza colonna. Osserva l'immagine che correda questo passaggio per capire graficamente come gli elementi della matrice in esame hanno modificato la propria posizione dopo la trasposizione.
-
3Calcola il minore di ciascun elemento della matrice trasposta. Il minore rappresenta il determinante della matrice 2x2 ottenuta dall'eliminazione della riga e della colonna a cui appartiene un elemento specifico. Ogni numero, variabile o espressione presente in una matrice 3x3 è associato a una matrice 2x2 il cui determinante viene chiamato "minore" proprio perché fa riferimento a un insieme più piccolo di dati. Una volta scelto un elemento ed eliminati tutti quelli appartenenti alla stessa riga e colonna, si ottiene una matrice 2x2 di cui calcolare il minore.[3]
- Nell'esempio mostrato nei passaggi precedenti, se si desidera calcolare il minore dell'elemento che si trova sulla seconda riga della prima colonna, occorre eliminare dal calcolo tutti gli elementi che fanno parte della prima colonna e della seconda riga della matrice. Il determinante della matrice 2x2 rimasta rappresenta il minore dell'elemento scelto.
- Calcola il minore di ogni elemento appartenente alla riga o alla colonna selezionata eseguendo le operazioni e i calcoli mostrati finora in questa sezione dell'articolo.
- Per avere maggiori informazioni su come gestire le matrici 2x2, fai riferimento a questo articolo.
-
4Crea la matrice dei cofattori (conosciuta anche come matrice dei complementi algebrici). Posiziona i risultati ottenuti nel passaggio precedente all'interno di una nuova matrice, detta dei cofattori, inserendo il minore di ciascun elemento nella relativa posizione della matrice originale. Ad esempio il minore dell'elemento (1,1) della matrice originale andrà posto nella medesima posizione della matrice dei cofattori. A questo punto, modifica il segno algebrico di ciascun elemento della nuova matrice moltiplicandolo per il segno riportato nella medesima posizione della matrice di riferimento che trovi all'interno della figura a corredo del passaggio.[4]
- Quando si esegue questa operazione, il primo elemento della prima riga della matrice mantiene il suo segno originale, il secondo elemento avrà il segno invertito mentre il terzo manterrà nuovamente il suo segno originale. Continua a elaborare il resto degli elementi delle righe successive utilizzando questo schema. Nota che i segni "+" e "-", che trovi nella matrice di riferimento, non indicano il segno algebrico che dovrà avere il relativo elemento della matrice dei cofattori, ma semplicemente che il relativo elemento dovrà avere il segno invertito (indicato dal simbolo "-") o mantenere quello originale (indicato dal simbolo "+").
- Per avere maggiori informazioni su come ottenere la matrice di cofattori di una matrice data, consulta questo articolo.
- La matrice risultante da questo passaggio viene chiamata matrice aggiunta della matrice originale. La matrice aggiunta si indica con l'espressione matematica agg(M).
-
5Dividi ogni elemento della matrice aggiunta per il determinate. Quest'ultimo è il determinate della matrice M di partenza che abbiamo calcolato nei primi passaggi per scoprire se era possibile invertirla. Dividi ogni valore della matrice aggiunta per il determinante. Posiziona il risultato ottenuto da ogni calcolo al posto del relativo elemento della matrice aggiunta. La nuova matrice risultante rappresenta l'inversa della matrice M originale.[5]
- Ad esempio, il determinante della matrice di riferimento per questa sezione, mostrata nelle relative immagini, è pari a 1. Dividere ogni elemento della matrice aggiunta per il determinate darà quindi come risultato la matrice aggiunta stessa (in questo caso siamo stati fortunati, ma non è sempre così purtroppo).
- Relativamente a quest'ultimo passaggio, anziché eseguire la divisione, altre fonti moltiplicano ogni elemento della matrice aggiunta per l'inverso del determinante della matrice originale, cioè 1/det(M). Matematicamente parlando, le due operazioni sono equivalenti.
Pubblicità
Individuare la Matrice Inversa tramite la Riduzione per Righe
-
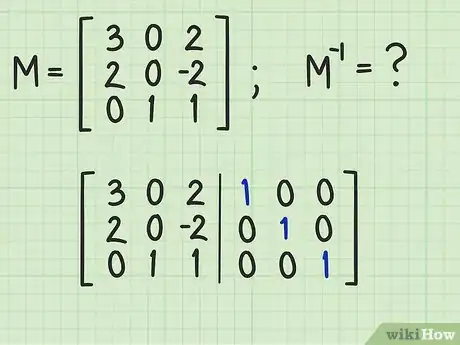
1Aggiungi la matrice identità alla matrice originale. Prendi nota della matrice originale, traccia una linea verticale di separazione sulla sua destra, quindi riporta la matrice identità sulla destra della linea appena tracciata. Adesso dovresti avere una matrice composta da 3 righe e 6 colonne.[6]
- Ricorda che la matrice identità è una matrice speciale, composta da elementi che assumono il valore 1 disposti lungo tutta la diagonale principale e da elementi che assumo il valore 0 in tutte le altre posizioni. Esegui una ricerca online per avere maggiori informazioni riguardanti la matrice identità e le sue proprietà.
-
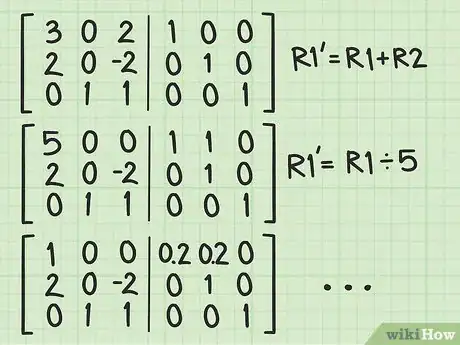
2Esegui la riduzione per righe della nuova matrice ottenuta. L'obiettivo è riuscire a spostare la matrice identità dal lato destro al lato sinistro della nuova matrice. Eseguendo le operazioni inerenti alla riduzione per righe sulla parte sinistra della matrice, dovrai obbligatoriamente applicarle anche al lato destro, in modo che inizi ad assumere la forma di una matrice identità.[7]
- Ricorda che la riduzione per righe di una matrice si esegue tramite una combinazione di moltiplicazioni scalari e di addizioni o sottrazioni allo scopo di portare a 0 gli elementi che si trovano al di sotto della diagonale principale della matrice di riferimento. Per ottenere informazioni più dettagliate su come eseguire la riduzione per righe di una matrice, esegui una ricerca nel web.
-
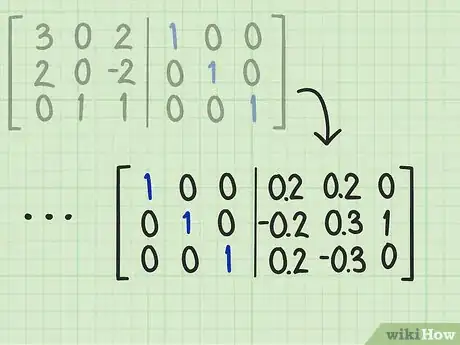
3Prosegui nei calcoli finché non ottieni una matrice identità sul lato sinistro della matrice di partenza. Prosegui eseguendo le operazioni matematiche richieste per ridurre la matrice di partenza finché il lato sinistro non rispecchierà esattamente la matrice identità (composta da 1 sulla diagonale principale e da 0 in tutte le altre posizioni). Una volta raggiunto l'obiettivo, sul lato destro della linea verticale di separazione, avrai esattamente l'inversa della matrice originale.[8]
-
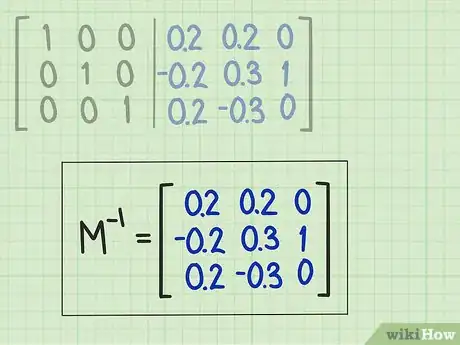
4Prendi nota della matrice inversa. Copia tutti gli elementi che appaiono sul lato destro della linea verticale di separazione della matrice di partenza all'interno della matrice inversa.[9]Pubblicità
Usare una Calcolatrice per Individuare la Matrice Inversa
-
1Scegli un modello di calcolatrice in grado di elaborare le matrici. Le normali calcolatrici utilizzate per svolgere le 4 operazioni matematiche fondamentali non ti saranno di aiuto per questo metodo. In questo caso occorre utilizzare una calcolatrice scientifica con funzionalità grafiche avanzate, come ad esempio la Texas Instruments TI-83 o TI-86, che sono in grado di ridurre enormemente il tuo carico di lavoro.[10]
-
2Inserisci i valori degli elementi della matrice all'interno della calcolatrice. Se la tua calcolatrice ne è dotata, premi il pulsante "Matrix" per attivare la modalità di calcolo relativa alla gestione delle matrici. Se stai utilizzando una calcolatrice prodotta dalla Texas Instruments, devi premere la combinazione di tasti "2nd" e "Matrix".
-
3Accedi al menu secondario "Edit". Per raggiungere questo menu, potresti dover utilizzare i tasti direzionali o scegliere la combinazione di tasti funzione appropriata, in base alla marca e al modello della calcolatrice in uso.[11]
-
4Scegli una delle matrici disponibili. La maggior parte delle calcolatrici è progettata per gestire da 3 a 10 matrici, etichettate rispettivamente con le lettere dell'alfabeto inglese dalla A alla J. Normalmente, per semplicità, si sceglie di utilizzare la matrice [A]. Dopo aver eseguito la selezione, premi il tasto "Enter".[12]
-
5Inserisci le dimensioni della matrice da elaborare. In questo articolo ci focalizziamo sulle matrici 3x3. Tuttavia una normale calcolatrice grafica è in grado di gestire anche matrici molto più grandi. Digita il numero di righe di cui è composta la matrice, quindi premi il tasto "Enter", dopodiché digita il numero di colonne e premi nuovamente il tasto "Enter".[13]
-
6Inserisci gli elementi che compongono la matrice. Sullo schermo della calcolatrice verrà visualizzata una matrice. Se in precedenza hai già utilizzato la funzione "Matrix" del dispositivo, sullo schermo verrà visualizzata l'ultima matrice con cui hai lavorato. Il cursore è posizionato sul primo elemento della matrice. Inserisci il valore degli elementi della matrice su cui devi lavorare, quindi premi il tasto "Enter". Il cursore si sposterà automaticamente sull'elemento successivo da digitare, sovrascrivendone il valore precedente nel caso tu abbia già usato la calcolatrice per lavorare con le matrici in passato.[14]
- Se hai la necessità di inserire un valore negativo, devi premere il pulsante relativo al segno negativo ("-") e non quello relativo alla sottrazione matematica.
- Per spostare il cursore all'interno della matrice, puoi utilizzare i tasti direzionali del dispositivo.
-
7Esci dalla modalità di funzionamento "Matrix". Dopo aver digitato tutti i valori degli elementi che compongono la matrice, premi il tasto "Quit" (oppure usa la combinazione di tasti "2nd" e "Quit"). In questo modo la funzionalità "Matrix" verrà disattivata e a video apparirà la schermata principale della calcolatrice.[15]
-
8Per trovare la matrice inversa, premi l'apposito tasto della calcolatrice. Per prima cosa, occorre selezionare la matrice con cui si desidera lavorare, quindi dovrai attivare nuovamente la modalità "Matrix" e scegliere il nome della matrice che hai utilizzato per inserire i dati di quella su cui stai lavorando (molto probabilmente sarà la matrice [A]). A questo punto, premi il tasto per calcolare la matrice inversa, . In alcuni casi dovrai premere prima il tasto per attivare la seconda funzione, "2nd", in base al modello di calcolatrice in uso. Sullo schermo del dispositivo dovrebbe apparire la dicitura . Premendo il tasto "Enter", sullo schermo dovrebbe apparire l'inversa della matrice inserita.[16]
- Non utilizzare il tasto "^" della calcolatrice nel tentativo di digitare il comando "A^-1". Si tratta pur sempre di una semplice calcolatrice scientifica, che non comprende comandi speciali all'infuori di quelli programmati e preinstallati dal costruttore.
- Se dopo aver premuto il tasto di inversione dovesse apparire un messaggio di errore, è molto probabile che la matrice inserite non abbia un'inversa. Per verificare questa evenienza, dovrai calcolare il relativo determinante.
-
9Converti la matrice inversa ottenuta nella forma corretta. La calcolatrice mostrerà gli elementi della matrice sotto forma di numeri decimali. Nella maggior parte degli ambiti matematici questa forma non è considerata "corretta". Se necessario, dovrai quindi convertire tutti i valori in numeri frazionari. In casi molto rari, e molto fortunati, tutti gli elementi della matrice appariranno sotto forma di numeri interi.[17]
- È molto probabile che la calcolatrice sia dotata di una funzione in grado di convertire automaticamente i numeri decimali in frazioni. Ad esempio, se stai utilizzando la calcolatrice Texas Instruments TI-86, attiva la funzione "Math", accedi al menu "Misc", scegli la funzione "Frac" e infine premi il tasto "Enter". I numeri decimali verranno automaticamente convertiti in frazioni.
Pubblicità
Consigli
- È possibile utilizzare i passaggi descritti in questo articolo anche per calcolare l'inversa di una matrice che contiene numeri, variabili, dati di natura sconosciuta o espressioni algebriche.
- Esegui i calcoli in forma scritta, dato che calcolare l'inversa di una matrice 3x3 a mente è un'operazione estremamente complessa.
- I programmi esistenti sono in grado di calcolare istantaneamente l'inversa di matrici molto grandi con una dimensione fino a 30x30.[18] .
- Verifica sempre che i risultati ottenuti siano corretti, indipendentemente dal metodo utilizzato. Per farlo, moltiplica la matrice originale per la matrice inversa (M x M-1). Controlla che la seguente espressione sia vera: M * M-1 = M-1 * M = I. I rappresenta la matrice identità che è composta da elementi di valore pari a 1 lungo la diagonale principale e da elementi pari a 0 in tutte le altre posizioni. Se ottieni un risultato differente, significa che hai eseguito degli errori di calcolo in qualche passaggio.
Avvertenze
- Ricorda che non tutte le matrici 3x3 sono invertibili. Se il determinante di una matrice di questo tipo è pari a 0, significa che non esiste una sua matrice inversa (nota che nelle formule si esegue la divisione per il determinante della matrice in esame e, come ben sai, in matematica non è possibile dividere un numero per 0).
Riferimenti
- ↑ https://www.mathsisfun.com/algebra/matrix-inverse-minors-cofactors-adjugate.html
- ↑ http://www.mathcentre.ac.uk/resources/uploaded/sigma-matrices11-2009-1.pdf
- ↑ http://www.mathwords.com/c/cofactor_matrix.htm
- ↑ http://www.mathwords.com/c/cofactor_matrix.htm
- ↑ http://mathworld.wolfram.com/MatrixInverse.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ https://people.richland.edu/james/lecture/m116/matrices/inverses.html
- ↑ http://www.bluebit.gr/matrix-calculator/
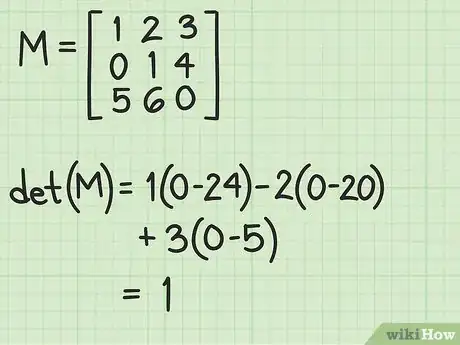
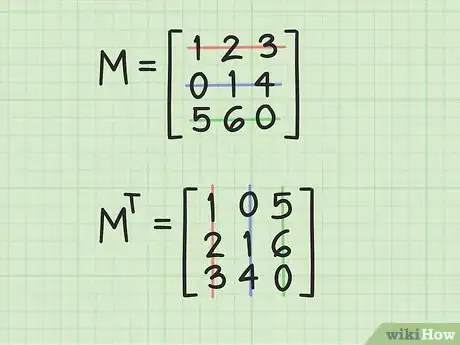

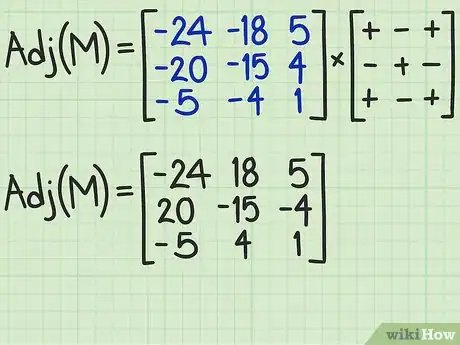
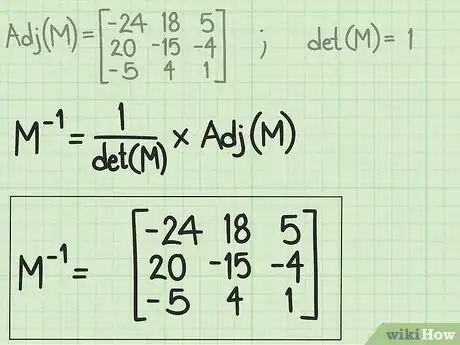














-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 128 252 volte