wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 60 710 volte
Nella maggior parte dei casi, agli studenti di matematica viene richiesto di esprimere la soluzione di un problema in "termini minimi"; in altre parole, di scrivere la risposta nel modo più elegante possibile. Sebbene una lunga e sgraziata espressione sia del tutto equivalente a una breve e bella da vedere, il problema non è considerato "risolto" finché la soluzione non viene espressa in termini minimi. Inoltre, le risposte in termini minimi sono anche delle espressioni semplici da "manipolare". Per tutte queste ragioni, è fondamentale imparare a semplificare le espressioni, se vuoi aspirare a una carriera di matematico.
Passaggi
Criterio d'Ordine delle Operazioni
-
1Impara l'ordine delle operazioni. Quando si semplificano le espressioni, non puoi procedere semplicemente da sinistra verso destra, moltiplicando, sommando e sottraendo i numeri man mano che si presentano. Alcune operazioni matematiche hanno la precedenza sulle altre e devono essere svolte per prime. Se non segui questo criterio, la soluzione che ottieni sarà scorretta. L'ordine delle operazioni è: termini fra parentesi, potenze, moltiplicazioni, divisioni, somme e infine sottrazioni. Ricorda l'acronimo "PEMDAS" che ti aiuta a memorizzare l'esatto ordine.
- Nota che, sebbene la conoscenza base di questo criterio sia utile per risolvere le espressioni elementari, saranno necessarie delle tecniche più avanzate per ridurre ai minimi termini quelle più complesse, fra cui le polinomiali. Leggi il metodo successivo per questo tipo di espressioni.
-
2Comincia risolvendo le operazioni fra parentesi. In matematica le parentesi indicano dei termini che devono essere considerati separatamente dal resto dell'espressione. A prescindere dalle operazioni che dovrai svolgere all'interno di esse, sappi che queste hanno la priorità durante le procedure di semplificazione. Ricordati che all'interno di ogni coppia di parentesi devi comunque rispettare l'ordine delle operazioni e devi sempre moltiplicare prima di sottrarre e così via.
- Per esempio, supponiamo di dover semplificare l'espressione: 2x + 4(5 + 2) + 32 - (3 + 4/2). In questa espressione dobbiamo prima risolvere le operazioni fra parentesi: 5 + 2 e 3 + 4/2. 5 + 2 = 7. 3 + 4/2 = 3 + 2 = 5.
- I termini nella seconda parentesi vengono semplificati a 5 perché, seguendo l'ordine delle operazioni, per prima cosa si risolve la divisione 4/2. Se avessimo semplicemente seguito la successione dei numeri come si presentano da sinistra a destra, avremmo prima sommato 3 con 4 e poi diviso il risultato per 2 ottenendo 7/2, una soluzione sbagliata.
- Nota: se ci sono più parentesi le une nelle altre, risolvi prima la più interna e procedi verso l'esterno.
- Per esempio, supponiamo di dover semplificare l'espressione: 2x + 4(5 + 2) + 32 - (3 + 4/2). In questa espressione dobbiamo prima risolvere le operazioni fra parentesi: 5 + 2 e 3 + 4/2. 5 + 2 = 7. 3 + 4/2 = 3 + 2 = 5.
-
3Risolvi le potenze. Dopo avere affrontato le parentesi, passa alle potenze. Non sono difficili da identificare perché la base e l'esponente sono scritti vicini fra loro con il secondo posizionato nell'angolo in alto a destra del primo. Risolvi ogni potenza e scrivine il risultato sostituendolo all'interno dell'espressione.
- Dopo avere risolto le operazioni fra parentesi, la nostra espressione dell'esempio precedente si presenta come: 2x + 4(7) + 32 - 5. L'unica potenza presente è 32 che equivale a 9. Sostituiamo questo valore all'interno della potenza e otteniamo: 2x + 4(7) + 9 - 5.
-
4Risolvi le moltiplicazioni. A questo punto devi affrontare le moltiplicazioni. Ricorda che questa operazione può essere scritta in molti modi. A volte si usa il simbolo “x”, un punto o un asterisco per intendere la moltiplicazione. Tuttavia anche un numero vicino a una coppia di parentesi o a una variabile (come 4(x)) denota una moltiplicazione.
- Nel nostro problema ci sono due moltiplicazioni: 2x (2x significa 2 volte x) e 4(7). Non conosciamo il valore di x, quindi 2x viene trascritto tale e quale, mentre 4(7) = 4 x 7 = 28. Possiamo riscrivere la nostra espressione come: 2x + 28 + 9 - 5.
-
5Passa alle divisioni. Proprio come le moltiplicazioni, anche le divisioni possono essere scritte con molti simboli diversi. Il semplice segno “:” ne è un esempio, ma ricordati che anche la barra diagonale (/) e la frazione (come 3/4 per esempio) sono sinonimo di divisione.
- Poiché abbiamo già risolto la divisione (4/2) che era racchiusa nelle parentesi, la nostra espressione non presenta altre divisioni e quindi possiamo saltare questo passaggio. Questo ci porta a sottolineare un aspetto fondamentale: quando semplifichi le espressioni non è detto che tu debba eseguire tutte le operazioni dell'acronimo PEMDAS, ma solo quelle che sono effettivamente presenti nel problema.
-
6Risolvi le somme. A questo punto puoi affrontare tutte le operazioni di somma presenti nell'espressione, ma per prima cosa, è opportuno riordinare gli addendi in modo che siano semplici da gestire. Ad esempio l'espressione 49 + 29 + 51 +71, è più semplice da risolvere se vista come 49 + 51 = 100, 29 + 71 = 100 e quindi 100 + 100 = 200, piuttosto che come 49 + 29 = 78, 78 + 51 = 129 e 129 + 71 = 200.
- L'espressione del nostro esempio è parzialmente semplificata e abbiamo: "2x + 28 + 9 - 5". Ora dobbiamo passare alle addizioni e analizziamo il problema da sinistra verso destra. Non possiamo sommare fra loro 2x e 28 perché non conosciamo il valore di x, quindi andiamo oltre. 28 + 9 = 37, quindi trascriviamo il risultato nell'espressione: "2x + 37 - 5".
-
7Esegui le sottrazioni. Questo è l'ultimo passaggio dell'ordine PEMDAS. Analizza il tuo problema e risolvi tutte le sottrazioni che incontri. Potresti imbatterti in numeri negativi durante questa fase e, come nel passaggio di una normale addizione, non influiranno sulla risposta finale.
- Consideriamo sempre il nostro esempio: "2x + 37 - 5", dove c'è una sola sottrazione da risolvere: 37 - 5 = 32
-
8Controlla l'espressione. Dopo aver superato tutti i passaggi previsti dal criterio di ordine delle operazioni, l'espressione dovrebbe essere risolta ai minimi termini. Tuttavia, se il problema contiene una o più variabili, sappi che queste, nella maggioranza dei casi, non verranno modificate. Semplificare delle espressioni con delle variabili richiede la capacità di trovare il valore di queste o di utilizzare delle tecniche specifiche (affrontate nella sezione successiva).
- La nostra soluzione finale per l'espressione è "2x + 32". Non potremo semplificare ulteriormente il risultato finché non conosciamo il valore di x e, in tal caso, si tratterebbe comunque di un calcolo decisamente più semplice rispetto a quello proposto dalla lunga espressione iniziale.
Pubblicità
Espressioni Complesse
-
1Somma fra loro le variabili simili. Quando devi affrontare delle espressioni con variabili, è importante che i termini che presentano medesima variabile ed esponente (detti "simili") possano essere sommati e sottratti fra loro come normali numeri. Questi termini devono avere non solo la stessa variabile, ma anche il medesimo esponente. Per esempio, 7x e 5x possono essere sommati fra loro ma 7x e 5x2 no.
- Questa regola si estende anche a quei monomi con più variabili. Ad esempio, 2xy2 può essere sommato a -3xy2 ma non a -3x2y o -3y2.
- Osserviamo l'espressione: x2 + 3x + 6 - 8x. Possiamo sommare 3x e -8x perché sono simili fra loro. In tal caso il problema diventa x2 - 5x + 6.
-
2Semplifica i numeri frazionali dividendo i fattori. Le frazioni fra soli numeri (senza variabili) possono essere semplificate in molti modi. Il primo, e forse il più semplice, consiste nel risolvere la divisione che è implicita nella frazione stessa. Inoltre, ogni fattore che compare sia al denominatore che al numeratore può essere "cancellato" dato che il rapporto è pari a uno. In altre parole, se il numeratore e il denominatore hanno un fattore comune, questo può essere eliminato per semplificare il risultato.
- Per esempio consideriamo la frazione 36/60. Se avessimo una calcolatrice potremmo procedere alla semplice divisione e ottenere il risultato 0,6. Tuttavia svolgiamo i calcoli a mano e semplifichiamo i fattori comuni. Infatti possiamo ripensare la frazione 36/60 come (6 × 6)/(6 × 10). Questo ci permette di riscriverla come: 6/6 × 6/10. Dato che 6/6 = 1, l'espressione può essere semplificata a 6/10.Questo non è sufficiente perché sia 6 che 10 presentano il fattore 2. Se ripetiamo la procedura di prima otteniamo 3/5.
-
3In una frazione con variabili possiamo cancellare le variabili comuni. Infatti, le espressioni variabili che sono espresse come frazione hanno una sola opportunità di semplificazione. Proprio come i normali numeri frazionali, puoi rimuovere i fattori comuni fra denominatore e numeratore, con l'unica differenza che questi fattori possono essere dei numeri e delle lettere.
- Prendiamo in esame l'espressione (3x2 + 3x)/(-3x2 + 15x).Questa frazione può essere riscritta come (x + 1)(3x)/(3x)(5 - x); 3x compare sia al numeratore che al denominatore e può essere cancellato. Questo conduce a una forma semplificata pari a (x + 1)/(5 - x). Allo stesso modo, nel problema (2x2 + 4x + 6)/2, dato che tutti i termini sono divisibili per 2, possiamo riscriverlo come (2(x2 + 2x + 3))/2, che può essere ulteriormente semplificato a x2 + 2x + 3.
- Nota che non puoi cancellare tutti i termini in maniera indiscriminata ma solo i fattori comuni fra denominatore e numeratore. Ad esempio nell'espressione (x(x + 2))/x, la "x" si cancella sia dal numeratore sia dal denominatore lasciando (x + 2)/1 = (x + 2). Tuttavia non è possibile fare lo stesso in (x + 2)/x semplificando a 2/1 = 2.
-
4Moltiplica i termini all'interno delle parentesi per le loro costanti. Quando devi affrontare dei termini con delle parentesi adiacenti a delle costanti, a volte vale la pena svolgere le moltiplicazioni per semplificare l'espressione. Questo è vero sia per costanti numeriche che variabili.
- Prendiamo in esame l'espressione: 3(x2 + 8). Questa può essere semplificata in 3x2 + 24, mentre 3x(x2 + 8) può essere riscritta nella forma 3x3 + 24x.
- Nota che, in alcuni casi come con le frazioni variabili, la costante adiacente a una parentesi dà la possibilità di cancellare dei fattori e non andrebbe moltiplicata. Nella frazione (3(x2 + 8))/3x, ad esempio, il fattore 3 appare sia al numeratore che al denominatore, quindi può essere eliminato e si può riscrivere il problema come (x2 + 8)/x. Questo è un metodo più semplice e facile rispetto allo svolgimento della moltiplicazione: (3x3 + 24x)/3x.
-
5Semplifica l'espressione tramite la scomposizione in fattori. La scomposizione è una tecnica tramite la quale si possono semplificare le espressioni con variabili, incluse quelle polinomiali. Pensa alla scomposizione in fattori come l'operazione inversa alla "moltiplicazione fra parentesi" spiegata in precedenza. A volte un'espressione può essere riscritta in maniera più semplice se pensata come a un insieme di fattori moltiplicati fra loro. Questo è particolarmente vero se la scomposizione ti consente di cancellare parte dell'espressione stessa (proprio come accade nelle frazioni). In questi casi speciali (spesso con le equazioni di secondo grado), la scomposizione ti permette di trovare il risultato finale.
- Valutiamo l'espressione x2 - 5x + 6 ancora una volta. Questa può essere scomposta in (x - 3)(x - 2). Quindi se x2 - 5x + 6 fosse il numeratore di una data espressione frazionale con uno dei termini in comune con il denominatore, questa scomposizione ci consentirebbe di eliminare il fattore comune. Ad esempio (x2 - 5x + 6)/(2(x - 2)), può essere riscritta come in (x - 3)(x – 2)/(2(x - 2), cancellando il termine comune (x - 2) otteniamo (x - 3)/2.
- Come suggerito in precedenza, un altro motivo per cui dovresti scomporre in fattori un'espressione è che questo passaggio potrebbe rivelare la soluzione di determinate equazioni, soprattutto quelle poste uguali a zero. Ad esempio analizziamo x2 - 5x + 6 = 0. Se scomponiamo l'espressione in fattori otteniamo che (x - 3)(x - 2) = 0. Poiché qualunque numero moltiplicato per zero dà come prodotto zero, allora possiamo affermare che quando i termini all'interno delle parentesi sono pari a zero, l'equazione è vera. Ciò significa che le soluzioni all'equazione sono 3 e 2.
Pubblicità
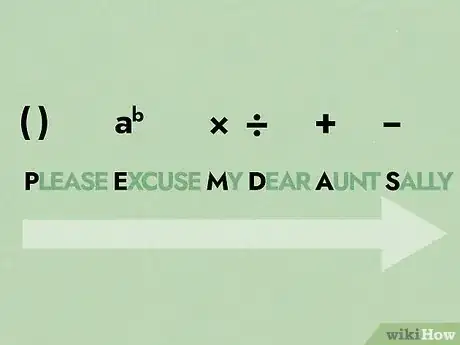







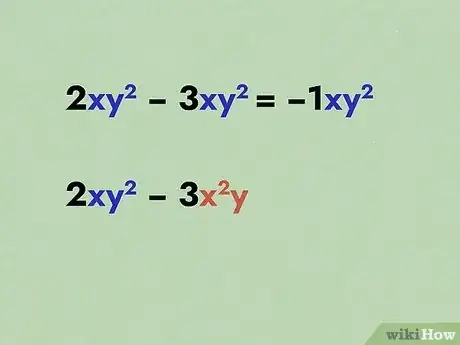
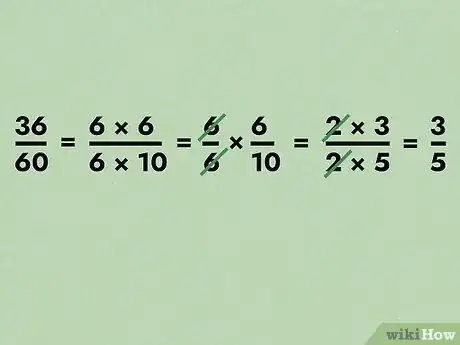
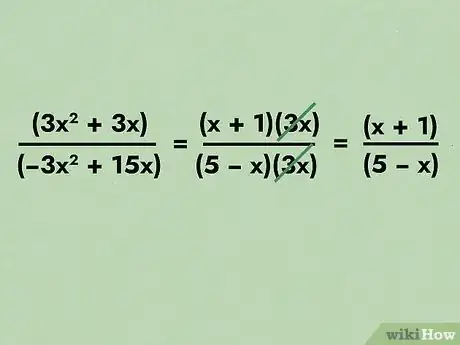
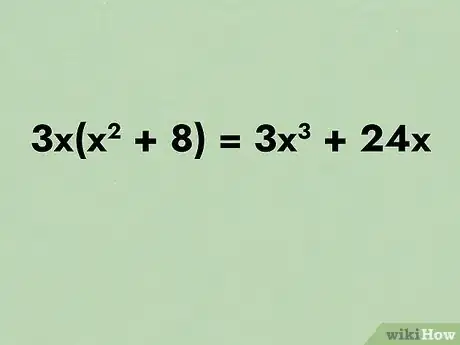
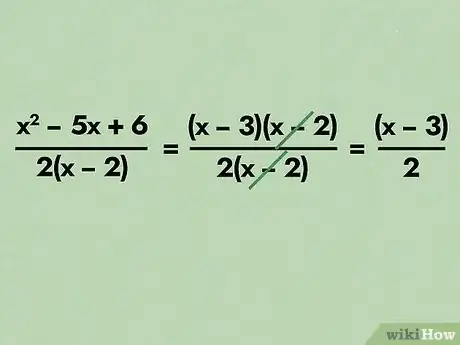




-to-Grams-(g)-Step-12-Version-4.webp)













