X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 11 214 volte
Le espressioni razionali devono essere semplificate al loro fattore minimo. Questo è un procedimento piuttosto semplice se il fattore è un singolo, ma può essere un po’ più complesso se i fattori includono più termini. Ecco cosa devi fare in base al tipo di espressione razionale che devi risolvere.
Passaggi
Metodo 1
Metodo 1 di 3:
Espressione Razionale di Monomi
-
1Valuta il problema. Le espressioni razionali che consistono di soli monomi sono le più semplici da ridurre. Se entrambi i termini dell’espressione hanno un termine ciascuno, tutto ciò che devi fare è di ridurre il numeratore ed il denominatore per il loro massimo comune denominatore.
- Nota che mono significa “uno” o “singolo” in questo contesto.
- Esempio: 4x/8x^2
-
2Cancella le variabili condivise. Guarda le variabili che appaiono nell’espressione, sia al numeratore che al denominatore c’è la stessa lettera, puoi cancellarla dall’espressione rispettando le quantità che ci sono nei due fattori.
- In altre parole, se la variabile appare una volta al numeratore ed una volta al denominatore puoi semplicemente cancellarla poiché: x/x = 1/1 = 1
- Se, al contrario, la variabile appare in entrambi i fattori ma in quantità diverse, sottrai da quella che ha una potenza maggiore, quella che ha la potenza minore: x^4/x^2 = x^2/1
- Esempio: x/x^2 = 1/x
-
3Riduci le costanti ai minimi termini. Se le costanti numeriche hanno un denominatore comune, dividi il numeratore ed il denominatore per questo fattore e riporta la frazione alla forma minima: 8/12 = 2/3
- Se le costanti dell’espressione razionale non hanno un denominatore comune, non può essere semplificata: 7/5
- Se una delle due costanti può dividere l’altra completamente, va considerata come denominatore comune: 3/6 = 1/2
- Esempio: 4/8 = 1/2
-
4Scrivi la tua soluzione. Per determinarla, devi ridurre sia le variabili sia le costanti numeriche e ricombinarle fra loro:
- Esempio: 4x/8x^2 = 1/2x
Pubblicità
Metodo 2
Metodo 2 di 3:
Espressioni Razionali di Binomi e Polinomi con Fattori Monomiali
-
1Valuta il problema. Una parte dell’espressione è monomiale ma l’altra è binomiale o un polinomio. Devi semplificare l’espressione cercando un fattore monomiale che possa essere applicato sia al numeratore che al denominatore.
- In questo contesto, mono significa “uno” o “singolo,” bi significa “due,” e poli significa “più di due.”
- Esempio: (3x)/(3x + 6x^2)
-
2Separa le variabili condivise. Se al numeratore e al denominatore appaiono le stesse variabili, puoi includerle nel fattore di divisione.
- Questo vale solo se le variabili appaiono in ciascun termine dell’espressione: x/(x^3 – x^2 + x) = (x)(1)/ [(x)(x^2 – x + 1)]
- Se un termine non contiene la variabile, non puoi usarla come fattore: x/x^2 + 1
- Esempio: x/(x + x^2) = [(x)(1)] / [(x)(1 + x)]
-
3Separa le costanti numeriche condivise. Se le costanti in ogni termine dell’espressione hanno dei fattori comuni, dividi ogni costante per il divisore comune per ridurre il numeratore ed il denominatore.
- Se una costante divide l’altra completamente, va considerata come divisore comune: 2 / (2 + 4) = 2 * [1 / (1 + 2)]
- Questo vale solo se tutti i termini dell’espressione condividono lo stesso divisore: 9 / (6 – 12) = 3 * [3 / (2 – 4)]
- Non vale se uno qualsiasi dei termini dell’espressione non condivide lo stesso divisore: 5 / (7 + 3)
- Esempio: 3/(3 + 6) = [(3)(1)] / [(3)(1 + 2)]
-
4Porta fuori i valori condivisi. Combina le variabili e le costanti ridotte per determinare il fattore comune. Rimuovi questo fattore dall’espressione lasciando le variabili e le costanti che non possono essere ulteriormente semplificate tra loro.
- Esempio: (3x)/(3x + 6x^2) = [(3x)(1)] / [(3x)(1 + 2x)]
-
5Scrivi la soluzione finale. Per determinarla, rimuovi i fattori comuni.
- Esempio: [(3x)(1)] / [(3x)(1 + x)] = 1/(1 + x)
Pubblicità
Metodo 3
Metodo 3 di 3:
Espressioni Razionali di Binomi e Polinomi con fattori Binomiali
-
1Valuta il problema. Se non ci sono monomi nell’espressione, devi riportare il numeratore ed il denominatore a fattori binomiali.
- In questo contesto, mono significa “uno” o “singolo,” bi significa “due,” e poli significa “più di due.”
- Esempio: (x^2 - 4) / (x^2 - 2x - 8)
-
2Suddividi il numeratore in binomi. Per farlo devi trovare le possibili soluzioni per la variabile x.
-
Esempio: (x^2 – 4) = (x - 2) * (x + 2).
- Per risolvere per x, devi mettere la variabile a sinistra dell’uguale e le costanti a destra dell’uguale:x^2 = 4.
- Riduci la x a potenza singola facendo la radice quadrata: √x^2 = √4.
- Ricorda che la soluzione di una radice quadrata può essere sia negativa che positiva. Quindi le soluzioni possibili per x sono: -2, +2.
- Quindi la suddivisione di (x^2 – 4) nei suoi fattori è: (x - 2) * (x + 2).
- Fai un doppio controllo moltiplicando fra loro i fattori. Se sei incerto sulla correttezza dei tuoi calcoli, fai questa prova; dovresti ritrovare l’espressione originaria.
- Esempio: (x - 2) * (x + 2) = x^2 + 2x - 2x – 4 = x^2 – 4
-
Esempio: (x^2 – 4) = (x - 2) * (x + 2).
-
3Suddividi il denominatore in binomi. Per farlo devi determinare le possibili soluzioni per x.
-
Esempio: (x^2 - 2x – 8) = (x + 2) * (x – 4)
- Per risolvere in x, devi spostare le variabili a sinistra dell’uguale e le costanti a destra: x^2 − 2x = 8
- Aggiungi ad entrambi i lati la radice quadrata della metà del coefficiente della x: x^2 − 2x + 1 = 8 + 1
- Semplifica entrambi i lati: (x − 1)^2 = 9
- Fai la radice quadrata: x − 1 = ±√9
- Risolvi per x: x = 1 ±√9
- Come per tutte le equazioni quadrate, x ha due possibili soluzioni.
- x = 1 - 3 = -2
- x = 1 + 3 = 4
- Quindi i fattori di (x^2 - 2x – 8) sono: (x + 2) * (x – 4)
- Fai un doppio controllo moltiplicando i fattori fra loro. Se non sei sicuro dei tuoi calcoli fai questa prova, dovresti ritrovare l’espressione originaria.
- Esempio: (x + 2) * (x – 4) = x^2 – 4x + 2x – 8 = x^2 - 2x - 8
-
Esempio: (x^2 - 2x – 8) = (x + 2) * (x – 4)
-
4Elimina i fattori comuni. Determina quali binomi, se ce ne sono, sono in comune fra il numeratore ed il denominatore e rimuovili dall’espressione. Lascia quelli che non possono essere semplificati tra loro.
- Esempio: [(x - 2)(x + 2)] / [(x + 2)(x – 4)] = (x + 2) * [(x – 2) / (x – 4)]
-
5Scrivi la soluzione. Per farlo rimuovi i fattori comuni dall’espressione.
- Esempio: (x + 2) * [(x – 2) / (x – 4)] = (x – 2) / (x – 4)
Pubblicità
Cose che ti Serviranno
- Calcolatrice
- Matita
- Carta
Informazioni su questo wikiHow
Pubblicità


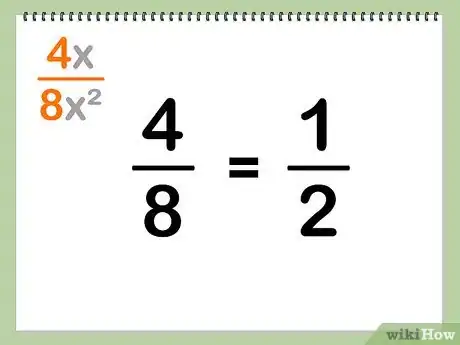
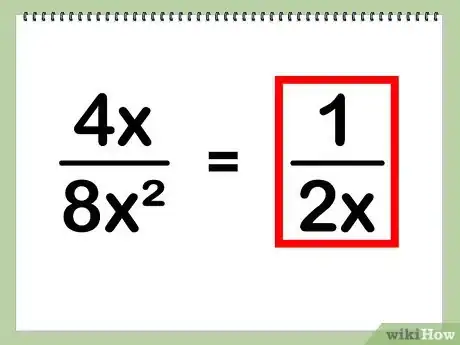

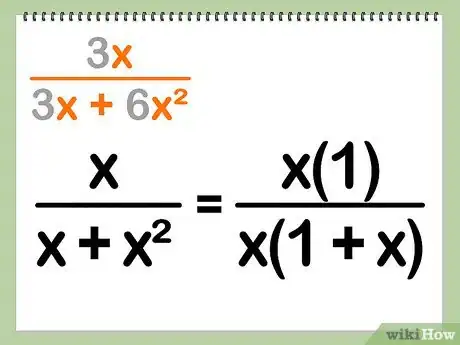

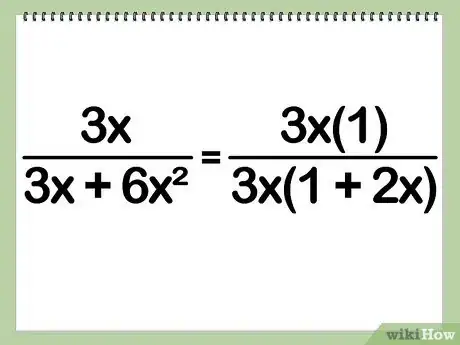




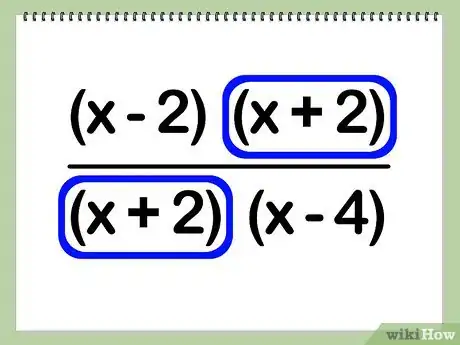
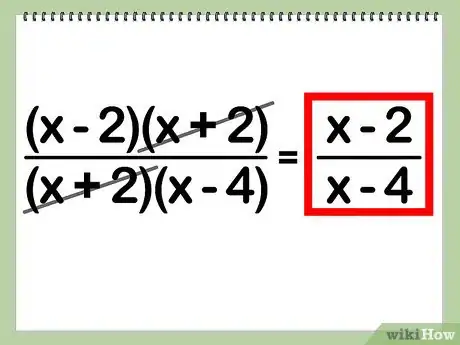



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
