Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 17 724 volte
Puoi sommare una serie di numeri dispari consecutivi[1] a mano, ma c'è un metodo molto più semplice per farlo, specialmente se hai molte cifre da sommare. Una volta imparata una semplice formula, riuscirai a sommare questi numeri molto velocemente senza usare una calcolatrice. Inoltre c'è un modo molto facile per calcolare quali numeri consecutivi danno una specifica somma.
Passaggi
Applicare la Formula per la Sommatoria di una Sequenza di Numeri Dispari Consecutivi
-
1Scegli un punto d'arrivo. Prima di iniziare, devi decidere quale sarà l'ultimo numero consecutivo della serie. Questa formula può aiutarti a sommare una serie qualunque di numeri dispari consecutivi, partendo da 1.[2]
- Se devi svolgere un compito, questo numero ti verrà assegnato. Per esempio, se un problema ti chiede di trovare la somma di tutti i numeri dispari consecutivi tra 1 e 81, il numero finale è 81.
-
2Aggiungi 1. Il passaggio seguente è semplicemente aggiungere 1 al numero finale. Dovresti ottenere un numero pari, fondamentale per il passaggio successivo.
- Per esempio, se il numero finale è 81, 81 + 1 = 82.
-
3Dividi per 2. Una volta ottenuto un numero pari, dovresti dividerlo per 2. Otterrai un valore dispari uguale al numero delle cifre sommate insieme.
- Per esempio, 82 / 2 = 41.
-
4Eleva la somma al quadrato. L'ultimo passaggio è calcolare il quadrato del numero, o moltiplicarlo per se stesso. Una volta fatto, otterrai il risultato.
- Per esempio, 41 x 41 = 1681. Questo significa che la somma di tutti i numeri dispari consecutivi tra 1 e 81 è 1681.
Pubblicità
Comprendere il Funzionamento della Formula
-
1Osserva lo schema che si ripete. Il segreto per comprendere questa formula è riconoscere lo schema che ne sta alla base. La somma di una qualsiasi serie di numeri dispari consecutivi che parte da 1 è sempre uguale al quadrato del numero di cifre sommate insieme.[3]
- Somma del primo numero dispari = 1.
- Somma dei primi due numeri dispari = 1 + 3 = 4 (= 2 x 2).
- Somma dei primi tre numeri dispari = 1 + 3 + 5 = 9 (= 3 x 3).
- Somma dei primi quattro numeri dispari = 1 + 3 + 5 + 7 = 16 (= 4 x 4).
-
2Comprendi i dati parziali. Risolvendo questo problema, hai appreso più della somma dei numeri. Hai anche capito quante cifre consecutive sono state sommate: 41! Questo perché il numero di cifre sommate è sempre uguale alla radice quadrata della somma.
- La somma del primo numero dispari = 1. La radice quadrata di 1 è 1 e solo un numero è stato sommato.
- La somma dei primi due numeri dispari = 1 + 3 = 4. La radice quadrata di 4 è 2 e due cifre sono state sommate.
- La somma dei primi tre numeri dispari = 1 + 3 + 5 = 9. La radice quadrata di 9 è 3 e tre cifre sono state sommate.
- La somma dei primi quattro numeri dispari = 1 + 3 + 5 + 7 = 16. La radice quadrata di 16 è 4 e quattro cifre sono state sommate.
-
3Generalizza la formula. Una volta compresa la formula e il suo funzionamento, puoi scriverla in un formato applicabile a prescindere dai numeri con cui hai a che fare. La formula per calcolare la somma dei primi n numeri dispari è n x n o n al quadrato.
- Per esempio, se sostituisci 41 a n, avresti 41 x 41, o 1681, cioè la somma dei primi 41 numeri dispari.
- Se non sai con quanti numeri hai a che fare, la formula per determinare la somma tra 1 e n è (1/2(n + 1))2.
Pubblicità
Determinare Quali Numeri Dispari Consecutivi Danno una Certa Somma
-
1Impara le differenze tra i due tipi di problemi. Se ti viene assegnata una serie di numeri dispari consecutivi e ti viene chiesto di calcolarne la somma, dovresti usare l'equazione (1/2(n + 1))2. Se invece ti viene assegnata una somma e ti viene chiesto di trovare la serie di numeri dispari consecutivi che la compongono, devi usare una formula diversa.
-
2Eguaglia n al primo numero. Per scoprire quali numeri dispari consecutivi danno una specifica somma, devi creare una formula algebrica. Inizia usando n per rappresentare il primo numero della sequenza.[4]
-
3Scrivi i numeri restanti in relazione a n. Devi determinare come scrivere gli altri numeri della sequenza relativamente a n. Dato che si tratta di numeri dispari consecutivi, tra due numeri successivi la differenza sarà sempre pari a 2.
- Questo significa che il secondo numero della serie sarà n + 2, il terzo n + 4, eccetera.
-
4Completa la formula. Una volta che sai come rappresentare tutti i numeri della serie, è il momento di scrivere la formula. La parte sinistra deve rappresentare i numeri della serie, quella destra la loro somma.
- Per esempio, se ti viene chiesto di trovare una serie di due numeri dispari consecutivi la cui somma è pari a 128, dovresti scrivere n + n + 2 = 128.
-
5Semplifica l'equazione. Se dal lato sinistro è presente più di un termine con n, sommali insieme. In questo modo diventerà molto più semplice risolvere il problema.[5]
- Per esempio, n + n + 2 = 128 si semplifica in 2n + 2 = 128.
-
6Isola n. L'ultimo passaggio per risolvere l'equazione è isolare n da un lato dell'equazione. Ricorda che tutte le modifiche che applichi da un lato dell'equazione devono essere ripetute anche dall'altro lato.
- Risolvi prima addizioni e sottrazioni. In questo caso devi sottrarre 2 da entrambi i lati dell'equazione per ottenere n da sola, quindi 2n = 126.
- Passa alle moltiplicazioni e alle divisioni. In questo caso devi dividere entrambi i lati dell'equazione per 2, se desideri isolare n, quindi n = 63.
-
7Scrivi la risposta. A questo punto sai che n = 63, ma non hai ancora finito. Devi assicurarti di rispondere completamente alla domanda che ti è stata posta. Se ti viene chiesto quale serie di numeri dispari consecutivi dà una certa somma, devi scrivere tutti i numeri che la compongono.
- La risposta a questo problema è 63 e 65, perché n = 63 e n + 2 = 65.
- È sempre una buona idea controllare la soluzione sostituendo i numeri nell'equazione. Se non ottieni la somma desiderata come risultato, prova a rifare i calcoli.
Pubblicità
Riferimenti
- ↑ http://www.aaamath.com/g25a2-evenodd.html
- ↑ http://mathforum.org/k12/mathtips/addconsec.odd.html
- ↑ https://www.khanacademy.org/math/algebra/one-variable-linear-equations/alg1-linear-equations-word-problems/v/sum-consecutive-integers
- ↑ http://www.mathsteacher.com.au/year10/ch02_linear_equations/06_consecutive_numbers/cons.htm
- ↑ https://www.mathsisfun.com/algebra/simplify.html

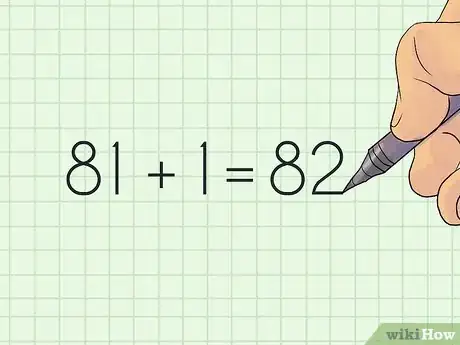
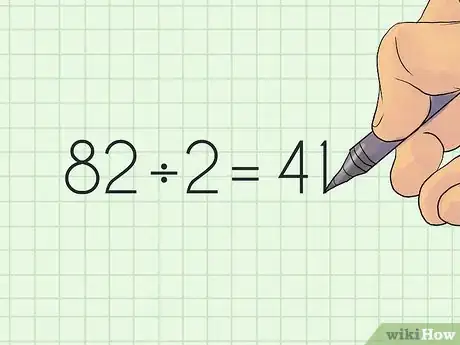
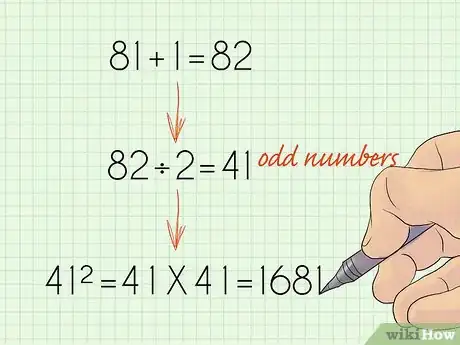
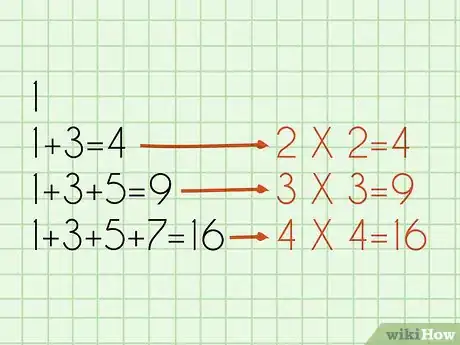
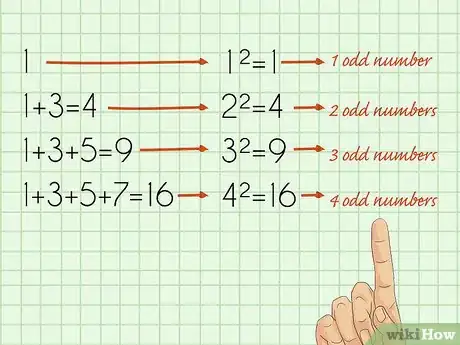
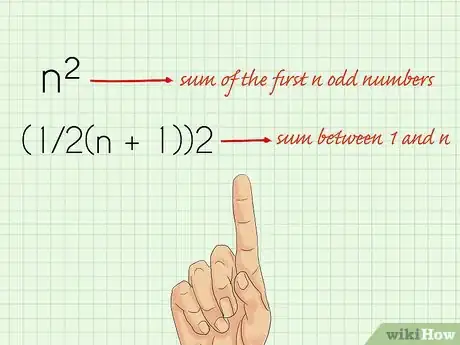




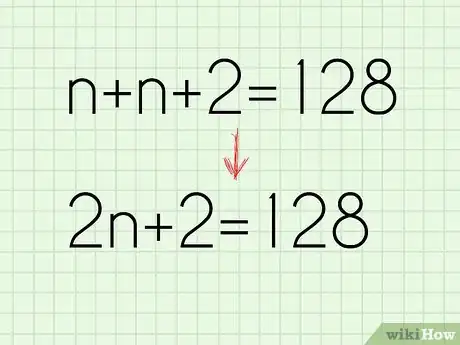

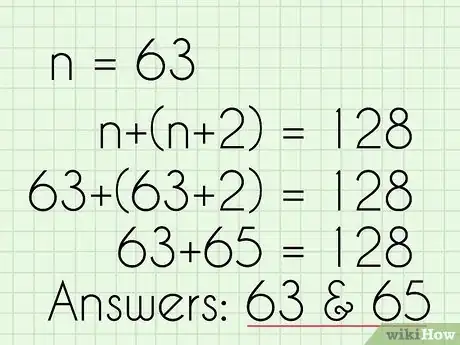



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 17 724 volte