wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 18 164 volte
Tracciare il grafico delle equazioni è un processo molto più semplice di quanto si possa credere. Non devi essere un genio della matematica o un "secchione" per impararne le basi senza il supporto di una calcolatrice. Apprendi alcuni di questi metodi per disegnare il grafico di equazioni lineari, di secondo grado, con valore assoluto e disequazioni.
Passaggi
Equazioni Lineari
-
1Usa la formula y=mx+b. Tutto quello che devi fare per disegnare il grafico di un'equazione lineare è sostituire le variabili di questa formula.
- In questo caso devi risolvere l'equazione per (x,y).
- Il coefficiente "m" corrisponde alla pendenza o al coefficiente angolare, cioè il rapporto tra il sollevamento e il percorso orizzontale.
- Nella formula, b è l'intercetta verticale e corrisponde al punto di intersezione fra l'asse delle ordinate e la retta definita dall'equazione.
-
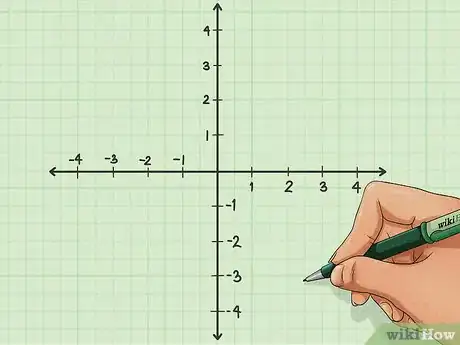
2Traccia il grafico. Il caso di un'equazione lineare è il più semplice, dato che non devi calcolare alcun numero prima di iniziare. Disegna le coordinate cartesiane sul piano di riferimento.
-
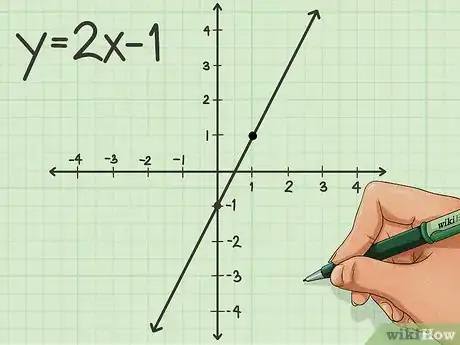
3Trova l'intercetta verticale (b) sul grafico. Se consideri un'equazione elementare come y=2x-1, puoi notare che "-1" si trova nella posizione in cui dovrebbe esserci "b"; questo significa che "-1" è l'intercetta.
- L'intercetta verticale viene sempre riportata nel sistema cartesiano con ascissa x=0; di conseguenza, le coordinate sono (0,-1).
- Disegna un punto sul piano cartesiano in corrispondenza dell'intercetta.
-
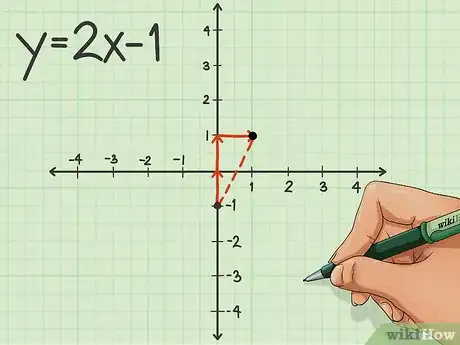
4Trova il coefficiente angolare. Nell'esempio considerato in precedenza, y=2x-1, la pendenza occupa la posizione corrispondente a "m" e puoi notare che è pari al numero "2"; tuttavia, la pendenza è il rapporto tra la quota e il percorso orizzontale, deve quindi essere espressa come una frazione. Poiché "2" è un numero intero, l'equivalente in frazione è "2/1".
- Per riportare il coefficiente angolare sul grafico, inizia dall'intercetta verticale. La quota (il numero di unità per le quali devi muoverti verso l'alto) corrisponde al numeratore della frazione, mentre il percorso orizzontale è dato dal denominatore.
- Per quanto riguarda l'esempio precedente, dovresti trovare la pendenza partendo dall'intercetta -1 e spostandoti di 2 unità verso l'alto e di 1 unità verso destra.
- Una quota positiva significa che devi spostarti verso l'alto lungo l'asse delle y, mentre un valore negativo corrisponde a un movimento verso il basso. Uno spostamento orizzontale positivo è sempre verso destra, uno negativo è sempre verso sinistra lungo l'asse delle x.
- Puoi tracciare tutte le coordinate che desideri usando il coefficiente angolare, ma devi definirne almeno una.
-
5Disegna la retta. Una volta definito almeno un altro punto sul piano cartesiano grazie alla pendenza, non ti resta che unirlo all'intercetta verticale con una retta. Prosegui la linea in entrambe le direzioni e aggiungi delle frecce alle sue estremità per indicare che continua all'infinito.Pubblicità
Disequazioni con una Incognita
-
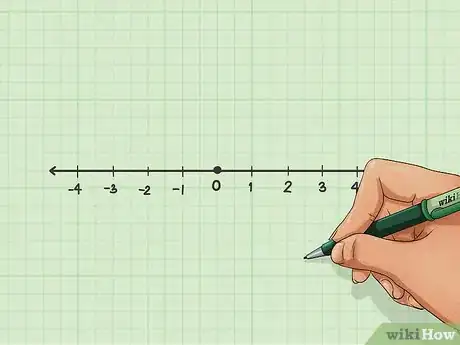
1Traccia una linea dei numeri. Dato che le disequazioni con una incognita si rappresentano con un solo asse, non è necessario disegnare un sistema di riferimento cartesiano; in tal caso, è sufficiente una linea dei numeri.
-
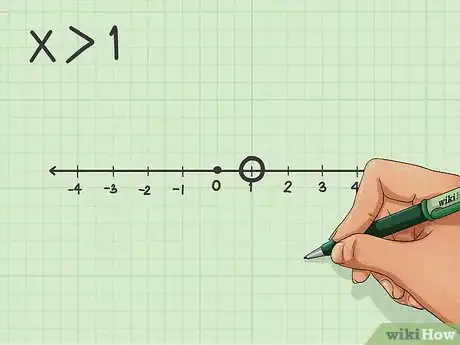
2Disegna il grafico. È una procedura piuttosto semplice perché lavori con una sola coordinata. Ti viene assegnata una disequazione, ad esempio x<1 da rappresentare in un grafico. Per prima cosa, trova il valore "1" sulla linea dei numeri.
- Se il problema si esprime con i segni "maggiore di" (>) oppure "minore di" (<), devi disegnare un cerchio vuoto attorno al numero sulla linea.
- Se è presente il simbolo "maggiore o uguale a" (≥) o "minore o uguale a" (≤), devi riempire il cerchio.
-
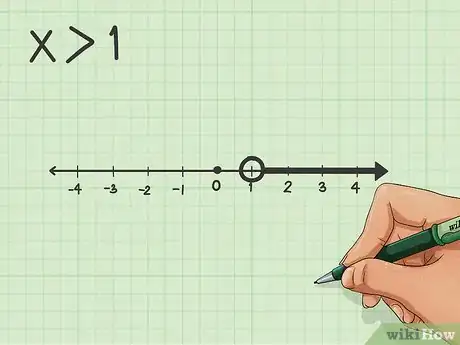
3Disegna la linea. Partendo dal punto che hai appena trovato, segui la direzione del simbolo della disequazione per rappresentarla graficamente. Se ti trovi di fronte al simbolo "maggiore di", la retta si estende verso destra e viceversa se il simbolo è quello "minore di". Aggiungi una freccia all'estremità della retta per indicare che prosegue e che non è un segmento.
-
4Verifica la tua risposta. Sostituisci l'incognita x con qualsiasi numero e riportalo graficamente sulla linea dei numeri; se questo si trova sulla semiretta che hai appena definito, il grafico è preciso.Pubblicità
Disequazioni Lineari
-
1Sfrutta la struttura dell'intercetta e del coefficiente angolare. Si tratta della medesima formula che hai utilizzato per disegnare il grafico delle equazioni lineari, ma in questo caso al posto del segno di uguaglianza (=) hai quello "maggiore di" (>) oppure "minore di" (<).
- La struttura dell'intercetta e della pendenza è y=mx+b, dove m=coefficiente angolare e b=intercetta verticale.
- Una disequazione prevede più di una soluzione.
-
2Traccia il grafico. Trova l'intercetta verticale e la pendenza per definirne le coordinate. Se utilizzi la disequazione elementare y>1/2x+1, l'intercetta è pari a "1". La pendenza è ½, il che significa che devi spostarti di una unità verso l'alto e due verso destra.
-
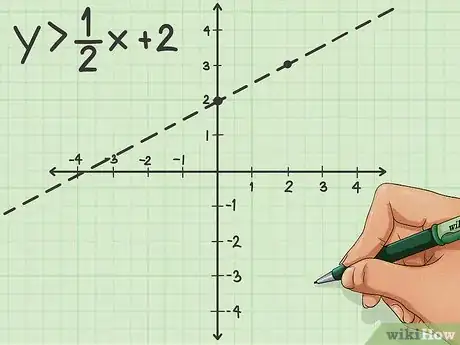
3Disegna la retta. Prima di continuare controlla però il simbolo presente nella diseguaglianza. Se si tratta di quello di maggioranza, la linea deve essere tratteggiata; se è quello di minoranza, deve essere una linea continua.
-
4Colora l'area. Poiché una disequazione prevede multiple soluzioni, devi mostrare tutte quelle possibili sul grafico colorando l'area che si trova sopra o sotto la linea.
- Scegli una coppia di coordinate; solitamente, l'origine (0,0) è il punto più semplice. Osserva se tale punto si trova sopra o sotto la linea che hai disegnato.
- Inserisci la coppia di coordinate nella disequazione al posto delle variabili. Considerando l'esempio precedente, ottieni: 0>1/2(0)+1; risolvi quindi la disequazione.
- Se il punto definito dalla coppia di coordinate si trova sopra la linea e la disequazione è vera, devi colorare l'area che si trova sopra la linea stessa; se la disequazione è falsa, devi colorare la porzione inferiore. Se il punto si trova sotto la linea e la disequazione è vera, colora la parte inferiore; se è falsa, devi aggiungere il colore alla zona soprastante.
- Ritornando all'esempio, il punto origine con coordinate (0,0) è sotto la linea tracciata e rende falsa la disequazione quando sostituisci le incognite; questo significa che devi colorare la porzione di grafico sopra la retta.[1]
Pubblicità
Equazioni di Secondo Grado
-
1Studia il problema. Un'equazione di secondo grado contiene almeno una incognita elevata alla seconda potenza; solitamente, viene scritta nella forma y=ax2+bx+c.
- Il grafico di una equazione di questo tipo è una parabola, una curva a forma di "U".
- Devi trovare almeno tre punti per disegnare tale grafico, iniziando dal vertice cioè il punto centrale.
-
2Trova i coefficienti "a", "b" e "c". Se consideri l'esempio y=x2+2x+1, a=1, b=2 e c=1. Ciascuna lettera corrisponde al numero che si trova direttamente prima della variabile a cui si accompagna nell'equazione; se non c'è alcun numero prima della x, il coefficiente è pari 1.
-
3Trova il vertice. Si tratta del punto centrale della parabola e puoi individuarlo utilizzando la formula -b/2a. Nell'equazione precedente, questo significa -2/2(1), cioè -1.
-
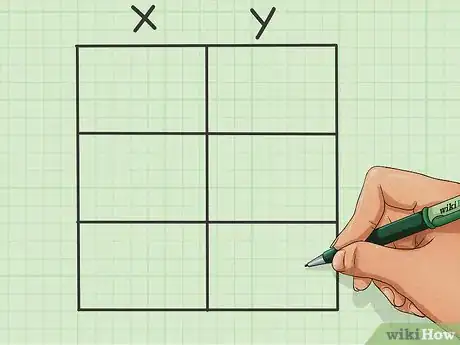
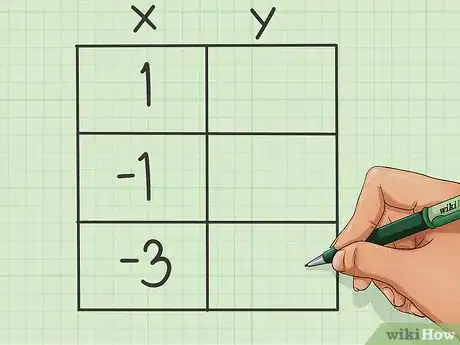
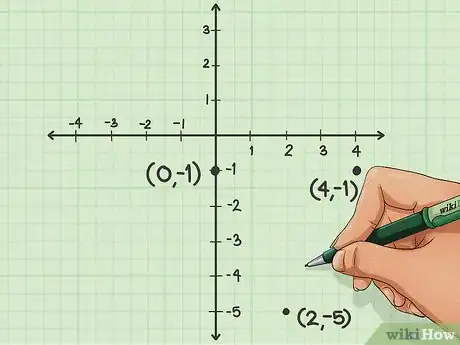
4Costruisci una tabella. Sai che il vertice ha ascissa -1; tuttavia, si tratta solamente di uno dei due valori che costituiscono una coppia di coordinate. Per trovare l'ordinata e gli altri due punti della parabola, devi realizzare una tabella.
-
5Disegnane una con tre righe e due colonne.
- Scrivi la coordinata x del vertice nella parte superiore della colonna centrale.
- Scegli altre due ascisse simmetriche rispetto a quella del vertice; per esempio, puoi aumentare e diminuire il valore di due unità e trovare i valori "-3" e "1".
- Puoi scegliere qualsiasi coppia di numeri per completare la prima riga della tabella, purché siano simmetrici e interi.
- Se vuoi ottenere un grafico più definito, puoi trovare cinque coppie di coordinate invece di tre; rispetta il medesimo processo, ma disegna cinque colonne anziché tre.
-
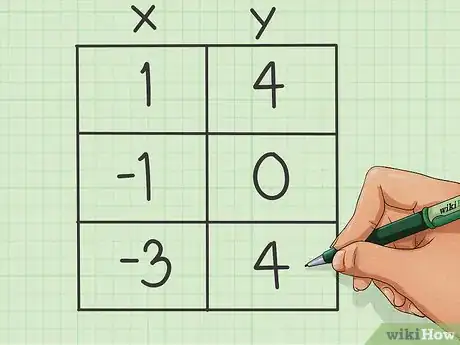
6Sfrutta la tabella e l'equazione per trovare i valori corrispondenti di y. Prendi uno alla volta i numeri che hai scelto e che rappresentano le ascisse e sostituiscili a "x" nell'equazione; risolvi la formula per "y".
- Considerando l'esempio utilizzato finora, puoi usare la coordinata "-3" e inserirla nella formula originale y=x2+2x+1, trasformandola in y= -32+2(3)+1, cioè y=4.
- Riporta l'ordinata appena trovata sotto l'ascissa corrispondente all'interno della tabella.
- Prosegui nello stesso modo per tutte e tre (o cinque) le ascisse.
-
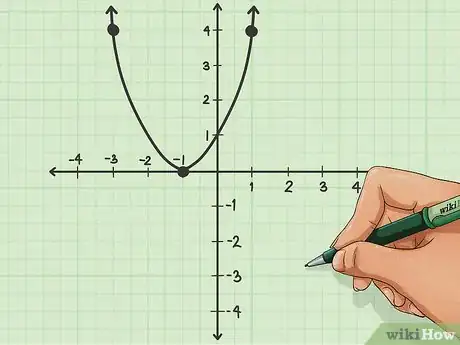
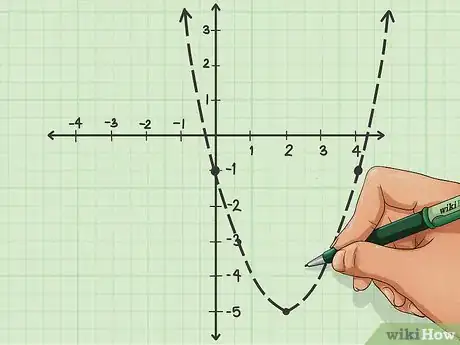
7Riporta i punti sul grafico. Ora che hai almeno tre coppie complete di coordinate, puoi disegnarle sul piano cartesiano; connettile con una linea parabolica e hai finito!Pubblicità
Disequazioni di Secondo Grado
-
1Risolvi la disequazione di secondo grado. La forma è la stessa di un'equazione di secondo grado, ma il simbolo di uguaglianza è sostituito da quello di disuguaglianza; ad esempio, il problema può presentarsi come y<ax2+bx+c. Sfruttando i passaggi descritti nella sezione precedente, trova i tre punti della parabola.
-
2Riporta le coordinate sul sistema cartesiano. Sebbene tu abbia i tre punti necessari per disegnare la parabola, per il momento non tracciarla.
-
3Unisci i tre punti sul grafico. Dato che stai rappresentando una disequazione di secondo grado, la linea deve essere leggermente diversa.
- Se il simbolo usato è "maggiore di" o "minore di" (> o <), devi utilizzare una linea tratteggiata.
- Se il simbolo è "maggiore o uguale a" oppure "minore o uguale a" (≥ o ≤), usa una linea continua.
- Aggiungi una freccia a entrambe le estremità per indicare che la linea si estende oltre i limiti del grafico.
-
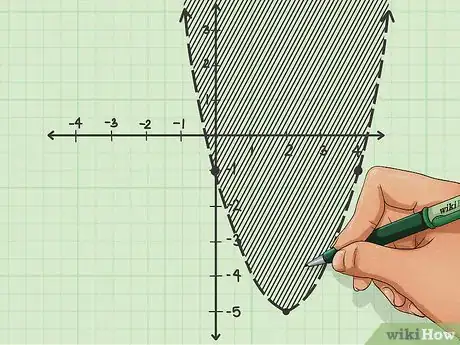
4Colora il grafico. Per rappresentare le soluzioni multiple di una disequazione devi colorare l'area in cui potrebbero essere contenute; per procedere devi inserire una coppia di coordinate nella disequazione e risolverla. L'origine (0,0) è il punto più semplice da usare; osserva se questo si trova all'interno o all'esterno della concavità della parabola.
- Risolvi la disequazione con le coordinate che hai scelto. Se usi l'esempio precedente, y>x2-4x-1, e sostituisci le incognite con le coordinate (0,0), ottieni: 0>02-4(0)-1.
- Se la soluzione rende vera la disuguaglianza e il punto si trova dentro la concavità, colora la porzione interna; se invece è falsa, colora la parte esterna.
- Se la soluzione è vera e il punto è esterno alla figura, colora la parte esterna, altrimenti quella interna.[2]
Pubblicità
Equazioni con Valore Assoluto
-
1Esamina l'equazione. La versione più semplice di un'equazione con valore assoluto è y=|x|; tuttavia, potrebbero essere coinvolte altre variabili o altri numeri.
-
2Imponi che il valore assoluto sia nullo. Per farlo scrivi tutto quello che si trova tra le due linee verticali (| |) pari a 0. Se consideri l'esempio y=|x-2|+1, devi scrivere |x-2|=0; di conseguenza, il valore assoluto diventa 2.
- Il valore assolto corrisponde al numero |x| di unità dal punto "0" sulla linea dei numeri, ne consegue che il valore di |2| è 2 e quello di |-2| è sempre 2; questo perché in entrambi i casi i numeri si trovano a due unità dallo zero.
- Potresti avere un'equazione con valore assoluto pari alla sola incognita "x"; in tal caso, il valore assoluto è "0". Per esempio, y=|x|+3 diventa y=|0|+3, cioè "3".
-
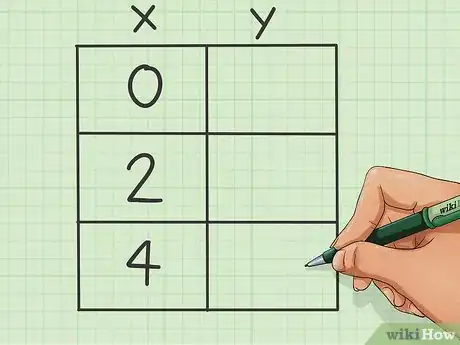
3Realizza una tabella. Ti servono due colonne e tre righe.
- Inserisci la coordinata del primo valore assoluto nella prima riga della colonna per "x".
- Scegli altre due ascisse simmetriche rispetto al primo valore; se |x|=0, devi aumentare e diminuire il numero della stessa quantità di unità.
- Puoi scegliere qualsiasi numero, anche se quelli prossimi alla prima ascissa che hai trovato sono i più utili; ricorda che devono essere anche interi.
-
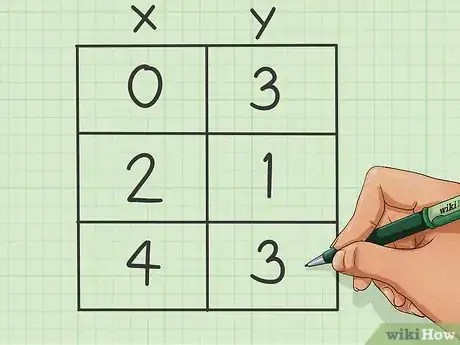
4Risolvi l'equazione. Devi trovare le ordinate che corrispondono alle ascisse appena definite. Per farlo sostituisci l'incognita "x" con il numero scelto e risolvi l'equazione per "y"; annota le soluzioni nella tabella.
-
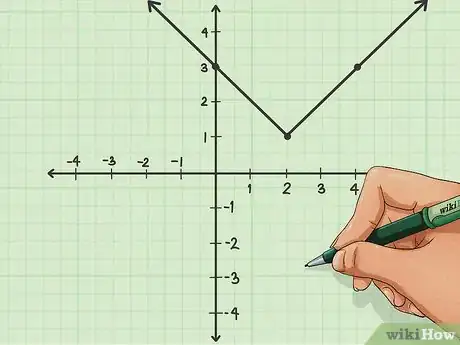
5Riporta i punti sul grafico. Te ne servono solamente tre per tracciare il grafico di un'equazione con valore assoluto, ma puoi usarne quanti ne vuoi. La rappresentazione grafica di un'equazione di questo tipo ha sempre una forma a "V". Aggiungi delle frecce alle estremità per indicare che le linee si estendono oltre i limiti del disegno.[3]Pubblicità
Consigli
- Per tracciare i grafici delle equazioni è meglio usare la carta millimetrata.
- Chiedi a un amico o all'insegnante di controllare il tuo lavoro per verificare che sia stato svolto correttamente.
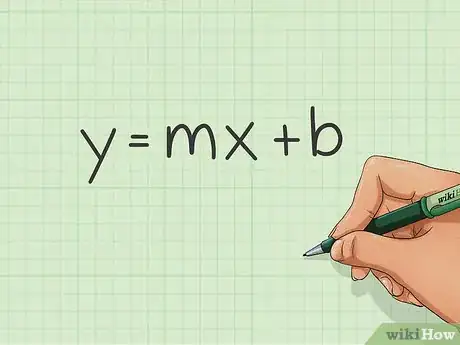
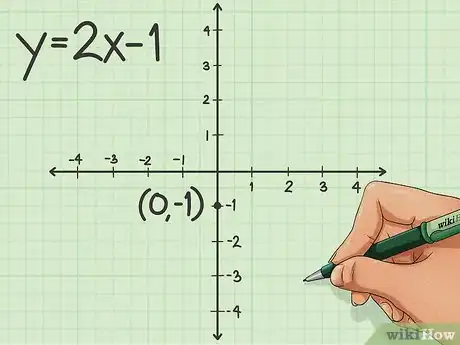
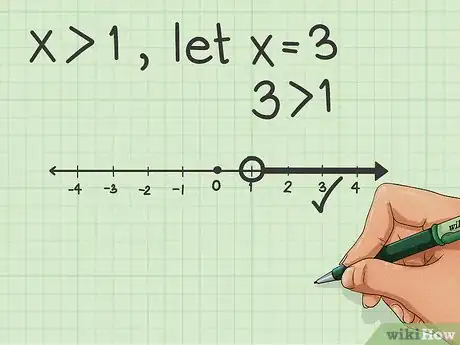
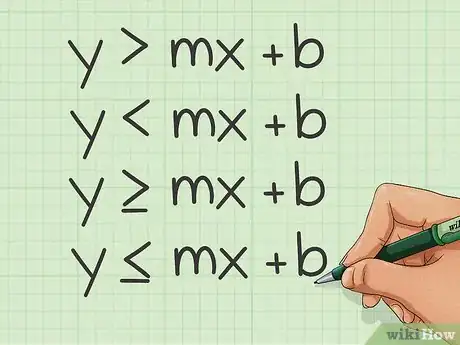
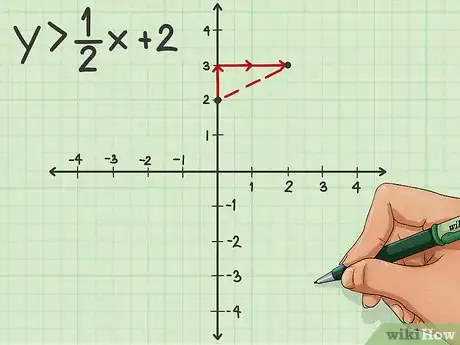

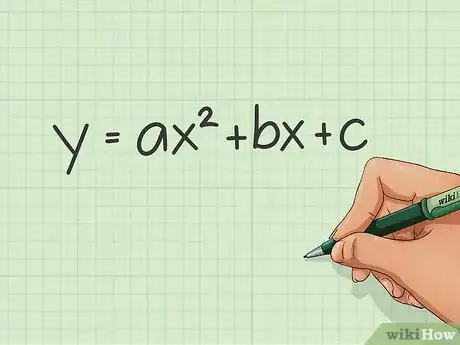
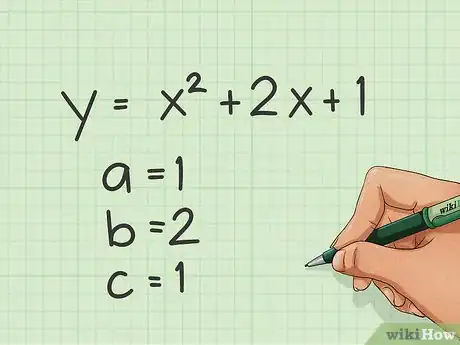
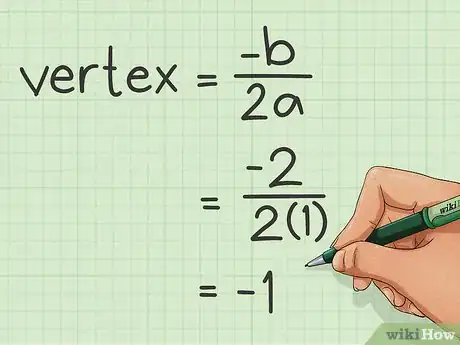
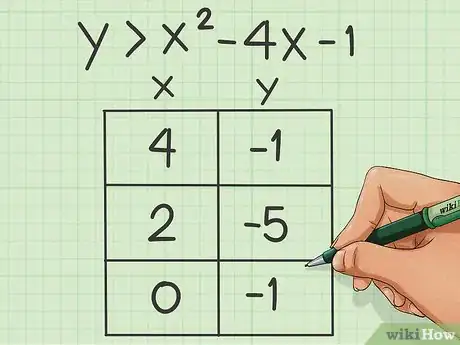
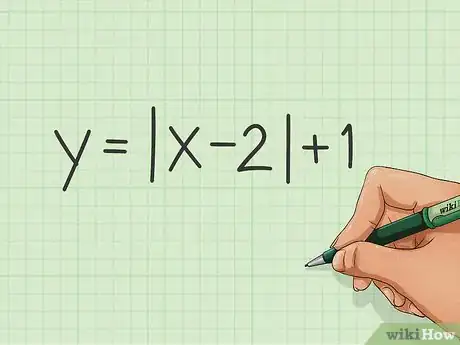
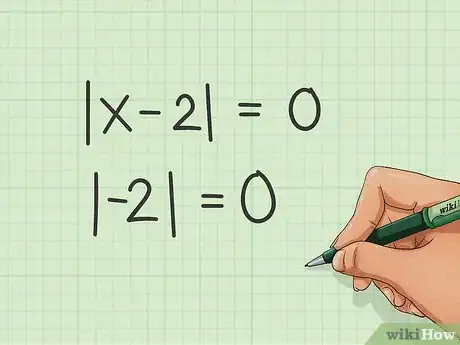



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
