wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 18 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 29 574 volte
Media, mediana e moda sono valori che si possono incontrare con frequenza nell'ambito statistico di base e nei calcoli matematici che si affrontare tutti i giorni.[1] Calcolare questi valori è molto semplice, ma lo è altrettanto confonderne il significato. Leggi questo articolo per scoprire come calcolare la media, la mediana e la moda di un insieme di dati.
Passaggi
Media
-
1Somma fra loro tutti i numeri dell'insieme di dati che stai studiando.[2] Ipotizza di dover analizzare i seguenti dati: 2, 3 e 4. La somma di tutti i valori indicati è pari a: 2 + 3 + 4 = 9.
-
2Conta il numero di valori che costruiscono il tuo insieme di dati. Proseguendo con l'esempio precedente stai lavorando con 3 numeri.
-
3Dividi la somma che hai calcolato nel primo passaggio per il numero di elementi dell'insieme. In questo caso dovrai dividere la somma, cioè 9, per il numero di valori dell'insieme che stai studiando, cioè 3, ottenendo: 9 / 3 = 3. La media del tuo insieme di valori è pari a 3. Ricorda che non sempre otterrai un valore intero come media di un insieme di dati.[3]Pubblicità
Mediana
-
1Ordina la serie di numeri che vuoi studiare in ordine crescente.[4] Ipotizza di dover lavorare con i seguenti valori: 4, 2, 8, 1 e 15. Ordinando la serie numerica dal valore più piccolo a quello più grande otterrai: 1, 2, 4, 8 e 15.
-
2Individua l'elemento centrale della serie numerica. Il modo in cui farlo varia in base al fatto di studiare un insieme di dati composto da un numero pari o dispari di elementi.[5] Ecco come dovrai comportarti in entrambi gli scenari possibili:
- Se l'insieme di dati è composto da un numero dispari di elementi, elimina il numero dell'insieme che si trova all'estrema sinistra, poi elimina il valore che si trova all'estrema destra e ripeti finché non rimane un solo valore. Quest'ultimo numero rappresenta la mediana dell'insieme di dati che stai analizzando. Facendo riferimento all'insieme di numeri 4, 7, 8, 11 e 21 si intuisce che la mediana è il numero 8, dato che rappresenta l'elemento centrale della serie.
- Se l'insieme di dati è composto da un numero pari di elementi, elimina un numero alla volta da ciascuna estremità della serie finché non ne rimangono solo due. A questo punto calcola la media dei valori che sono rimasti. Nel caso speciale in cui i due valori rimasti sono uguali significa che la mediana è esattamente tale numero.[6] Se stai lavorando sulla serie di numeri 1, 2, 3, 5, 7 e 10, dovrai calcolare la media dei valori 5 e 3. Sommando i numeri in oggetto otterrai 5 + 3 = 8. Dividendo la somma per il numero di elementi otterrai che la mediana è pari a 8 / 2 = 4.
Pubblicità
Moda
-
1Prendi nota di tutti i valori dell'insieme che vuoi studiare. Ipotizza di dover analizzare la seguente serie di numeri: 2, 4, 5, 5, 4 e 5. Anche in questo caso ti sarà di aiuto ordinare l'insieme di dati da elaborare in ordine crescente.
-
2Individua il numero che si presenta con maggiore frequenza all'interno della serie di valori in oggetto. La moda di una serie di numeri è l'elemento che ha più occorrenze all'interno dell'insieme.[7] Analizzando il problema di esempio si intuisce che la moda sia il numero 5, dato che si presenta per ben 3 volte. Se all'interno di un insieme di dati sono presenti due elementi con la medesima frequenza, allora si parla di una distribuzione "bimodale". Nel caso di un insieme di dati in cui ci sono più di due valori con la medesima frequenza si usa il termine "multimodale".Pubblicità
Consigli
- Per individuare più facilmente la mediana e la moda, ordina in modo crescente la serie di numeri su cui devi lavorare.
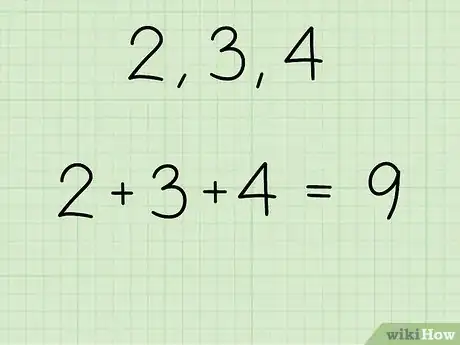

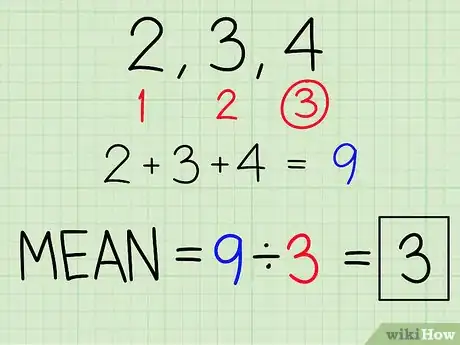







-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
