wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 39 785 volte
Nel calcolo differenziale, un punto di flesso è un punto su una curva in cui la curvatura cambia di segno (da positivo a negativo o viceversa). E' utilizzato in varie materie, inclusa l'ingegneria, l'economia, e la statistica, per determinare cambiamenti fondamentali all'interno dei dati. Se hai bisogno di trovare un punto di flesso in una curva, vai allo Step 1.
Passaggi
Capire i Punti di Flesso
-
1Capire le funzioni concave. Per capire i punti di flesso, hai bisogno di distinguere funzioni concave da quelle convesse. Una funzione concava è una funzione in cui presa una qualsiasi linea che congiunge due punti del suo grafico, non sta mai sopra il grafico.
-
2Capire le funzioni convesse. Una funzione convessa è essenzialmente l'opposto di una funzione concava: è una funzione in cui qualsiasi linea che congiunge due punti del suo grafico, non sta mai sotto il grafico.
-
3Capire la radice di una funzione. Una radice di una funzione è il punto in cui la funzione è uguale a zero.
- Se si dovesse rappresentare graficamente una funzione, le radici sarebbero i punti in cui la funzione interseca l'asse x.
Pubblicità
Trovare le Derivate di una Funzione
-
1Trovare la derivata prima della funzione. Prima che tu possa trovare i punti di flesso, dovrai trovare le derivate della tua funzione. La derivata di una funzione di base può essere trovata in qualsiasi testo di analisi; devi impararle prima che tu possa passare a dei compiti più complessi. Le derivate prime sono indicate con f ′(x). Per espressioni polinomiali della forma axp + bx(p−1) + cx + d, la derivata prima è apx(p−1) + b(p − 1)x(p−2) + c.
- Per esempio, supponiamo che tu debba trovare il punto di flesso della funzione f(x) = x3 +2x−1. Calcola la derivata prima della funzione nel seguente modo:
f ′(x) = (x3 + 2x − 1)′ = (x3)′ + (2x)′ − (1)′ = 3x2 + 2 + 0 = 3x2 + 2
- Per esempio, supponiamo che tu debba trovare il punto di flesso della funzione f(x) = x3 +2x−1. Calcola la derivata prima della funzione nel seguente modo:
-
2Trovare la derivata seconda della funzione. La derivata seconda è la derivata della derivata prima della funzione, indicata con f ′′(x).
- Nell'esempio sopra, la derivata seconda avrà il seguente aspetto:
f ′′(x) = (3x2 + 2)′ = 2 × 3 × x + 0 = 6x
- Nell'esempio sopra, la derivata seconda avrà il seguente aspetto:
-
3Uguagliare la derivata seconda a zero. Uguaglia a zero la tua derivata seconda e trova le soluzioni. La tua risposta sarà un possibile punto di flesso.
- Nell'esempio sopra, il tuo calcolo avrà il seguente aspetto:
f ′′(x) = 0
6x = 0
x=0
- Nell'esempio sopra, il tuo calcolo avrà il seguente aspetto:
-
4Trovare la derivata terza della funzione. Per capire se la tua soluzione è effettivamente un punto di flesso, trova la derivata terza, che è la derivata della derivata seconda della funzione, indicata con f ′′′(x).
- Nell'esempio sopra, il tuo calcolo avrà il seguente aspetto:
f ′′′(x) = (6x)′ = 6
Pubblicità - Nell'esempio sopra, il tuo calcolo avrà il seguente aspetto:
Trovare il punto di flesso
-
1Valutare la derivata terza. La regola standard per calcolare un possibile punto di flesso come segue: "Se la derivata terza non è uguale a 0, allora f ′′′(x) ≠ 0, il possibile punto di flesso è effettivamente un punto di flesso." Controlla la tua derivata terza. Se non è uguale a 0 nel punto, è un flesso reale.
- Nell'esempio sopra, la tua derivata terza calcolata è 6, non 0. Perciò, è un punto di flesso reale.
-
2Trovare il punto di flesso. La coordinata del punto di flesso è indicata come (x,f(x)), dove x è il valore della variabile x nel punto di flesso e f(x) è il valore della funzione nel punto di flesso.
- Nell'esempio sopra, ricorda che quando calcoli la derivata seconda, trovi che x = 0. Quindi, devi trovare f(0) per determinare le coordinate. Il tuo calcolo avrà il seguente aspetto:
f(0) = 03 +2×0−1 = −1.
- Nell'esempio sopra, ricorda che quando calcoli la derivata seconda, trovi che x = 0. Quindi, devi trovare f(0) per determinare le coordinate. Il tuo calcolo avrà il seguente aspetto:
-
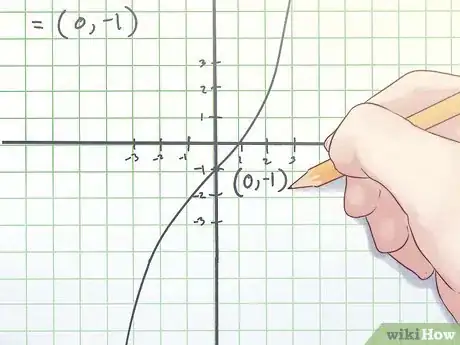
3Annotare le coordinate. Le coordinate del tuo punto di flesso sono il valore della x e il valore calcolato sopra.
- Nell'esempio precedente le coordinate del punto di flesso sono (0, -1).
Pubblicità
Consigli
- La derivata prima di una costante è sempre 0.
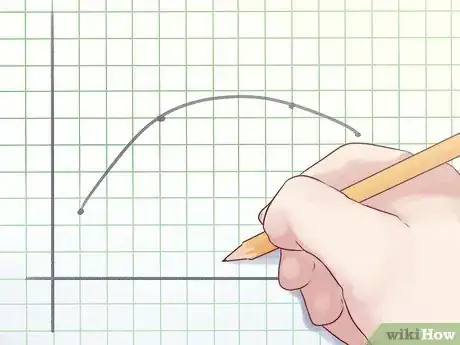
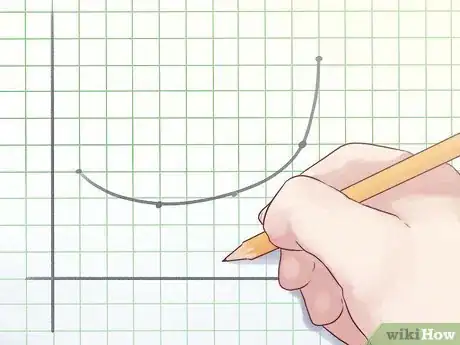

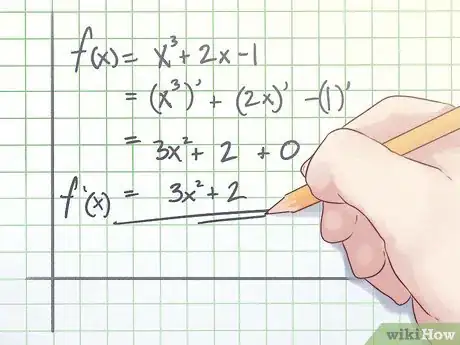

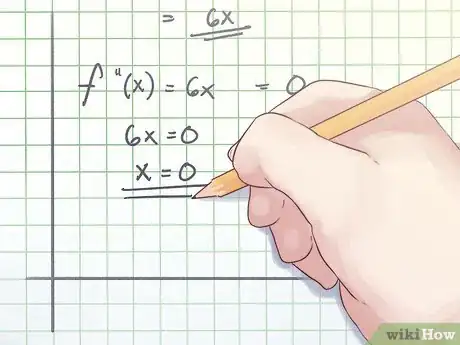
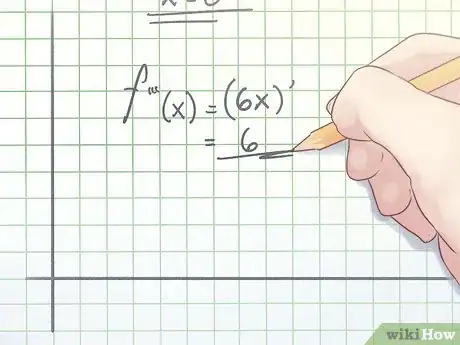

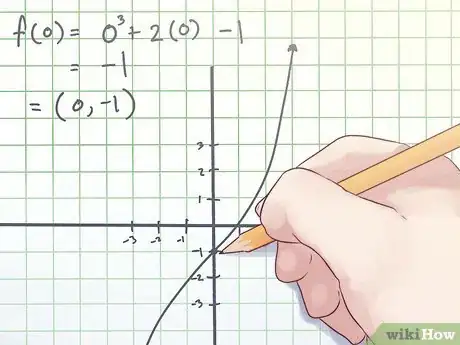



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
