Questo articolo è stato co-redatto da David Jia. David Jia è un tutor accademico e fondatore di LA Math Tutoring, una società privata di tutoraggio con sede a Los Angeles. Con oltre 10 anni di esperienza nell'insegnamento, David lavora con studenti di tutte le età e di tutti i livelli in varie materie. Offre inoltre consulenze per ammissioni ai college statunitensi e preparazione ai test SAT, ACT, ISEE e altri. Dopo avere ottenuto un punteggio perfetto al test SAT (800 in matematica e 690 in inglese), ha vinto la borsa di studio Dickinson alla University of Miami, dove si è laureato in Business Administration. Ha inoltre partecipato a video educativi online per case editrici come Larson Texts, Big Ideas Learning e Big Ideas Math.
Questo articolo è stato visualizzato 23 286 volte
Il codominio o rango di una funzione è l'insieme dei valori che la funzione può assumere. In altre parole, è l'insieme dei valori y che si ottengono quando si inseriscono tutti i possibili valori di x nella funzione. Questo insieme di possibili valori di x è chiamato il dominio. Se vuoi sapere come trovare il rango di una funzione, basta seguire questi passaggi.
Passaggi
Trovare il Rango di una Funzione Avendo una Formula
-
1Scrivi la formula. Supponiamo che sia la seguente: f (x) = 3 x2+ 6 x - 2. Questo significa che, inserendo una qualsiasi x nell'equazione, si otterrà il corrispettivo valore y. Questa è la funzione di una parabola.[1]
-
2Trova il vertice della funzione se è quadratica. Se stai lavorando con una linea retta o con un polinomio di un grado dispari, ad esempio f (x) = 6 x3 + 2 x + 7, puoi saltare questo passaggio. Ma, se stai lavorando con una parabola o qualsiasi equazione dove la coordinata x è al quadrato o elevata a una potenza pari, è necessario tracciare il vertice. Per farlo, basta usare la formula -b/2a per ottenere la coordinata x del vertice della funzione 3 x2 + 6 x - 2, dove 3 = a, 6 = b e - 2 = c. In questo caso - b è -6 e 2 a è 6, quindi la coordinata x è -6/6 o -1.
- Ora inserisci -1 nella funzione per ottenere la coordinata y. f(-1) = 3(-1)2 + 6(-1) - 2 = 3 - 6 - 2 = - 5.
- Il vertice è (-1, - 5). Fai il grafico disegnando un punto dove la coordinata x è -1 e y è - 5. Dovrebbe essere nel terzo quadrante del grafico.
-
3Trova alcuni altri punti nella funzione. Per farti un'idea della funzione, dovresti sostituire altre coordinate x in modo da avere un’idea di come appare la funzione, prima ancora di iniziare a cercare il codominio. Poiché è una parabola e il coefficiente davanti alla x2 è positivo (+3), essa sarà rivolta verso l'alto. Ma, solo per darti un’idea, inseriamo alcune coordinate x nella funzione per vedere quali valori y restituisce:[2]
- f(- 2) = 3(- 2)2 + 6(- 2) - 2 = -2. Un punto sul grafico è (-2; -2)
- f(0) = 3(0)2 + 6(0) - 2 = -2. Un altro punto sul grafico è (0; -2)
- f(1) = 3(1)2 + 6(1) - 2 = 7. Un terzo punto sul grafico è (1; 7)
-
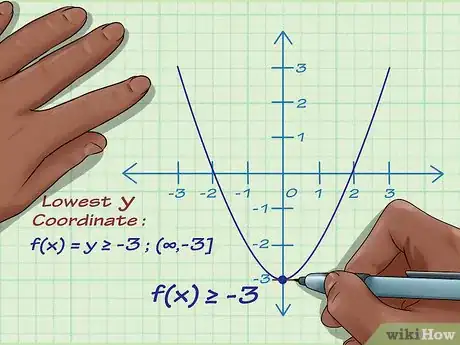
4Trova il codominio sul grafico. Ora osserva le coordinate y sul grafico e trova il punto più basso in cui il grafico tocca una coordinata y. In questo caso, la coordinata y più bassa è nel vertice, -5, e il grafico si estende all’infinito sopra questo punto. Questo significa che il codominio della funzione è y = tutti i numeri reali ≥ -5.[3]Pubblicità
Trovare il Codominio sul Grafico di una Funzione
-
1Trova il minimo della funzione. Cerca la coordinata y minima della funzione. Supponiamo che la funzione raggiunga il suo punto più basso a -3. y = -3 potrebbe anche essere un asintoto orizzontale: la funzione si potrebbe avvicinare a -3 senza mai toccarlo.
-
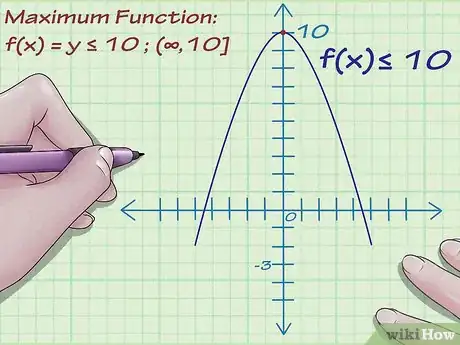
2Trova il massimo della funzione. Supponiamo che la funzione raggiunga il suo punto più alto a 10. y = 10 potrebbe anche essere un asintoto orizzontale: la funzione si potrebbe avvicinare a 10 senza mai toccarlo.
-
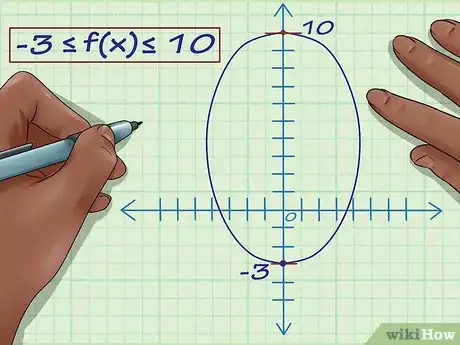
3Individua il rango. Questo significa che il codominio della funzione – l'intervallo di tutte le possibili coordinate y – varia da -3 a 10. Così, -3 ≤ f (x) ≤ 10. Ecco il rango della funzione.
- Supponiamo che il grafico raggiunga il suo punto più basso a y = -3, ma vada sempre verso l'alto. Allora il rango è f (x) ≥ -3.
- Supponiamo che il grafico raggiunga il suo punto più alto a 10, ma che vada sempre verso il basso. Allora il rango è f (x) ≤ 10.
Pubblicità
Trovare il Rango di una Relazione
-
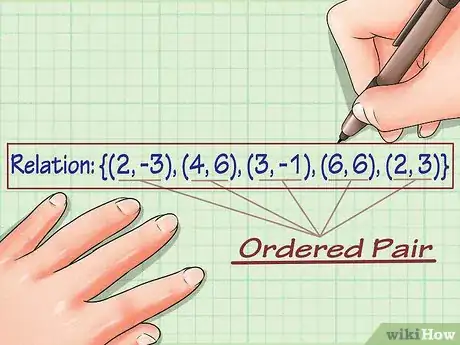
1Scrivi la relazione. Una relazione è un insieme di coppie ordinate di coordinate x e y. Si può guardare una relazione e determinare i suoi dominio e codominio. Supponi di avere la seguente relazione: {(2, -3), (4, 6), (3, -1), (6, 6), (2, 3)}.[4]
-
2Elenca le coordinate y della relazione. Per trovare il rango, semplicemente devi annotare tutte le coordinate y di ogni coppia ordinata: {-3, 6, -1, 6, 3}.[5]
-
3Rimuovi le coordinate duplicate in modo da averne solo una di ogni coordinata y. Noterai che hai elencato "6" due volte. Toglilo, in modo da rimanere con {-3, -1, 6, 3}.[6]
-
4Scrivi il rango della relazione in ordine crescente. Adesso riordina i numeri nell’insieme dal più piccolo al più grande, e avrai il rango della relazione {(2; -3), (4; 6), (3; -1), (6; 6), (2; 3)}: {-3; -1; 3; 6}. È tutto.[7]
-
5Assicurati che la relazione sia una funzione. Perché una relazione sia una funzione, ogni volta che si ha una certa coordinata x si deve avere la stessa coordinata y. Ad esempio, la relazione {(2, 3) (2, 4) (6, 9)} non è una funzione, perché quando si mette 2 come x, la prima volta si ottiene 3, mentre la seconda volta si ha 4. Perché una relazione sia una funzione, se inserisci lo stesso input, dovresti sempre ottenere lo stesso risultato in output. Se, ad esempio, inserisci -7, dovresti ottenere ogni volta la stessa coordinata y, qualunque essa sia.[8]Pubblicità
Trovare il Rango di una Funzione Descritta a Parole da un Problema
-
1Leggi il problema. Supponi di stare lavorando con il seguente problema: Barbara sta vendendo i biglietti per la recita della sua scuola a 5 euro ciascuno. La quantità di denaro che lei raccoglie è una funzione di quanti biglietti vende. Qual è il codominio della funzione?
-
2Scrivi il problema sotto forma di funzione. In questo caso, M rappresenta la quantità di denaro che Barbara raccoglie e t la quantità di biglietti che vende. Poiché ogni biglietto ha un costo di 5 euro, sarà necessario moltiplicare la quantità di biglietti venduti per 5 per trovare la quantità di denaro. Pertanto la funzione può essere scritta come M(t) = 5 t.
- Ad esempio, se Barbara vende 2 biglietti, devi moltiplicare 2 per 5 per ottenere 10, la quantità di euro ottenuti.
-
3Determina il dominio. Per determinare il rango, devi prima trovare il dominio. Il dominio è costituito da tutti i possibili valori di t che possono essere inseriti nell'equazione. In questo caso, Barbara può vendere 0 biglietti o più – non può vendere biglietti negativi. Poiché non sappiamo il numero di posti nell’auditorium della sua scuola, possiamo supporre che lei possa vendere teoricamente un numero infinito di biglietti. E può solo vendere biglietti interi: non può vendere mezzo biglietto, ad esempio. Pertanto il dominio della funzione è t = qualsiasi numero intero non negativo.
-
4Determina il rango. Il codominio è la quantità possibile di denaro che Barbara può ottenere con la sua vendita. Devi lavorare con il dominio per trovare il rango. Se sai che il dominio è qualsiasi numero intero non negativo e che la formula è M(t) = 5t, allora sai che è possibile inserire qualsiasi numero intero non negativo in questa funzione per ottenere l'insieme degli output o rango. Ad esempio, se vende 5 biglietti, allora M(5) = 5 x 5 = 25 euro. Se ne vende 100, allora M(100) = 5 x 100 = 500 euro. Di conseguenza il rango della funzione è qualsiasi intero non negativo che sia un multiplo di 5.
- Ciò significa che qualsiasi numero intero non negativo che è un multiplo di cinque è un possibile output per l'input della funzione.
Pubblicità
Consigli
- Vedi se riesci a trovare l'inversa della funzione. Il dominio dell’inversa di una funzione è uguale al rango di tale funzione.
- Controlla per vedere se la funzione si ripete. Qualsiasi funzione che si ripete lungo l'asse x avrà lo stesso rango per l'intera funzione. Per esempio, f (x) = sen(x) ha un rango compreso tra -1 e 1.
Riferimenti
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:functions/x2f8bb11595b61c86:introduction-to-the-domain-and-range-of-a-function/v/domain-of-a-function-intro
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:functions/x2f8bb11595b61c86:introduction-to-the-domain-and-range-of-a-function/v/domain-of-a-function-intro
- ↑ https://www.khanacademy.org/math/algebra/x2f8bb11595b61c86:functions/x2f8bb11595b61c86:introduction-to-the-domain-and-range-of-a-function/v/domain-of-a-function-intro
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.purplemath.com/modules/fcns2.htm
- ↑ http://www.mathsisfun.com/sets/domain-range-codomain.html
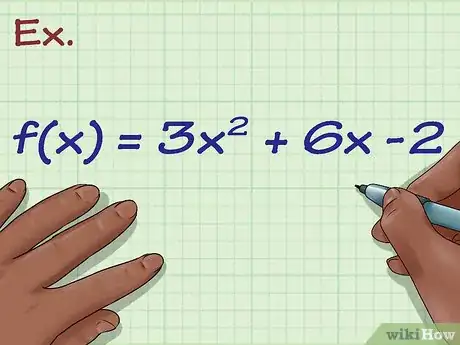





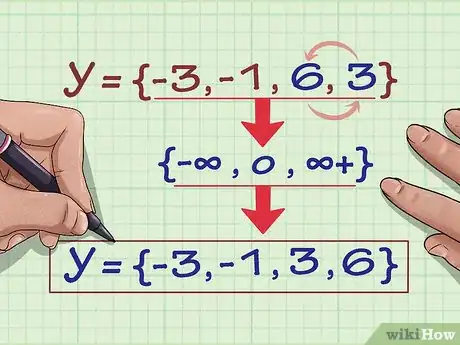









-to-Grams-(g)-Step-12-Version-4.webp)














