Questo articolo è stato co-redatto da Jake Adams. Jake Adams è un tutor accademico e titolare di PCH Tutors, un'attività con sede a Malibù, in California, che offre tutoraggio e risorse di apprendimento per aree disciplinari che vanno dalla scuola materna all'università, preparazione SAT e ACT (test per l'ammissione ai college statunitensi) e consulenze in materia di ammissione ai college. Con oltre 11 anni di esperienza nel settore, Jake è anche il CEO di Simplifi EDU, un servizio di tutoraggio online il cui scopo è quello di fornire ai clienti accesso a una rete di eccellenti tutor californiani. Jake ha conseguito una laurea in Business Internazionale e Marketing presso la Pepperdine University.
Questo articolo è stato visualizzato 60 013 volte
In ambito matematico sapere come individuare o calcolare il numero di diagonali di un poligono è una delle capacità basilari che occorre acquisire. A prima vista può sembrare un compito difficile da svolgere, ma in realtà è molto più semplice di quello che sembra una volta imparato il metodo. Per diagonale di un poligono si definiscono tutti i segmenti che congiungono due vertici non consecutivi della figura geometrica.[1] Si definisce poligono una qualsiasi figura geometrica che abbia più di tre lati. Utilizzando una semplice formula matematica è possibile calcolare il numero di diagonali di un qualsiasi poligono, indipendentemente dal fatto che abbia 4 o 4.000 lati.
Passaggi
Disegnare le Diagonali
-
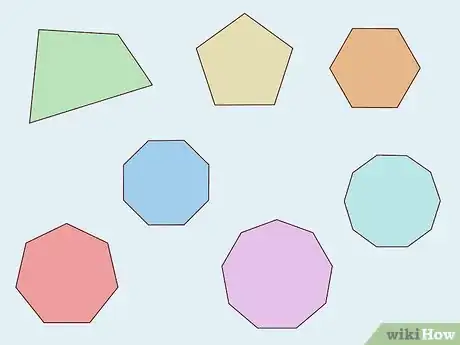
1Impara i nomi dei poligoni. La prima cosa da fare è individuare il numero di lati che compongono il poligono in esame. Il nome di ogni poligono è composto da un prefisso che ne identifica il numero di lati. Di seguito sono elencati i nomi dei poligoni composti da 4 fino a 20 lati:[2]
- Tetragono/Quadrilatero: 4 lati;
- Pentagono: 5 lati;
- Esagono: 6 lati;
- Ettagono: 7 lati;
- Ottagono: 8 lati;
- Ennagono: 9 lati;
- Decagono: 10 lati;
- Endecagono: 11 lati;
- Dodecagono: 12 lati;
- Tridecagono: 13 lati;
- Tetradecagono: 14 lati;
- Pentadecagono: 15 lati;
- Esadecagono: 16 lati;
- Ettadecagono: 17 lati;
- Ottadecagono: 18 lati;
- Ennadecagono: 19 lati;
- Icosagono: 20 lati;
- Nota che il triangolo, pur essendo un poligono, non presenta diagonali.[3]
-
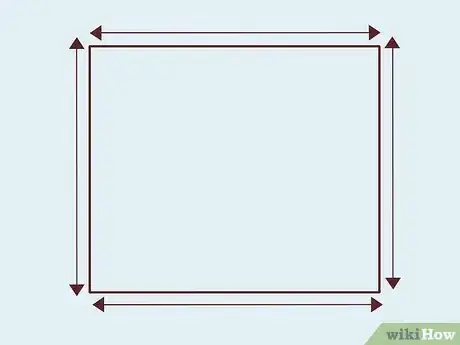
2Disegna il poligono che vuoi studiare. Se vuoi conoscere il numero di diagonali presenti in un quadrato, inizia disegnando la figura geometrica in oggetto. Il modo più semplice per individuare il numero di diagonali di un poligono simmetrico (in cui ogni lato ha la medesima lunghezza) consiste nel disegnarle e contarle. È importante precisare che, anche nel caso di un poligono non simmetrico, il numero di diagonali sarà comunque il medesimo.[4]
- Per disegnare un poligono simmetrico, utilizza un righello in modo da poter tracciare i lati della medesima lunghezza e poterli congiungere fra loro in modo preciso.
- Se non sai quale sia l'aspetto del poligono che devi disegnare, cerca un'immagine nel web. Per esempio il nome del poligono che ha inspirato il cartello stradale di stop è l'ottagono.
-
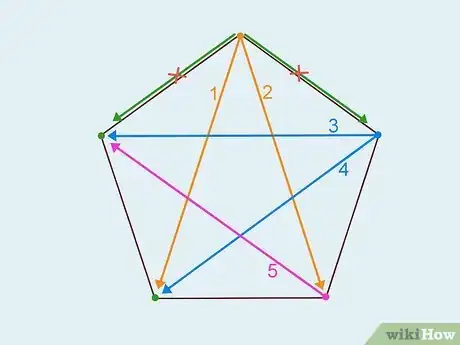
3Disegna le diagonali. Per diagonale di un poligono si intende il segmento che congiunge due vertici della figura non consecutivi (in questo caso si escludono i lati perché questi ultimi congiungono invece due vertici del poligono consecutivi).[5] Parti da un vertice del poligono e utilizza un righello per tracciare una linea retta che lo congiunge a tutti gli altri angoli disponibili.
- Nel caso di un quadrato disegna una linea che congiunga l'angolo inferiore sinistro della figura con quello superiore destro e una seconda linea che congiunga l'angolo inferiore destro con quello superiore sinistro.
- Disegna ogni diagonale utilizzando un colore differente, in modo da poterle contare con più facilità.[6]
- Nota che l'applicazione di questo metodo risulta essere molto più difficile quando si studiano i poligoni composti da più di dieci lati.
-
4Conta le diagonali che hai disegnato. Puoi scegliere due approcci: conti ogni diagonale che disegni oppure le tracci tutte e le conti alla fine. Se hai scelto di numerarle mentre le disegni, riporta un piccolo numero accanto a ciascuna di esse, in modo da non perdere il conto, dato che lavorando su poligoni con molti lati è molto facile confondersi.
- Nel caso di un quadrato le diagonali sono due: una per ogni coppia di angoli della figura.[7]
- Un esagono ha 9 diagonali: in questo caso ogni vertice del poligono dà origine a tre diagonali.
- Un ettagono ha ben 14 diagonali. Dopo l'ettagono risulta molto più difficile disegnare e contare le diagonali senza confondersi, dato che il numero di queste ultime è davvero elevato.
-
5Utilizzando questo metodo occorre fare molta attenzione a non contare la medesima diagonale due o più volte. Ogni vertice del poligono potrebbe dare origine a più diagonali, ma questo non significa che il numero totale delle diagonali sia dato dal prodotto del numero degli angoli per il numero di diagonali che partono da ciascuno. Assicurati di contare ogni diagonale una sola volta durante il conteggio totale.[8]
- Per esempio il pentagono (poligono composto da 5 lati) ha solo 5 diagonali. Ogni vertice dà origine a due diagonali, quindi se conti semplicemente tutte le diagonali che partono da ogni angolo potresti pensare che ne abbia dieci, ma commetteresti un errore. In questo caso sbaglieresti perché avresti contato ogni diagonale due volte anziché una sola.
-
6Fai pratica con alcuni esempi. Disegna altri poligoni e conta il numero di diagonali. Questo metodo funziona sia per i poligoni simmetrici sia per quelli asimmetrici. Nel caso dei poligoni concavi, potresti avere la necessità di tracciare alcune diagonali al di fuori dell'area della figura.[9]
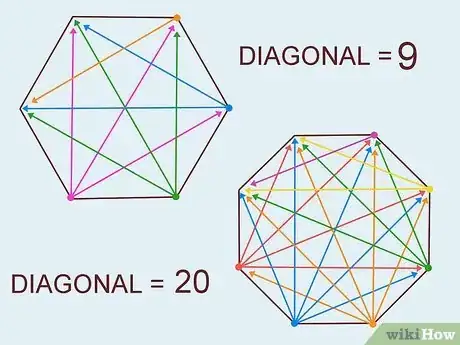
- Un esagono è caratterizzato da 9 diagonali.
- Un ottagono ha ben 20 diagonali.
Pubblicità
Usare la Formula Matematica per il Calcolo del Numero di Diagonali di un Poligono
-
1Definisci la formula. La formula che permette di calcolare matematicamente il numero di diagonali di un qualsiasi poligono è n(n-3)/2, dove "n" rappresenta il numero di lati della figura in esame.[10] Facendo ricorso alla proprietà distributiva dell'algebra, la medesima formula può essere riscritta nel seguente modo (n2 - 3n)/2. Anche se le due formule appaiono diverse il risultato finale è sempre il medesimo.
- La formula indicata è valida per calcolare il numero di diagonali di qualsiasi poligono.
- Nota: l'unica eccezione a questa regola è il triangolo, dato che non ha diagonali.[11]
-
2Individua il numero di lati del poligono in oggetto. Per poter utilizzare la formula indicata, hai la necessità di conoscere il numero totale dei lati che compongono il poligono in esame. Questa informazione basilare è racchiusa nel nome stesso del poligono, quindi devi solo conoscere il nome della figura che stai studiando. Di seguito sono riportati i prefissi dei nomi dei poligoni a cui devi fare riferimento per scoprire il numero di lati:[12]
- Tetra (4), penta (5), esa (6), etta (7), octa (8), enna (9), deca (10), endeca (11), dodeca (12), trideca (13), tetradeca (14), pentadeca (15), eccetera.
- Nel caso di poligoni con un numero di lati molto elevato, il nome potrebbe essere scritto nel seguente formato "n-gono", dove "n" rappresenta il numero di lati. Per esempio il nome di un poligono composto da 44 lati potrebbe essere scritto così: 44-gono.
- Se hai a disposizione un'immagine del poligono da studiare, puoi semplicemente contare manualmente il numero di lati che lo compongono.
-
3Sostituisci il numero dei lati all'interno dell'equazione per calcolare le diagonali. Adesso che conosci il numero di lati del poligono sostituiscilo alla variabile "n" della formula e svolgi i calcoli. Sostituisci tutte le variabili "n" dell'equazione con il numero dei lati del poligono in oggetto.[13]
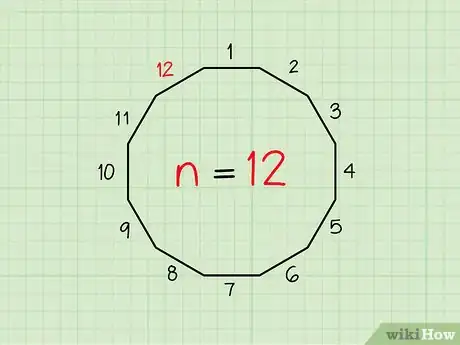
- Per esempio ipotizza di dover calcolare il numero di diagonali di un dodecagono che ha 12 lati;
- La formula di partenza è n(n-3)/2;
- Sostituendo le variabili con i dati otterrai (12(12 – 3))/2.
-
4Risolvi l'equazione. Il passaggio finale consiste nello svolgere i calcoli rispettando l'ordine corretto delle operazioni. Parti eseguendo la sottrazione, quindi calcola il prodotto e infine esegui la divisione. Il numero che otterrai corrisponderà al numero di diagonali del poligono in oggetto.[14]
- Proseguendo con l'esempio precedente dovrai risolvere il seguente calcolo: (12(12 – 3))/2;
- Eseguendo la sottrazione otterrai (12*9)/2;
- Eseguendo la moltiplicazione otterrai (108)/2;
- Eseguendo la divisione arriverai al risultato finale, cioè 54;
- A questo punto puoi affermare che un dodecagono ha 54 diagonali.
-
5Fai pratica con altri esempi. La pratica rende perfetti, quindi, per acquisire dimestichezza con l'applicazione di questa formula, non devi fare altro che continuare a usarla con altri poligoni di esempio. In questo modo avrai anche il vantaggio di poterla memorizzare nel caso ti dovesse servire durante un test di matematica, un esame o un quiz a premi. Ricorda che questa formula funziona per qualsiasi poligono composto da più di tre lati.
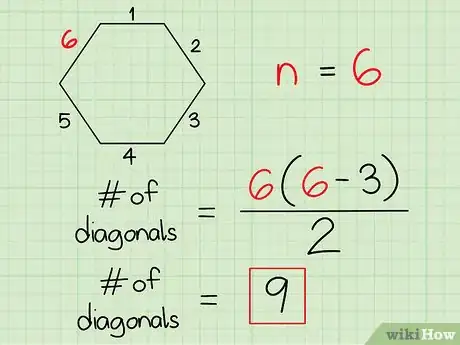
- Esagono (composto da 6 lati): n(n-3)/2 = 6(6-3)/2 = 6*3/2 = 18/2 = 9 diagonali.
- Decagono (composto da 10 lati): n(n-3)/2 = 10(10-3)/2 = 10*7/2 = 70/2 = 35 diagonali.
- Icosagono (composto da 20 lati): n(n-3)/2 = 20(20-3)/2 = 20*17/2 = 340/2 = 170 diagonali.
- 96-gono (composto da 96 lati): n(n-3)/2 = 96(96-3)/2 = 96*93/2 = 8928/2 = 4464 diagonali.
Pubblicità
Riferimenti
- ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html
- ↑ http://mathcentral.uregina.ca/QQ/database/QQ.09.96/rosa1.html
- ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html
- ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html
- ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html
- ↑ http://intermath.coe.uga.edu/tweb/CPTM1/trushin/diagonals/diagonalsinapolygon.htm
- ↑ http://intermath.coe.uga.edu/tweb/CPTM1/trushin/diagonals/diagonalsinapolygon.htm
- ↑ http://www.mathopenref.com/polygondiagonal.html
- ↑ https://www.mathsisfun.com/geometry/polygons-diagonals.html


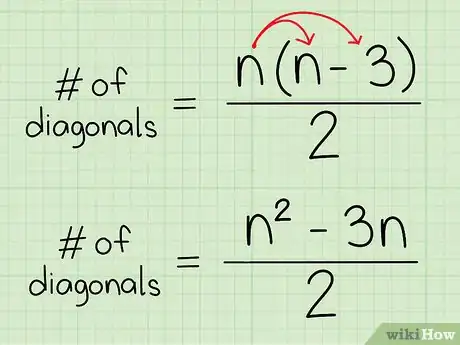

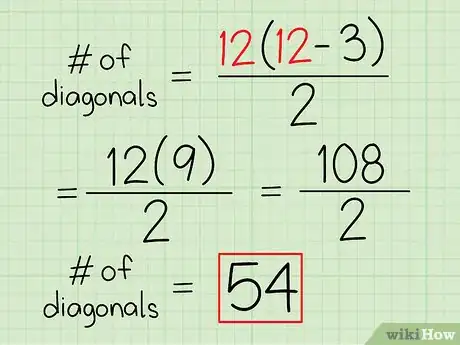




-to-Grams-(g)-Step-12-Version-4.webp)














