wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 13 092 volte
Trovare il punto centrale di un segmento è facile quando conosci le coordinate dei due punti estremi. Il modo più comune per farlo è di usare la formula del punto medio; c'è anche un altro modo per trovare il punto medio di un segmento quando è verticale o orizzontale. Se vuoi imparare a trovare il punto medio di un segmento in pochi minuti, segui i passaggi qui sotto.
Passaggi
Primo metodo: Usa la formula del punto medio
-
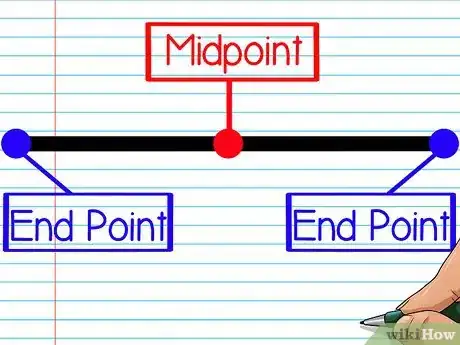
1Impara cosa è il punto medio. Il punto medio di un segmento è il punto che si trova esattamente nel punto di mezzo tra i due estremi. Si tratta, quindi, delle media dei due estremi, in altre parole la media delle due coordinate x e delle due coordinate y.
-
2Impara la formula del punto medio. La formula del punto medio può essere usata sommando le coordinate x dei due estremi e dividendo il risultato per due e poi sommando le coordinate y degli estremi e dividendo per due. Questa è la formula: [(x1 + x2)/2,( y1 + y2)/2]
-
3Localizza le coordinate degli estremi. Non è possibile usare la formula del punto medio senza conoscere le coordinate degli estremi. In questo esempio, si vuole trovare il punto medio, punto O, che si trova tra i due estremi M (5,4) e N (3,-4). Ne deriva che (x1, y1) = (5, 4) e (x2, y2) = (3, -4).
- Nota che entrambe le coppie di coordinate possono essere usate indifferentemente come (x1, y1) o (x2, y2), poiché stai solamente sommando le coordinate e dividendo per due, non importa quale coppia viene prima.
-
4Inserisci nella formula le coordinate corrispondenti. Ora che conosci le coordinate degli estremi, le puoi inserire nella formula. Ecco come fare:
- [(5 + 3)/2, (4 + -4)/2]
-
5Risolvi. Una volta sostituite le coordinate nella formula, dovrai solamente fare i calcoli per ottenere il punto medio. Ecco come fare:
- [(5 + 3)/2, (4 + -4)/2] =
- [(8/2), (0/2)] =
- (4, 0)
- Il punto medio degli estremi (5,4) e (3, -4) è (4,0).
Pubblicità
Secondo metodo: Trovare il punto medio di linee verticali o orizzontali
-
1Trova una linea verticale o orizzontale. Prima di usare questo metodo, dovrai imparare come individuare una linea verticale o orizzontale.
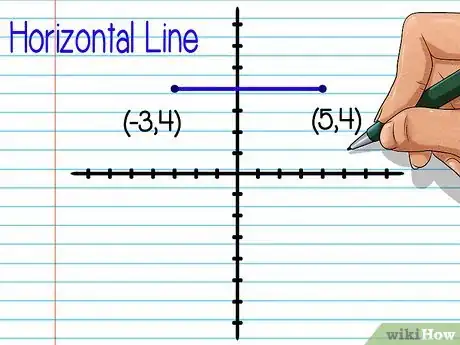
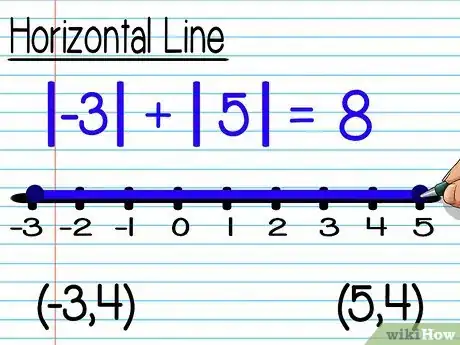
- Una linea è orizzontale se le due coordinate y degli estremi sono uguali. Per esempio, il segmento con gli estremi (-3, 4) e (5, 4) è orizzontale.
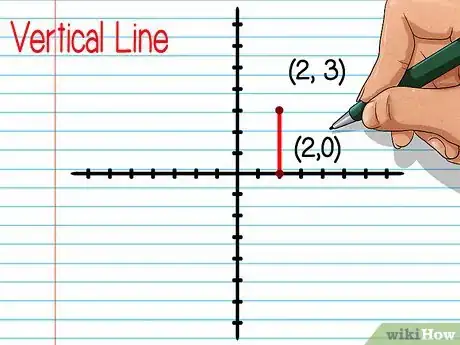
- Una linea è verticale se le due coordinate x degli estremi sono uguali. Per esempio, il segmento con gli estremi (2, 0) e (2, 3) è verticale.
-
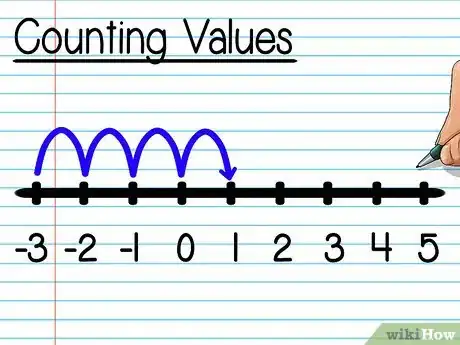
2Trova la lunghezza del segmento. Per trovare la lunghezza del segmento puoi contare gli spazi occupati in orizzontale o in verticale. Ecco come fare:
- Il segmento orizzontale aventi gli estremi (-3, 4) e (5, 4) ha una lunghezza di 8 unità. Lo puoi calcolare contando gli spazi occupati o sommando i valori assoluti delle coordinate x: |-3| + |5| = 8
- Il segmento verticale aventi gli estremi (2, 0) e (2, 3) ha una lunghezza di 3 unità. Lo puoi calcolare contando gli spazi occupati o sommando i valori assoluti delle coordinate y: |0| + |3| = 3
-
3
-
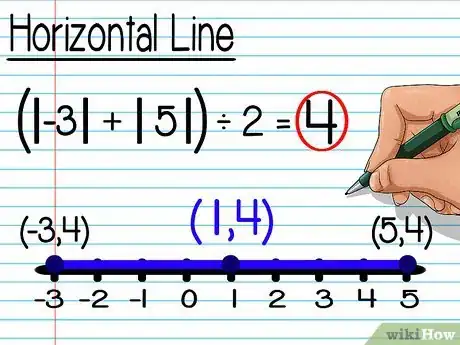
4Conta il valore da uno qualsiasi dei due estremi. Questo è l'ultimo passaggio per trovare l'estremo del segmento. Ecco come fare:
- Per trovare il punto medio dei punti (-3, 4) e (5, 4), spostati di 4 unità da destra o da sinistra per raggiungere il centro del segmento. (-3, 4) spostato di 4 sulla x è (1, 4). Non avrai bisogno di cambiare le coordinate y poiché il punto medio avrà la stessa y degli estremi. Il punto medio di (-3, 4) e (5, 4) è (1, 4).
- Per trovare il punto medio dei punti (2, 0) e (2, 3), spostati di 1,5 unità dall'alto o dal basso per raggiungere il centro del segmento. (2, 0) spostato in alto di 1,5 sarà (2, 1,5). Non avrai bisogno di cambiare le coordinate x poiché il punto medio avrà la stessa x degli estremi. Il punto medio di (2, 0) e (2, 3) è (2, 1.5).
Pubblicità
Cose che ti serviranno
- Matita
- Un foglio
- Righello
- Forbici
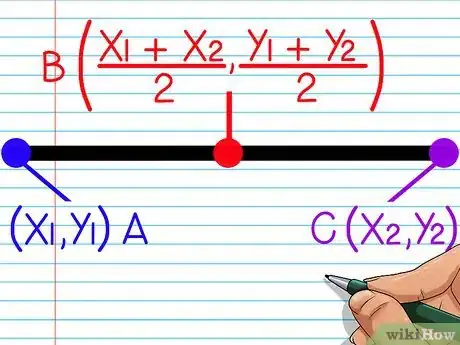
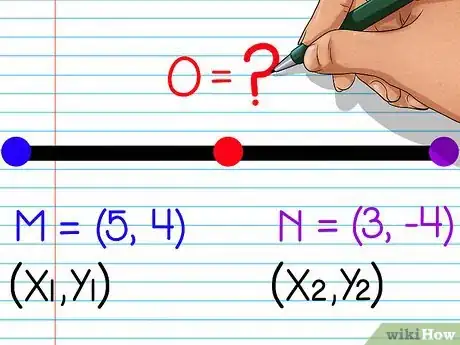

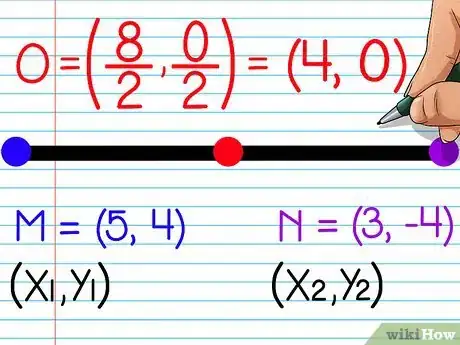








-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
