wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 15 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 76 188 volte
L’asse è la retta pendicolare al punto medio dei due estremi che individuano il segmanto. Per trovare la sua equazione, tutto quello che devi fare è trovare le coordinate del punto medio, la pendenza della retta che gli estremi intercettano e usare l’anti-reciproco per trovare la perpendicolare. Se vuoi sapere come trovare l’asse del segmento passante per due punti, basta seguire questi passaggi.
Passaggi
Raccolta di Informazioni
-
1Trova il punto medio dei due punti. Per trovare il punto medio di due punti, inseriscili semplicemente nella formula del punto medio: [(x1 + x2) / 2, (y1 + y2) / 2].Questo significa che stai trovando la media rispetto a ciascuna delle due coordinate di entrambi gli estremi, che conduce al punto medio.Supponiamo di stare lavorando con (x1, y 1) di coordinate di (2, 5) e (x2, y2) di coordinate (8, 3). Ecco come trovare il punto medio per quei due punti: [1]
- [(2 + 8) / 2, (5 + 3) / 2] =
- (10 / 2, 8 / 2) =
- (5, 4)
- Le coordinate del punto medio di (2, 5) e (8, 3) sono (5, 4).
-
2Trova la pendenza dei due punti: è sufficiente collegare i punti nella formula della pendenza:(y2 - y1) / (x2 - x1). La pendenza di una retta misura la variazione verticale rispetto a quella orizzontale. Ecco come trovare la pendenza della retta che passa per i punti (2, 5) e (8, 3): [2]
- (3 - 5) / (8 - 2) =
- -2 / 6 =
- -1 / 3
- Il coefficiente angolare della retta è -1 / 3. Per trovarlo, devi ridurre -2 / 6 ai suoi minimi termini, -1 / 3, dato che sia 2 sia 6 sono divisibili per 2.
-
3Trova il reciproco opposto di segno (anti-reciproco) della pendenza dei due punti: per trovarlo, basta prendere il reciproco e cambiare il segno. L’anti-reciproco di 1 / 2 è -2 / 1 o semplicemente -2; l’anti-reciproco di -4 è 1 / 4.[3]
- Il reciproco e opposto di -1 / 3 è 3, perché 3 / 1 è il reciproco di 1 / 3 e il segno è stato cambiato da negativo in positivo.
Pubblicità
Calcola l'Equazione della Retta
-
1Scrivi l'equazione di una retta di pendenza data. La formula è y = mx + b dove qualsiasi coordinata x e y della retta è rappresentata da "x" e "y", la "m" è la pendenza e "b" rappresenta l'intercetta, cioè dove la retta interseca l'asse y. Una volta scritta questa equazione, puoi cominciare a trovare quella dell’asse del segmento.[4]
-
2Inserisci l’anti-reciproco nell'equazione, che per i punti (2, 5) e (8, 3) era 3. La "m" nell'equazione rappresenta la pendenza, così metti 3 al posto della "m" nell'equazione y = mx + b.
- 3 —> y = mx + b
- y = 3 x + b
-
3Sostituisci le coordinate del punto medio del segmento. Sai già che il punto medio dei punti (2, 5) e (8, 3) è (5, 4). Poiché l’asse del segmento passa attraverso il punto medio dei due estremi, è possibile inserire le coordinate del punto medio nell'equazione della retta. Molto semplicemente, sostituisci (5, 4) rispettivamente nella x e nella y.
- (5, 4) —-> y = 3 x + b
- 4 = 3 * 5 + b
- 4 = 15 + b
-
4Trova l'intercetta. Hai trovato tre delle quattro variabili nell'equazione della retta. Ora hai abbastanza informazioni per risolvere secondo la variabile rimanente, "b", che è l'intercetta di questa retta lungo y. Isola la variabile "b" per trovare il suo valore. Basta sottrarre 15 da entrambi i lati dell'equazione.
- 4 = 15 + b
- -11 = b
- b = -11
-
5Scrivi l'equazione dell’asse del segmento. Per scriverla, devi semplicemente inserire la pendenza (3) e l'intercetta (-11) nell'equazione di una retta. I valori non devono essere inseriti al posto della x e della y.
- y = mx + b
- y = 3 x - 11
- L'equazione dell’asse del segmento di estremi (2, 5) e (8, 3) è y = 3 x - 11.
Pubblicità
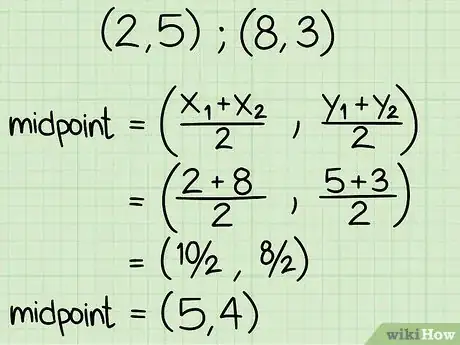


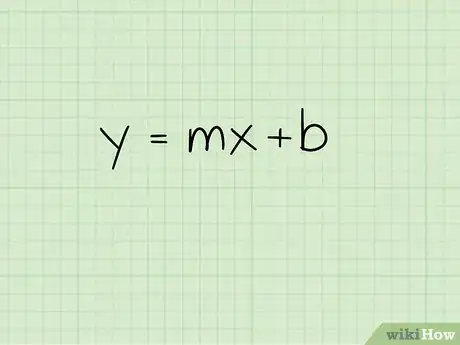
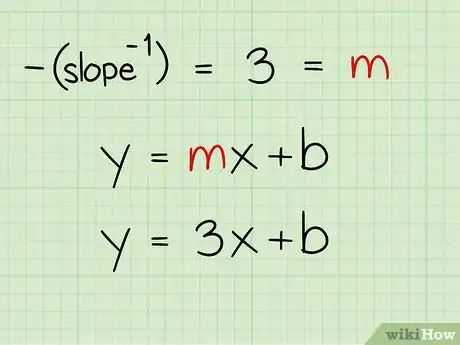
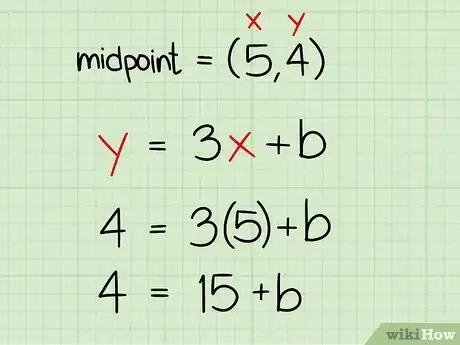
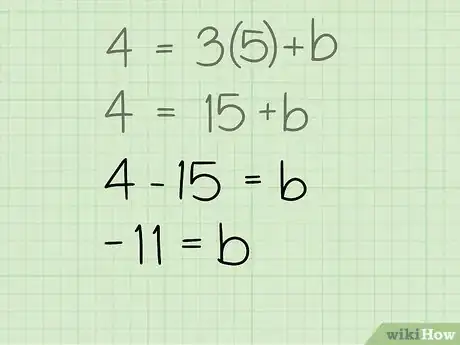
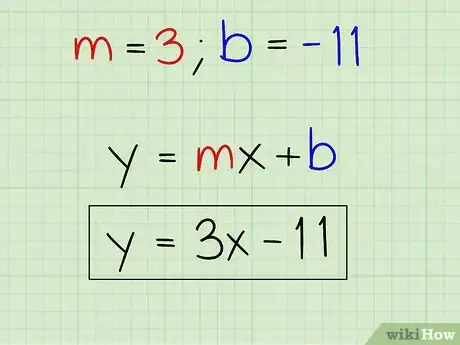



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
