wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 20 512 volte
Il grafico di un polinomio o di una funzione rivela molte caratteristiche che non sarebbero chiare senza una rappresentazione visuale del grafico. Una di queste caratteristiche è l'asse di simmetria: una linea verticale che divide il grafico in due immagini speculari e simmetriche. Trovare l'asse di simmetria per un dato polinomio è abbastanza semplice. Ecco i due metodi fondamentali.
Passaggi
Trovare l'Asse di Simmetria per i Polinomi di Secondo Grado
-
1Verifica il grado del polinomio. Il grado (o "ordine") di un polinomio è semplicemente l'esponente più alto dell'espressione. Se il grado del polinomio è 2 (ovvero non vi è alcun esponente più alto di x2), puoi trovare l'asse di simmetria usando questo metodo. Se il grado del polinomio è superiore a due, usa il Metodo 2.
- Per illustrare questo metodo, prendiamo ad esempio il polinomio 2x2 + 3x – 1. L'esponente più alto presente è x2, quindi è un polinomio di secondo grado ed è possibile usare il primo metodo per trovare l'asse di simmetria.
-
2Inserisci i numeri nella formula per trovare l'asse di simmetria. Per calcolare l'asse di simmetria di un polinomio di secondo grado nella forma ax2 + bx +c (una parabola), adopera la formula x = -b / 2a.
- Nell'esempio dato, a = 2, b = 3, e c = -1. Inserisci questi valori nella formula e otterrai:
x = -3 / 2(2) = -3/4.
- Nell'esempio dato, a = 2, b = 3, e c = -1. Inserisci questi valori nella formula e otterrai:
-
3Scrivi l'equazione dell'asse di simmetria. Il valore calcolato con la formula dell'asse di simmetria è l'intersezione dell'asse di simmetria con l'asse delle ascisse.
- Nell'esempio dato, l'asse di simmetria è -3/4.
Pubblicità
Trovare Graficamente l'Asse di Simmetria
-
1Verifica il grado del polinomio. Il grado (o "ordine") di un polinomio è semplicemente l'esponente più alto dell'espressione. Se il grado del polinomio è 2 (ovvero non vi è alcun esponente più alto di x2), puoi trovare l'asse di simmetria usando il metodo sopra descritto. Se il grado del polinomio è superiore a due, usa il metodo grafico seguente.
-
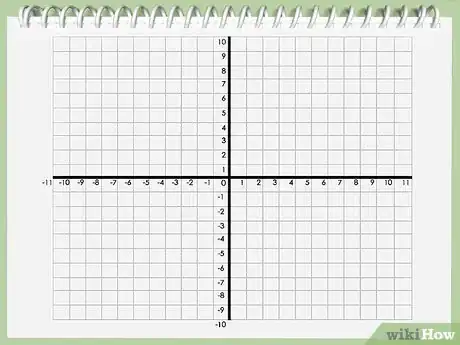
2Disegna gli assi x e y. Traccia due linee in modo da formare una sorta di segno "più" o una croce. La linea orizzontale è l'asse delle ascisse, o asse x; la linea verticale è l'asse delle ordinate, o asse y.
-
3Numera il grafico. Contrassegna entrambi gli assi con i numeri ordinati a intervalli regolari. La distanza tra i numeri deve essere uniforme su entrambi gli assi.
-
4Calcola y = f(x) per ogni x. Prendi in considerazione la funzione o il polinomio e calcola i valori di f(x) inserendovi i valori di x.
-
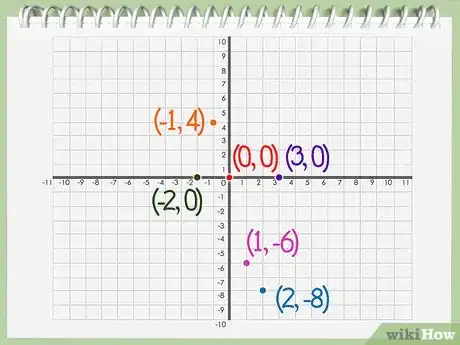
5Per ogni coppia di coordinate individua il punto corrispondente nel grafico. Adesso hai coppie di y = f(x) per ogni x presente sull'asse. Per ogni coppia di coordinate (x, y), individua un punto sul grafico – verticalmente sull'asse x e orizzontalmente sull'asse y.
-
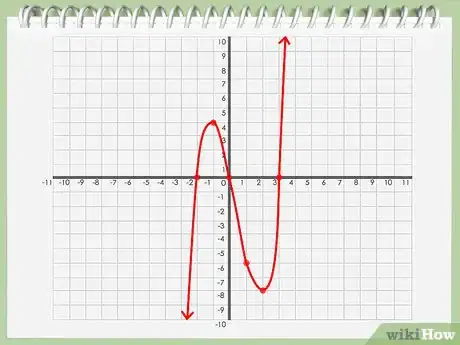
6Traccia il grafico del polinomio. Dopo aver individuato tutti i punti sul grafico, collegali con una linea regolare e continua per evidenziare l'andamento del grafico del polinomio.
-
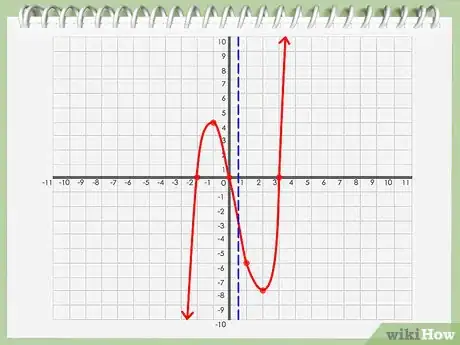
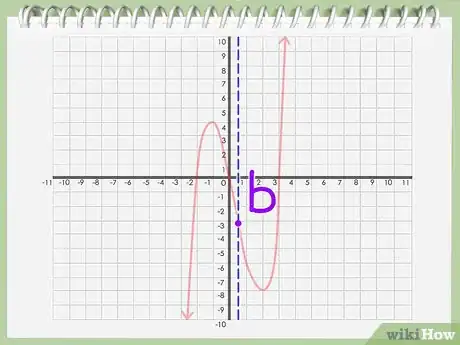
7Cerca l'asse di simmetria. Osserva attentamente il grafico. Cerca sull'asse un punto tale che, se una linea lo attraversa, il grafico si divida in due metà uguali e speculari.
-
8Individua l'asse di simmetria. Se hai trovato un punto – chiamiamolo “b” – sull'asse x, tale che il grafico si divida in due metà speculari, allora quel punto "b" è l'asse di simmetria.Pubblicità
Consigli
- La lunghezza degli assi delle ascisse e delle ordinate dovrebbe essere tale da permettere una visione chiara del grafico.
- Alcuni polinomi non sono simmetrici. Per esempio, y = 3x non ha un asse di simmetria.
- La simmetria di un polinomio può essere classificata in simmetria pari o dispari. Qualsiasi grafico che presenta un asse di simmetria sull'asse y ha una simmetria "pari"; qualsiasi grafico che presenta un asse di simmetria sull'asse x ha una simmetria "dispari".
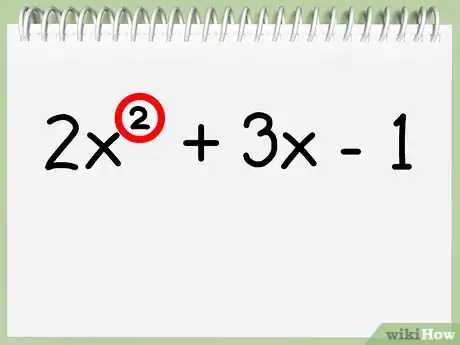
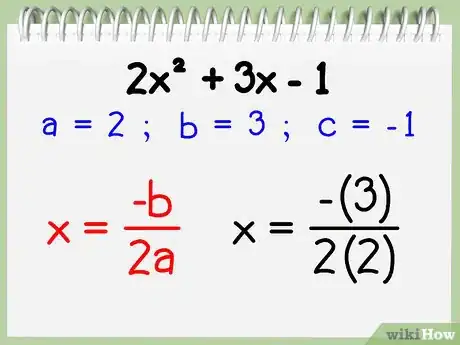
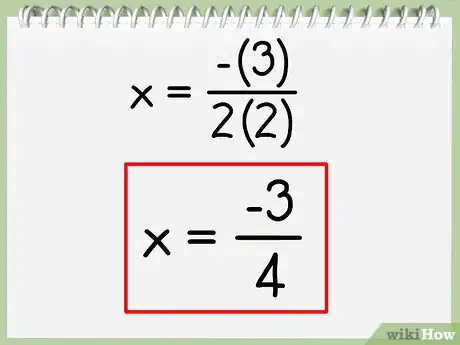
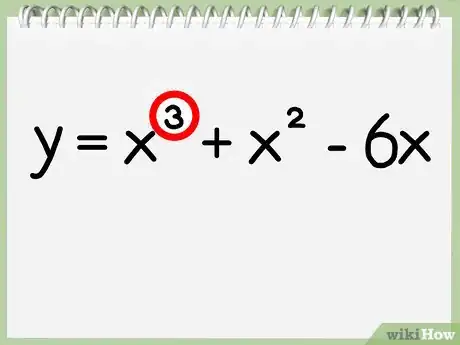





-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
