Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 8 582 volte
La proprietà distributiva stabilisce che il prodotto di un numero per una somma è uguale alla somma dei singoli prodotti del numero per ciascuno degli addendi. Questo significa che a(b + c) = ab + ac. Puoi utilizzare questa proprietà fondamentale per risolvere e semplificare svariati tipi di equazioni. Se vuoi sapere come utilizzare la proprietà distributiva per risolvere un'equazione, basta seguire i seguenti passaggi.
Passaggi
Come Usare la Proprietà Distributiva: Caso Elementare
-
1Moltiplica il termine che sta fuori dalle parentesi con i termini che stanno dentro le parentesi. Nel fare questo, stai sostanzialmente distribuendo il termine che è fuori delle parentesi in quelli che stanno dentro. Moltiplica il termine esterno per il primo dei termini interni e poi per il secondo. Se ce ne sono più di due, continua ad applicare la proprietà moltiplicando per i restanti termini. Ecco come fare:
- Es: 2(x - 3) = 10
- 2(x) - (2)(3) = 10
- 2x - 6 = 10
-
2Somma i termini simili. Prima di risolvere l'equazione dovrai sommare i termini simili. Somma tutti i termini numerici e tutti i termini che contengono la "x". Sposta tutti i termini numerici alla destra dell'uguale e tutti i termini con la "x" alla sinistra.
- 2x - 6(+6) = 10 (+6)
- 2x = 16
-
3Risolvi l'equazione. Trova il valore della "x" dividendo entrambi i termini dell'equazione per 2.
- 2x = 16
- 2x/2 = 16/2
- x = 8
Pubblicità
Come Usare la Proprietà Distributiva: Caso Più Avanzato
-
1Moltiplica il termine che sta fuori delle parentesi con i termini che stanno dentro le parentesi. Questo passaggio è lo stesso che abbiamo fatto nel caso base, ma in questo caso utilizzerai la proprietà distributiva più di una volta nella stessa equazione.
- Es: 4(x + 5) = 8 + 6(2x - 2)
- 4(x) + 4(5) = 8 + 6(2x) - 6(2)
- 4x + 20 = 8 +12x -12
-
2Somma i termini simili. Somma tutti i termini simili e spostali in modo che tutti i termini che contengono la x stiano alla sinistra dell'uguale e tutti i termini numerici stiano alla destra .
- 4x + 20 = 8 +12x -12
- 4x + 20 = 12x - 4
- 4x -12x = -4 - 20
- -8x = -24
-
3Risolvi l'equazione. Trova il valore della "x" dividendo entrambi i termini dell'equazione per -8.
- -8x/-8 = -24/-8
- x = 3
Pubblicità
Come Applicare la Proprietà Distributiva con un Coefficiente Negativo
-
1Moltiplica il termine che sta fuori delle parentesi con i termini che stanno dentro. Se esso ha segno negativo, semplicemente distribuisci anche il segno. Se stai moltiplicando un numero negativo per uno positivo, il risultato sarà negativo; se stai moltiplicando un numero negativo per un altro numero negativo, il risultato sarà positivo.
- Es: -4(9 - 3x) = 48
- -4(9) - [-4(3x)] = 48
- -36 -(-12x) = 48
- -36 + 12x = 48
-
2Somma i termini simili. Sposta tutti i termini con la "x" alla sinistra dell'uguale e tutti i termini numerici alla destra.
- -36 + 12x = 48
- 12x = 48 - [-(36)]
- 12x = 84
-
3Risolvi l'equazione. Trova il valore della "x" dividendo entrambi i termini dell'equazione per 12.
- 12x/12 = 84/12
- x = 7
Pubblicità
Come Semplificare i Denominatori in un Equazione
-
1Trova il minimo comune multiplo (mcm) dei denominatori delle frazioni presenti nell'equazione. Per trovare il mcm, devi trovare il numero più piccolo che sia multiplo di tutti i denominatori delle frazioni dell'equazione. I denominatori sono 3 e 6; 6 è il numero più piccolo che è multiplo sia di 3 che di 6.
- x - 3 = x/3 + 1/6
- mcm = 6
-
2Moltiplica i termini dell'equazione per il mcm. Adesso metti fra parentesi tutti i termini che stanno a sinistra dell'equazione e fa la stessa cosa per quelli che stanno a destra, e metti il mcm fuori delle parentesi. Poi moltiplica, applicando, se necessario, la proprietà distributiva. Moltiplicare entrambi i termini delle parentesi per lo stesso numero trasforma l'equazione in una equivalente, cioè in un'altra equazione che ha lo stesso risultato, ma ha dei numeri con cui è più facile eseguire i calcoli dopo che avrai semplificato le frazioni.
- 6(x - 3) = 6(x/3 + 1/6)
- 6(x) - 6(3) = 6(x/3) + 6(1/6)
- 6x - 18 = 2x + 1
-
3Somma i termini simili. Sposta tutti i termini con la "x" alla sinistra dell'uguale e tutti i termini numerici alla destra.
- 6x - 2x = 1 - (-18)
- 4x = 19
-
4Risolvi l'equazione. Trova il valore della "x" dividendo entrambi i termini per 4.
- 4x/4 = 19/4
- x = 19/4 oppure (16+3)/4
Pubblicità
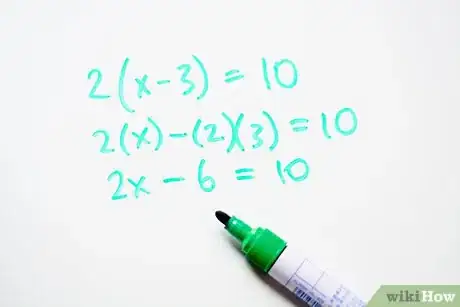
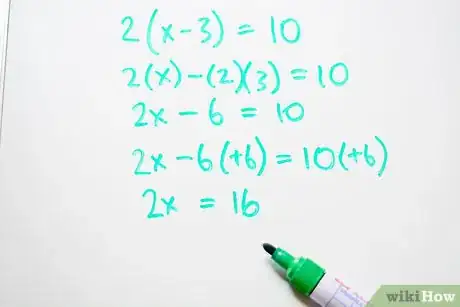
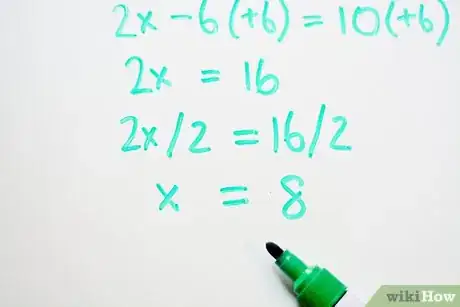
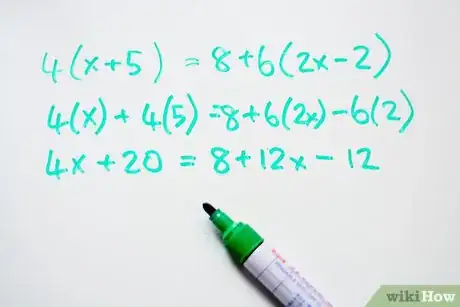
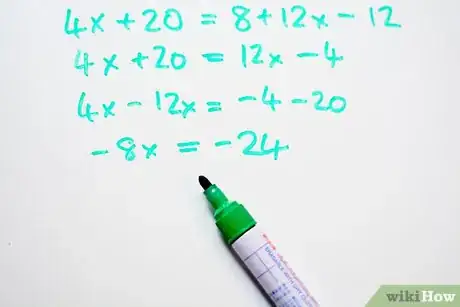
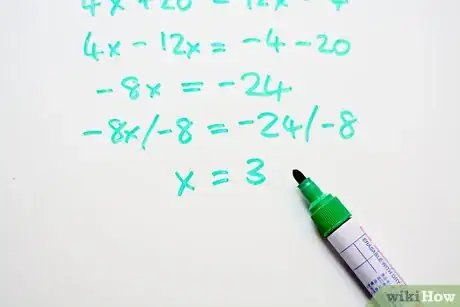
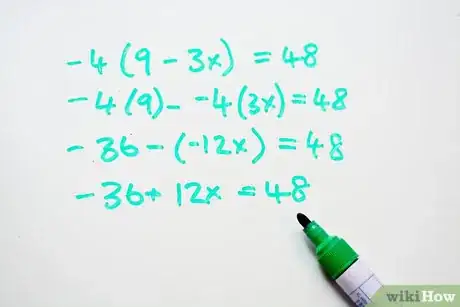
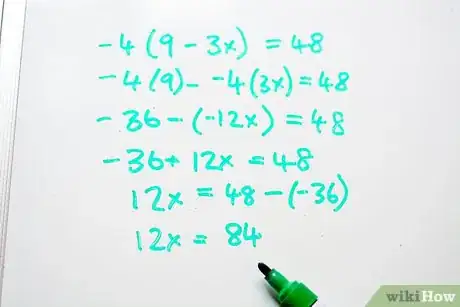
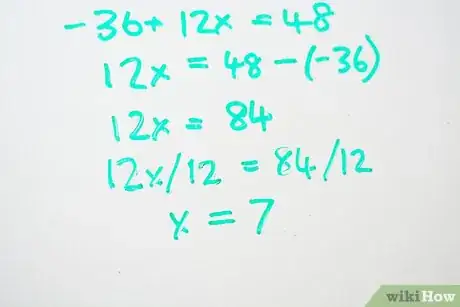
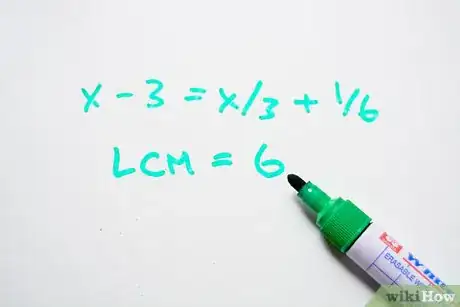
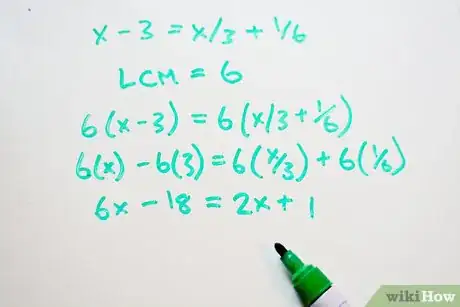
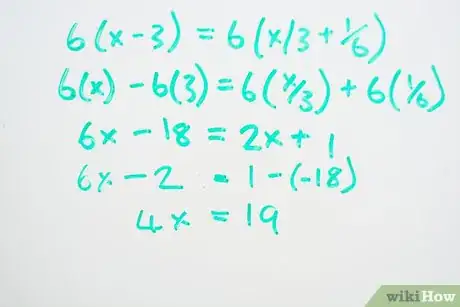
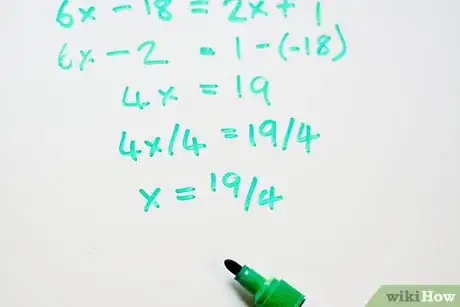



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 8 582 volte