Come Calcolare il Volume di un Prisma a Base Triangolare

Co-redatto da Lo Staff di wikiHow

È facile supporre che si possa calcolare il volume di un prisma triangolare nello stesso modo in cui si calcola quello di una piramide. Tuttavia un prisma a base triangolare è un poliedro composto da tre facce e due basi identiche a forma di triangolo. Per calcolare il volume di questo tipo di solido occorre per prima cosa ricavare l'area della base triangolare e poi moltiplicare il risultato per l'altezza del prisma.

Parte 1

Parte 1 di 2:

Calcolare l'Area della Base Triangolare

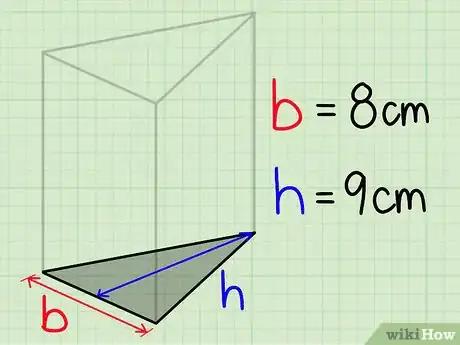
1
Ricava la misura della base e dell'altezza del triangolo che rappresenta la base del prisma. Esamina il triangolo e prendi nota della lunghezza della base e dell'altezza. Per esempio ipotizza di avere un triangolo con base di 8 cm e altezza di 9 cm.^{[1]
X
Fonte di ricerca}
- Ricorda che in questo caso vuoi ricavare l'altezza del triangolo che rappresenta la base del prisma, non l'altezza di quest'ultimo.
- Puoi usare indifferentemente le dimensioni di una qualsiasi delle due basi triangolari del prisma, dato che sono perfettamente identiche.
2
Inserisci i valori ottenuti all'interno della formula matematica per il calcolo dell'area di un triangolo. Dopo aver ricavato la misura della base e dell'altezza del triangolo in esame puoi calcolarne l'area utilizzando l'apposita formula matematica:^{[2]
X
Fonte di ricerca}
- Area = 1/2 x Base x Altezza. Normalmente questa formula viene scritta nel seguente modo $A={\frac {1}{2}}bh$
3
Per ottenere l'area di un triangolo moltiplica la base per l'altezza e dividi il risultato ottenuto a metà; in questo modo avrai la misura dell'area della base triangolare del prisma in esame. Ricorda di esprimere il risultato con un'unità di misura quadrata, dato che stai calcolando la dimensione di una superficie.^{[3]
X
Fonte di ricerca}
- Per esempio se la base è lunga 8 cm e l'altezza misura 9 cm, la formula per calcolare l'area di questo triangolo avrà il seguente aspetto $A={\frac {1}{2}}*8*9$ . L'area di questo triangolo di esempio sarà quindi pari a 36 cm².
Pubblicità

Parte 2

Parte 2 di 2:

Calcolare il Volume del Prisma

1
Inserisci il valore dell'area del triangolo all'interno della formula matematica per il calcolo del volume di un prisma triangolare. L'area della base di un prisma triangolare è uno dei due dati che servono per poterne calcolare il volume. La formula matematica è la seguente $V=Area_{B}ase*h$ $V=Area_{B}ase*h$ .^{[4]
X
Fonte di ricerca}
- Utilizzando le informazioni dell'esempio precedente, la formula per calcolare il volume del prisma assumerà questo aspetto: $V=36*h$ .
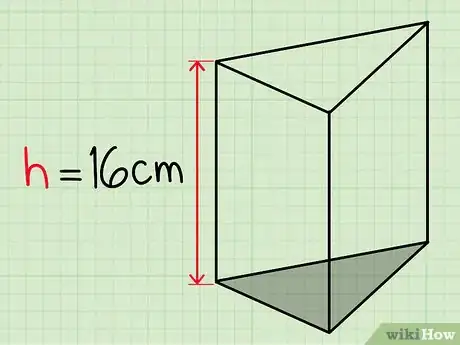
2
Ricava l'altezza del prisma e inserisci il valore all'interno della formula. Arrivato a questo punto, per ottenere la soluzione al tuo problema devi semplicemente calcolare o misurare l'altezza del prisma in esame che corrisponde alla lunghezza di uno dei lati delle facce del solido. Ipotizza per esempio che l'altezza del solido sia pari a 16 cm. Inserisci questo valore all'interno della formula $V=Area_{B}ase*h$ $V=Area_{B}ase*h$ .^{[5]
X
Fonte di ricerca}
- Proseguendo con l'esempio precedente, la formula dovrebbe avere il seguente aspetto $V=36*16$ .
3
Moltiplica l'area della base triangolare per l'altezza del prisma e otterrai il volume del solido. Dato che a questo punto sei in possesso di tutti i dati che ti servono, per risolvere il problema non ti resta che eseguire i calcoli. In questo modo otterrai il volume del prisma triangolare in esame.^{[6]
X
Fonte di ricerca}
- Proseguendo con l'esempio precedente otterrai che il volume è pari a $V=36*16$ , cioè 576 cm³.
Pubblicità

Consigli

Prima di svolgere i calcoli, assicurati che tutti i dati siano espressi con le medesime unità di misura. Per esempio, se una misura del prisma è espressa in millimetri, mentre tutte le altre in centimetri, dovrai eseguirne la conversione da millimetri a centimetri prima di poter eseguire i calcoli correttamente; in caso contrario otterresti dei risultati errati.