Questo articolo è stato co-redatto da Mario Banuelos, PhD. Mario Banuelos lavora come assistente universitario di matematica alla California State University - Fresno. Con oltre otto anni di esperienza nell'insegnamento, è specializzato in biologia teorica, ottimizzazione, modelli statistici per l'evoluzione del genoma e scienza dei dati. Si è laureato in matematica presso la California State University - Fresno e ha realizzato un dottorato di ricerca in Matematica Applicata alla University of California - Merced. Ha insegnato sia alle scuole superiori sia a livello universitario.
Ci sono 7 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 242 305 volte
La varianza è un indicatore della variabilità di un insieme di dati. Un valore basso significa che i dati sono raggruppati molto vicini fra loro, mentre una varianza elevata indica dei dati più distribuiti. Questo è un concetto che ha molte applicazioni in statistica. Ad esempio, il confronto della varianza di due insiemi di dati (come i pazienti maschi e femmine) è un modo per capire quale variabile produce un effetto evidente.[1] La varianza si rivela utile anche quando si creano dei modelli statistici, poiché, quando è bassa, indica un campione troppo raggruppato.[2]
Passaggi
Calcolare la Varianza di un Campione
-
1Scrivi i dati che compongono il campione. Nella maggioranza dei casi, gli studiosi di statistica hanno accesso solo a un campione o a un gruppo della popolazione che stanno analizzando. Ad esempio, invece di analizzare l'insieme globale del "costo di ogni automobile in Germania", uno studioso calcola quello di un campione casuale composto da poche migliaia di vetture. In questo modo, potrà utilizzare il campione per stimare i costi delle macchine in Germania, anche se il valore non coinciderà esattamente con i numeri reali.
- Esempio: analizzando il numero di cornetti venduti ogni giorno in una caffetteria, ottieni questo campione casuale raccolto in sei giorni: 17; 15; 23; 7; 9; 13. Questo è solo un campione e non una popolazione, dato che non possiedi i dati di vendita di ogni singolo giorno in cui il bar è stato aperto.
- Se possiedi tutti i dati della popolazione, passa direttamente al metodo successivo.
-
2Scrivi la formula per la varianza di un campione. Questo valore ti darà un'idea della distribuzione dei dati. Più la varianza si avvicina allo zero e più i dati sono raggruppati fra loro. Quando lavori con un campione, usa la seguente formula:[3]
- = ∑[( - x̅)]/(n – 1);
- è la varianza che viene sempre misurata in unità al quadrato;
- rappresenta un dato del campione;
- ∑ significa "sommatoria" e indica che devi calcolare i termini successivi per ogni valore di e poi sommarli fra loro;
- x̅ è il valore medio del campione;
- n è il numero dei dati che compongono l'insieme.
-
3Calcola la media del campione. Il simbolo x̅ indica la media dell'insieme di dati.[4] Procedi al calcolo come faresti normalmente: somma tutti i valori fra loro e dividi per il numero dei dati.
-
Esempio: per prima cosa, somma tutti i dati che compongono il campione; quindi: 17 + 15 + 23 + 7 + 9 + 13 = 84
In seguito, dividi il risultato per il numero dei valori, che in questo caso è pari a 6: 84 ÷ 6 = 14.
La media del campione è x̅ = 14. - Puoi considerare la media come il "punto centrale" del campione. Se i dati si raggruppano attorno alla media, significa che la varianza è bassa. Se i valori si allontanano e sono molto distribuiti attorno alla media, allora la varianza è alta.
-
Esempio: per prima cosa, somma tutti i dati che compongono il campione; quindi: 17 + 15 + 23 + 7 + 9 + 13 = 84
-
4Sottrai la media da ogni valore che compone l'insieme. Ora è giunto il momento di procedere a questo calcolo - x̅, dove rappresenta ogni dato che compone il campione. Ogni differenza ti informa della deviazione del dato dalla media o, in altri termini, di quanto il valore si allontana dalla media.[5] .
-
Esempio:
- x̅ = 17 - 14 = 3
- x̅ = 15 - 14 = 1
- x̅ = 23 - 14 = 9
- x̅ = 7 - 14 = -7
- x̅ = 9 - 14 = -5
- x̅ = 13 - 14 = -1. - Non è difficile controllare i calcoli, dato che la somma dei risultati deve dare zero. Questo fenomeno è dovuto alla definizione stessa del valore medio, poiché i valori negativi (la distanza della media dai numeri minori) devono annullare perfettamente i valori positivi (la distanza della media dai numeri maggiori).
-
Esempio:
-
5Eleva al quadrato ogni risultato. Come già indicato in precedenza, la somma delle deviazioni ( - x̅) è pari a zero. Questo significa che la "deviazione media" deve essere pari a zero e quindi non fornisce alcuna ulteriore informazione sulla distribuzione del campione. Per eliminare questo problema, trova il quadrato di ciascuna deviazione. In tal modo, otterrai solo valori positivi e quelli negativi non potranno annullare gli altri.[6]
-
Esempio:
( - x̅)
- x̅)
92 = 81
(-7)2 = 49
(-5)2 = 25
(-1)2 = 1; - Ora hai il valore ( - x̅) per ogni dato del campione.
-
Esempio:
-
6Trova la somma dei quadrati. A questo punto devi calcolare il numeratore della formula: ∑[( - x̅)]. La lettera greca maiuscola sigma, ∑, indica che devi sommare tutti i valori che il termine successivo assume per ogni . Hai già calcolato ( - x̅) per ogni valore di del campione, quindi quello che devi fare è procedere a una semplice somma.
- Esempio: 9 + 1 + 81 + 49 + 25 + 1 = 166.
-
7Dividi il risultato per n - 1, dove n è il numero dei dati dell'insieme. In passato, gli studiosi di statistica si limitavano a dividere per n durante il calcolo della varianza. In questo modo, ottenevano il valore medio della deviazione standard che combacia perfettamente con la varianza del campione. Tuttavia, devi ricordare che il campione è solo una stima di una popolazione maggiore. Se consideri un altro campione casuale ed esegui i medesimi calcoli, troverai risultati diversi. Per questa ragione, dividere per n - 1 al posto di n fornisce una stima migliore della varianza di una popolazione più grande, che è ciò che interessa davvero agli statistici. Questa correzione è così comune e ampiamente accettata che fa parte della definizione di varianza.[7]
-
Esempio: ci sono sei dati nel campione, quindi n = 6.
La varianza del campione è = 33,2.
-
Esempio: ci sono sei dati nel campione, quindi n = 6.
-
8Comprendi la varianza e la deviazione standard. Poiché c'è una potenza al numeratore, ricorda che la varianza viene espressa con l'unità di misura originale al quadrato. Ciò rende difficile intuire rapidamente il suo significato; a questo scopo, si utilizza maggiormente la deviazione standard. Non hai sprecato tutti gli sforzi fatti finora, dato che la deviazione standard si definisce come la radice quadrata della varianza. Questo è il motivo per cui la varianza di un campione viene espressa come , mentre la deviazione standard come .
- Ad esempio, la deviazione standard del campione preso precedentemente in esame è s = √33,2 = 5,76.
Pubblicità
Calcolare la Varianza di una Popolazione
-
1Considera una popolazione di dati. Il termine "popolazione" si riferisce all'intero gruppo preso in esame. Ad esempio, se stai studiando l'età dei residenti in Veneto, la popolazione statistica prevede i dati dell'età di ogni singola persona che vive in questa regione. In genere, si crea un foglio di calcolo per questo tipo di analisi su larga scala, ma puoi procedere anche con un insieme più piccolo:
-
Esempio: ci sono esattamente 6 vasche nella stanza dell'acquario municipale. Queste 6 vasche contengono le seguenti quantità di pesci:
.
-
Esempio: ci sono esattamente 6 vasche nella stanza dell'acquario municipale. Queste 6 vasche contengono le seguenti quantità di pesci:
-
2Scrivi la formula della varianza di una popolazione. Dato che una popolazione contiene tutti i dati di cui hai bisogno, la formula ti permette di calcolare l'esatta varianza della popolazione e non una stima. Per distinguerla da quella del campione (che è appunto solo una stima), gli statistici usano delle variabili diverse:[8]
- σ = (∑( - μ))/n;
- σ = è la varianza della popolazione. Si tratta della lettera greca minuscola sigma al quadrato. La varianza si esprime in unità di misura quadratiche;
- rappresenta un termine dell'insieme di dati;
- I termini compresi in ∑ saranno calcolati per ogni valore di e poi sommati;
- μ è la media della popolazione;
- n è il numero dei valori che compongono la popolazione.
-
3Trova la media della popolazione. Quando analizzi un intero gruppo di dati, il simbolo μ ("mu") rappresenta la media aritmetica. Per calcolarla, somma fra loro tutti i valori e poi dividili per il numero dei dati.
- Potresti pensare che la media sia anche il valore medio, ma fai attenzione, perché questo termine ha diverse definizioni in matematica.
- Esempio: media = μ = = 10,5.
-
4Sottrai la media da ogni valore che compone la popolazione. Se i valori sono vicini alla media, la differenza sarà prossima allo zero. Ripeti la sottrazione per ogni dato della popolazione e comincerai a capirne la distribuzione.
-
Esempio:
- μ = 5 – 10,5 = -5,5
- μ = 5 – 10,5 = -5,5
- μ = 8 – 10,5 = -2,5
- μ = 12 – 10,5 = 1,5
- μ = 15 – 10,5 = 4,5
- μ = 18 – 10,5 = 7,5.
-
Esempio:
-
5Eleva al quadrato ogni risultato. A questo punto, alcuni dei valori calcolati in precedenza saranno negativi e altri positivi. Se disponi i dati su una linea di numeri, questi gruppi rappresenteranno i numeri che si trovano a sinistra e a destra della media. Tutto ciò non è di aiuto per calcolare la varianza, dato che tali valori si annullano reciprocamente. Elevali al quadrato per ottenere solo dati positivi.
-
Esempio:
( - μ) per ogni valore di i da 1 a 6:
(-5,5) = 30,25
(-5,5) = 30,25
(-2,5) = 6,25
(1,5) = 2,25
(4,5) = 20,25
(7,5) = 56,25.
-
Esempio:
-
6Trova la media dei risultati. Ora hai il valore per ogni dato, correlato (indirettamente) a quanto si allontana dalla media. Calcolane la media sommandoli e poi dividendo il risultato per il numero dei dati.
-
Esempio:
Varianza della popolazione = 24,25.
-
Esempio:
-
7Collega questo risultato alla formula. Se non sei sicuro che corrisponda alla formula descritta all'inizio del metodo, riscrivi per esteso tutta l'equazione:
- Dopo aver calcolato la differenza dalla media e averla elevata al quadrato, hai il valore ( - μ), ( - μ) e così via fino a ( - μ), dove è l'ultimo dato della popolazione.
- Per trovare la media di questi valori, sommali fra loro e dividi per n: ( ( - μ) + ( - μ) + ... + ( - μ) ) / n
- Dopo avere riscritto il numeratore con la notazione di sigma otterrai: (∑( - μ))/n, cioè la formula della varianza.
Pubblicità
Consigli
- Poiché l'interpretazione della varianza è piuttosto difficile, si calcola solitamente come punto di partenza per ottenere la deviazione standard.
- Durante l'analisi dei campioni, l'utilizzo di "n-1" al posto di "n" al denominatore è chiamato correzione di Bessel. Il campione rappresenta solo una stima della popolazione completa e la media del campione si adatta solo parzialmente a questa stima. La correzione permette di eliminare tale imprecisione. Questo stimatore è correlato al fatto che, quando si elencano n-1 punti, il punto finale n-esimo è obbligato, perché solo certi valori risulteranno nella media del campione (x̅) usata nella formula della varianza.[9]
Riferimenti
- ↑ http://sphweb.bumc.bu.edu/otlt/MPH-Modules/BS/BS704_HypothesisTesting-ANOVA/BS704_HypothesisTesting-Anova_print.html
- ↑ http://insidebigdata.com/2014/10/22/ask-data-scientist-bias-vs-variance-tradeoff/
- ↑ https://www.youtube.com/watch?v=VgKHjVDK0uM
- ↑ http://stattrek.com/statistics/notation.aspx
- ↑ http://www.mathsisfun.com/data/standard-deviation.html
- ↑ https://www.youtube.com/watch?v=sOb9b_AtwDg
- ↑ https://www.youtube.com/watch?v=sOb9b_AtwDg
- ↑ https://www.youtube.com/watch?v=VgKHjVDK0uM
- ↑ http://www.statsdirect.com/help/default.htm#basics/degrees_freedom.htm
Informazioni su questo wikiHow
Per calcolare la varianza, inizia calcolando la media del tuo campione. Poi sottrai la media da ciascun elemento ed eleva al quadrato le differenze. In seguito somma tutte le differenze al quadrato. Infine dividi la somma per n meno 1, in cui n è uguale al totale degli elementi del campione. Per imparare a calcolare la varianza di una popolazione, continua a leggere!




































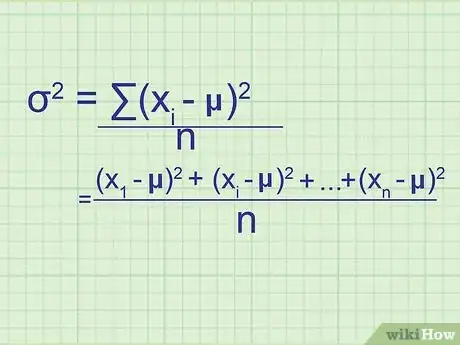





-to-Grams-(g)-Step-12-Version-4.webp)