Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 12 195 volte
A prima vista, i logaritmi potrebbero sembrare difficili da usare, ma sono esattamente come le potenze o i polinomi: devi solo imparare i procedimenti corretti. Hai bisogno solamente di un paio di proprietà elementari per dividere due logaritmi con la stessa base oppure espandere quello che contiene una frazione.
Passaggi
Dividere i Logaritmi a Mano
-
1Osserva il problema alla ricerca di numeri negativi o 1. Il metodo descritto in questa sezione permette di risolvere le divisioni in questa forma: ; tuttavia, non è applicabile per alcuni casi specifici:[1]
- Il logaritmo di un numero negativo è indefinito per tutte le basi (ad esempio o ); in questo caso, scrivi "nessuna soluzione".
- Il logaritmo di 0 è indefinito per tutte le basi; se trovi un termine come , scrivi "nessuna soluzione".
- Il logaritmo di 1 in qualsiasi base () è sempre pari a zero, dato che per ogni x; sostituisci il logaritmo con il numero 0 invece di usare il metodo descritto qui di seguito.
- Se due logaritmi hanno una base differente, come e non puoi semplificare uno dei due come numero intero, il problema non è risolvibile a mano.
-
2Converti l'espressione in logaritmo. Supponendo che il problema non rientri in uno dei casi sopra descritti, puoi semplificarlo in un solo logaritmo; per farlo, usa la formula .
- Primo esempio: risolvi il problema .
Per prima cosa, converti la frazione in un logaritmo usando la formula descritta in precedenza: . - Questa è la formula di "cambio di base" che deriva dalle proprietà elementari dei logaritmi.
- Primo esempio: risolvi il problema .
-
3Calcola la soluzione a mano se possibile. Ricorda che per risolvere devi pensare "", cioè "per quale potenza devo elevare a per ottenere x?". Questo processo non è sempre fattibile senza l'ausilio di una calcolatrice, ma se sei fortunato, potresti imbatterti in un logaritmo semplice.
- Primo esempio: riscrivi come ; il valore di "?" è la soluzione del problema. Puoi trovarlo procedendo per tentativi:
16 è il risultato che stavi cercando, quindi la soluzione di è 4.
- Primo esempio: riscrivi come ; il valore di "?" è la soluzione del problema. Puoi trovarlo procedendo per tentativi:
-
4Lascia la risposta in forma logaritmica se non puoi semplificarla. Alcuni logaritmi sono davvero molto complessi da risolvere a mano; se hai bisogno di trovare un numero per scopi pratici, dovresti usare una calcolatrice. Se stai risolvendo un problema scolastico, è probabile che il docente si aspetti che tu lasci la soluzione in forma di logaritmo. Ecco un altro esempio più complesso che si avvale di questo metodo.
- Secondo esempio: trova la soluzione di .
- Trasforma la frazione in un unico logaritmo: . Nota che 3 di ogni logaritmo iniziale sparisce e questo accade per qualsiasi base.
- Riscrivilo sotto forma di e cerca le possibili soluzioni per "?":
Dato che 58 ricade fra due potenze consecutive, la soluzione di non è un numero intero. - Lascia come soluzione.
Pubblicità
Logaritmi con Frazione
-
1Inizia dalla divisione che si trova all'interno del logaritmo. Questa sezione dell'articolo ti insegna a risolvere i problemi che includono le espressioni nella seguente forma: .
- Per esempio, considera:
"Risolvi per "n" se ".
- Per esempio, considera:
-
2Controlla la presenza di numeri negativi. Il logaritmo di un numero minore di zero è indefinito; se "x" o "y" sono negativi, accertati che il problema possa essere risolto prima di continuare:
- Se "x" o "y" è negativo, non c'è soluzione;
- Se "x" e "y" sono entrambi negativi, togli il segno "-" usando la proprietà ;
- Non ci sono logaritmi di numeri negativi, puoi quindi procedere con la fase successiva.
-
3Espandi il quoziente in due logaritmi. Una proprietà utile è descritta dalla formula: . In altri termini, il logaritmo di una frazione è uguale al logaritmo del numeratore meno quello del denominatore.[2]
- Usa questa proprietà per espandere i termini a sinistra del segno di uguaglianza:
. - Riporta quanto ottenuto nell'equazione originale:
→
.
- Usa questa proprietà per espandere i termini a sinistra del segno di uguaglianza:
-
4Semplifica il logaritmo se possibile. Se qualsiasi nuovo logaritmo dell'espressione ha un numero intero come soluzione, puoi semplificarlo in questa fase.
- L'esempio considerato finora ha un nuovo termine: . Poiché 33 = 27, devi semplificare in 3.
- L'equazione completa ora appare come:
.
-
5Isola la variabile. Proprio come in tutti i problemi di algebra, vale la pena isolare il termine che contiene la variabile in un lato dell'equazione; combina i termini come possibile per semplificare il problema.
-
.
-
-
6Sfrutta altre proprietà dei logaritmi quando necessario. Per isolare la variabile dal resto dell'equazione riscrivi i termini utilizzando diverse proprietà degli stessi.
- Nell'esempio considerato in precedenza, n è ancora "intrappolato" dentro il termine .
Per poter isolare la variabile, usa la proprietà del prodotto fra logaritmi:
. - Inserisci quanto trovato nell'equazione completa:
.
- Nell'esempio considerato in precedenza, n è ancora "intrappolato" dentro il termine .
-
7Continua la semplificazione finché non trovi la soluzione. Ripeti più volte le medesime tecniche algebriche e logaritmiche finché non giungi al risultato. Se non è un numero intero, usa una calcolatrice e arrotonda la soluzione al decimale più significativo.
-
Poiché 39 = 19683, n = 19683.
Pubblicità -












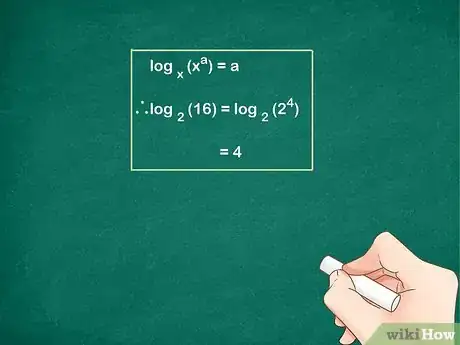



















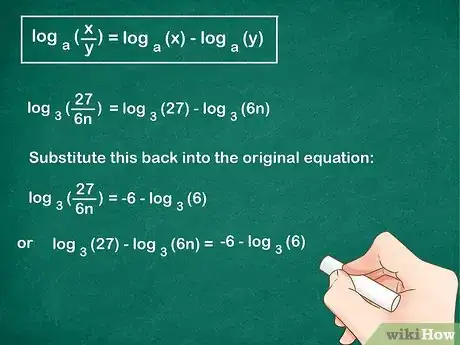



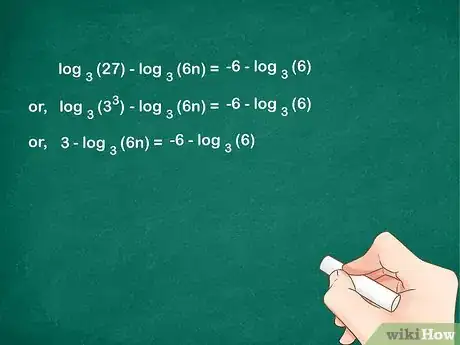


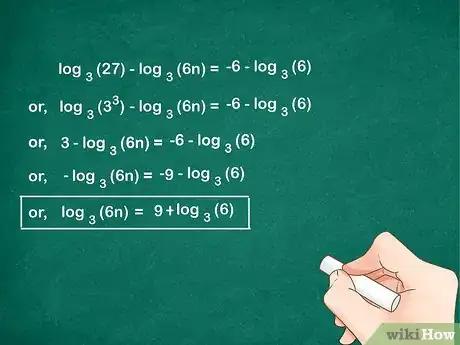


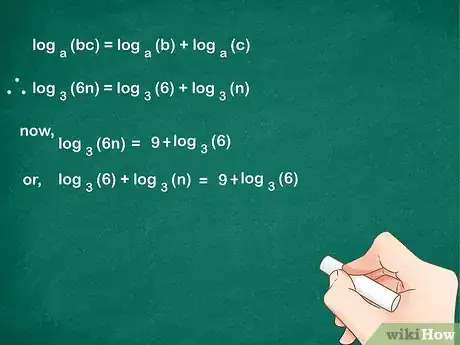




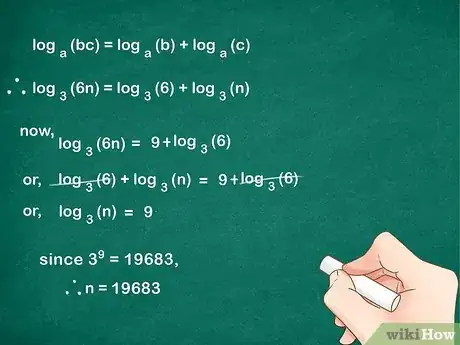




-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 12 195 volte