Questo articolo è stato co-redatto da Courtney Copriviza. Courtney Copriviza è un'insegnante di scuola elementare che vive a Maui, Hawaii. È specializzata in educazione primaria, gestione della classe, sviluppo sociale ed emotivo. Si è laureata in Comunicazione (seguendo al tempo stesso corsi di Educazione Urbana) e in Insegnamento alla Santa Clara University. Ha anche insegnato al liceo a Madrid. È membro della Kappa Delta Pi International Honor Society in Education.
Questo articolo è stato visualizzato 42 647 volte
I bambini hanno spesso difficoltà a comprendere il concetto formale di sottrazione. Quando insegni agli studenti come si eseguono queste operazioni, vale la pena presentarle in varie maniere. Dopo aver spiegato i principi base, affronta il concetto di notazione posizionale e le sottrazioni fra numeri a due cifre. Se ti accorgi che i tuoi ragazzi hanno difficoltà a comprendere questi fondamentali della matematica, fornisci loro diversi metodi e tecniche per risolvere i problemi, ad esempio un approccio alle sottrazioni partendo dalle addizioni oppure con il metodo statunitense del "Common Core" (base comune).
Passaggi
Insegnare le Sottrazioni per Mezzo di Disegni oppure Oggetti Reali
-
1Presenta agli studenti un problema di sottrazioni in forma descrittiva. Scrivilo oppure formulalo ad alta voce:
- Sul tavolo ci sono 8 arance. Giovanni ne mangia 3. Quante arance restano sul tavolo?[1]
-
2Spiega il problema con dei disegni. Traccia otto arance sulla lavagna o su un foglio di carta. Chiedi agli alunni di contarle; etichetta ogni disegno con il numero corrispondente. A questo punto ricorda ai ragazzi che Giovanni ha mangiato 3 frutti, quindi cancellane tre oppure barrali con una X. Infine chiedi agli alunni quante arance sono rimaste.[2]
-
3Spiega il problema con degli oggetti. Metti fisicamente 8 arance sulla cattedra e chiedi agli alunni di contarle. Togline 3 ricordando che si tratta di quelle che Giovanni ha mangiato. A questo punto chiedi ai ragazzi di contare il numero di frutti che rimangono sulla cattedra.[3]
- Quando usi gli oggetti, passa a elementi id uso comune in maniera che gli alunni possano imparare che le regole matematiche sono universali. Per esempio, risolvi il problema usando le arance, quindi proponilo di nuovo impiegando le matite colorate.
-
4Scrivi il problema sotto forma di numeri. Ora puoi spiegare agli alunni che rappresenterai il problema descrittivo con una serie di numeri. Accompagnali durante il processo di "traduzione" dal linguaggio comune a quello matematico.
- Per prima cosa chiedi loro quante arance ci sono sulla scrivania. Scrivi il numero "8" sulla lavagna.
- Ora chiedi ai ragazzi quanti frutti ha mangiato Giovanni. Scrivi "3" sulla lavagna.
- A questo punto chiedi loro se si tratta di un problema di addizione o sottrazione e traccia il segno meno "-" fra "8" e "3".
- Infine, chiedi agli studenti quale sia la soluzione per "8-3". Traccia il simbolo di uguaglianza "=" seguito dal numero "5".[4]
Pubblicità
Insegnare le Sottrazioni Contando a Ritroso sulla Linea dei Numeri
-
1Presenta agli studenti una sottrazione in forma di problema descrittivo. Scrivilo o enuncialo ad alta voce:
- Ci sono 10 cani nel negozio di animali. 6 sono stati adottati da nuovi padroni. Quanti cani restano al negozio?[5]
-
2Usa la linea dei numeri per risolvere il problema. Tracciala sulla lavagna in modo che comprenda i numeri da 0 a 10. A questo punto chiedi agli studenti quanti cani ci sono nel negozio. Appoggia il pennarello o il puntatore sul numero "10". Ora puoi chiedere ai ragazzi quanti cuccioli sono stati adottati. Conta a ritroso 6 spazi partendo dal "10" (9, 8, 7, 6, 5, 4) fino a raggiungere il numeri "4". Ora chiedi nuovamente ai ragazzi quanti cani sono rimasti nel negozio di animali.[6]
- Sarebbe un'ottima idea creare una linea di numeri permanente a cui gli alunni possano fare riferimento. Puoi usare un pennarello su un foglio, un poster, sulla lavagna o un washi colorato sulla lavagna o sul muro.
-
3Riscrivi il problema nel linguaggio matematico. Spiega agli alunni che il problema può essere riscritto usando i numeri. Accompagna i tuoi studenti in questa "traduzione" dal linguaggio comune a quello matematico.
- Chiedi quanti cani ci sono al negozio di animali e scrivi "10" sulla lavagna.
- Ora ricorda loro quanti cuccioli sono stati adottati e traccia il numero "6" sulla lavagna.
- In seguito chiedi agli studenti se si tratta di un problema di sottrazione o addizione e interponi il segno meno "-" fra i valori "10" e "6".
- Domanda quale sia la soluzione della sottrazione "10-6". Scrivi il simbolo di uguaglianza "=" seguito dal numero "4".[7]
Pubblicità
Insegnare le Sottrazioni con le Famiglie di Numeri
-
1Introduci il concetto di famiglie di numeri. Si definisce famiglia di numeri una serie di problemi matematici che utilizzano gli stessi numeri. Ci sono tre numeri in ogni famiglia e questi possono essere sommati o sottratti in modi diversi. Per esempio 10, 3 e 7 formano una famiglia di numeri. Puoi utilizzarli per creare due equazioni di somma e due di sottrazione:
- 10-3=7;
- 10-7=3;
- 7+3=10;
- 3+7=10.[8]
-
2Presenta la sottrazione agli alunni sotto forma di problema descrittivo. Scrivilo oppure enuncialo ad alta voce:
- Ho 7 caramelle e ne mangio 3. Quante caramelle mi restano?[9]
-
3Usa la famiglia di numeri per risolvere il problema. Guida gli alunni passo a passo nel processo:
- Chiedi agli studenti qual è l'operazione matematica che si deve risolvere. Scrivi "7-3=?" sulla lavagna.
- Ora chiedi loro di trovare qual è il terzo numero della famiglia. Per fare ciò scrivi sulla lavagna le seguenti operazioni: "3+__=7"; "__+3=7"; "7-__=3" e "7-3=__". Riempi gli spazi bianchi man mano che gli alunni forniscono le soluzioni.[10]
Pubblicità
Insegnare le Sottrazioni con il Metodo della Base Comune
-
1Spiega il concetto di sottrazione secondo questo metodo. Il metodo della base comune presenta l'idea di sottrazione come misura della distanza fra due punti. Per dimostrarlo e per fornire agli studenti un riferimento visivo, traccia sulla lavagna una linea di numeri che va da 0 a 10.
- Presenta loro una semplice sottrazione: 9-4=?.
- Individua il numero 4 sulla linea dei numeri. Questo è il punto di partenza.
- Ora individua il numero 9 sulla linea dei numeri. Si tratta della destinazione finale.
- Misura o conta la distanza che separa i due punti: "5, 6, 7, 8, 9".
- La distanza è pari a cinque; quindi 9-4=5.[11]
-
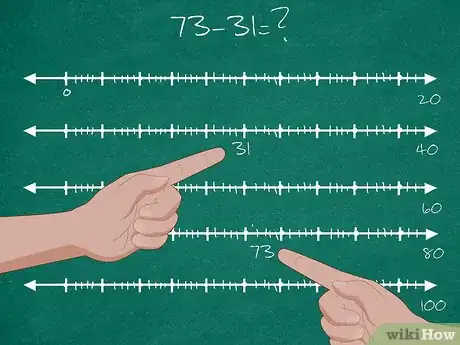
2Risolvi le sottrazioni con numeri a due cifre. In questo caso spiega ai tuoi studenti che ci sono più "tappe intermedie" fra il punto di partenza e quello di arrivo.
- Proponi agli alunni una sottrazione a due cifre: 73-31=?.
- Individua il numero 31 sulla linea dei numeri. Questo rappresenta il punto di partenza.
- Trova il numero 73 sulla stessa linea che rappresenta la destinazione finale.
- "Fermati" al primo valore di cambio delle decine. Spostati da 31 a 40 e annota la soluzione parziale: 9.
- Ora "fermati" al cambio di decina più vicino a 73. Muoviti da 40 a 70 e conta la distanza che li separa annotando la soluzione: 30.
- A questo punto puoi "andare" fino alla destinazione finale. Spostati da 70 a 73 e scrivi il risultato: 3.
- Somma fra loro tutte le misure intermedie: 9+30+3=42. Quindi: 73-31=42.[12]
-
3Risolvi le sottrazioni con numeri a tre cifre. In questo caso devi spiegare agli studenti che oltre a dover fare delle "tappe intermedie", la distanza fra una "fermata" e l'altra sarà maggiore.
- Presenta agli alunni una sottrazione con numero a tre cifre: 815-398=?.
- Trova il numero 398 sulla linea dei numeri perché rappresenta il punto di partenza.
- Individua anche il valore 815, la destinazione finale.
- "Fermati" al primo cambio di decina. Spostati da 398 a 400 e misura la distanza che separa i due numeri. Annota la soluzione: 2.
- A questo punto percorri la linea dei numeri fino a raggiungere il cambio di centinaia più vicino a 815. Vai da 400 a 800 e annota la soluzione: 400.
- "Fermati" di nuovo al cambio di decina più vicino a 815. Spostati da 800 a 810 e misura la distanza fra loro scrivendo il risultato: 10.
- "Giungi" alla destinazione finale. Vai da 810 a 815 e misura la distanza. Scrivi il risultato che è pari a 5.
- Ora non ti resta che procedere alle somme delle varie misure: 2+400+10+5=417. Quindi 815-398=417.[13]
Pubblicità
Consigli
- Permetti allo studente di disegnare degli oggetti se ha difficoltà a risolvere un problema di sottrazione senza la presenza di elementi da manipolare.
Avvertenze
- Prima di continuare con l'insegnamento accertati che gli studenti abbiano compreso appieno i concetti.
Cose che ti Serviranno
- Oggetti da manipolare
- Carta
- Strumenti per scrivere
Riferimenti
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/
- ↑ https://jr.brainpop.com/math/additionandsubtraction/basicsubtraction/

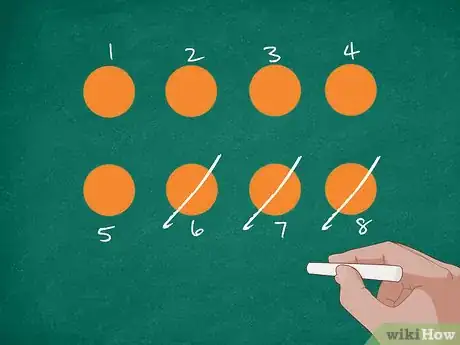
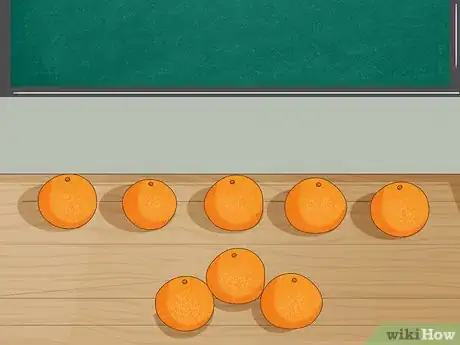
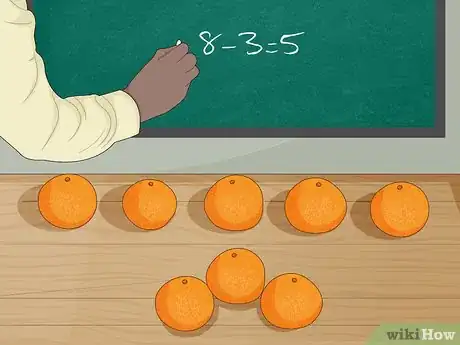

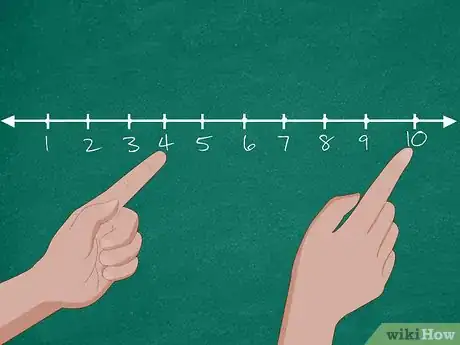




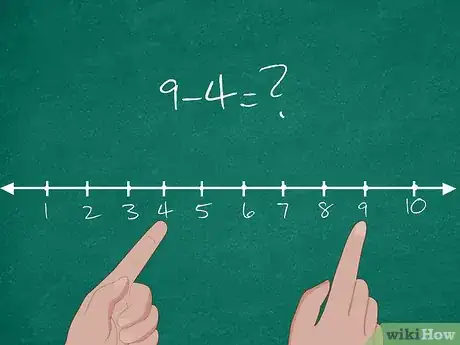




-to-Grams-(g)-Step-12-Version-4.webp)














-to-Grams-(g)-Step-12-Version-4.webp)
