Questo articolo è stato co-redatto da Mario Banuelos, PhD. Mario Banuelos lavora come assistente universitario di matematica alla California State University - Fresno. Con oltre otto anni di esperienza nell'insegnamento, è specializzato in biologia teorica, ottimizzazione, modelli statistici per l'evoluzione del genoma e scienza dei dati. Si è laureato in matematica presso la California State University - Fresno e ha realizzato un dottorato di ricerca in Matematica Applicata alla University of California - Merced. Ha insegnato sia alle scuole superiori sia a livello universitario.
Ci sono 9 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 19 413 volte
Le moltiplicazioni fra frazioni di primo acchito possono sembrare complesse e scoraggianti da affrontare, ma dopo aver compreso come impostare i calcoli e il procedimento da seguire risulteranno semplici e divertenti. Per ottenere il risultato corretto, dovrai trasformare i numeri misti in frazioni improprie, moltiplicare i numeratori, poi i denominatori e infine semplificare la frazione risultante. Prenditi tutto il tempo che ti serve per svolgere i calcoli senza fretta, un passaggio alla volta, in modo da poter tenere sempre sotto controllo il tuo lavoro e individuare rapidamente eventuali errori.
Passaggi
Moltiplicare Frazioni Semplici
-
1Procurati un foglio e una penna per prendere nota del problema da risolvere. Riuscire a visualizzare il lavoro che svolgi ti aiuterà a imparare più velocemente come si eseguono le moltiplicazioni tra frazioni. Questo approccio ti offre anche un altro vantaggio: se dovessi commettere un errore, sarà molto semplice e veloce individuarlo ripercorrendo tutti i passaggi. Tutte le frazioni sono composte da un numeratore (il valore posto nella parte superiore della frazione) e un denominatore (il valore posto sotto al segno di frazione). Il numeratore e il denominatore sono separati da una linea retta orizzontale.[1]
- Cerca di riportare ogni passaggio dei calcoli su una singola riga, così da poter lavorare in modo organizzato ed efficiente.
- Prima di eseguire la moltiplicazione, cerca di semplificare il più possibile tutte le frazioni coinvolte. In questo modo, potrai lavorare con numeri più piccoli e tutto risulterà più facile.
-
2Moltiplica prima i numeratori. Per esempio, se devi risolvere la seguente espressione 5/6 * 2/3, inizia moltiplicando i due numeratori 5 * 2, ottenendo come risultato 10. Quest'ultimo sarà il numeratore della frazione finale.[4]
- Fai pratica risolvendo questo problema di esempio: 3/4 * 1/3. Ricorda che qualsiasi numero moltiplicato per 1 dà come risultato se stesso, quindi in questo caso otterrai 3.
-
3Calcola il denominatore della frazione finale moltiplicando tra loro i denominatori delle frazioni di partenza. Proseguendo con l'esempio precedente, 5/6 * 2/3, dovrai moltiplicare 6 * 3 ottenendo come risultato 18, che corrisponde al denominatore della frazione finale.[5]
- Proseguendo con il secondo esempio, 3/4 * 1/3, dovrai moltiplicare 4 * 3 ottenendo come risultato 12. La frazione finale sarà pari a 3/12.
-
4Semplifica il più possibile il risultato che hai ottenuto. Il numeratore e il denominatore di una frazione condividono dei fattori comuni (cioè tutti quei numeri in grado di dividere il numeratore e il denominatore, ottenendo come risultato dei valori interi) che puoi usare per semplificare il risultato ottenuto. Per esempio, il risultato della seguente espressione 5/6 * 2/3 è pari a 10/18. In questo caso, sia 10 sia 18 sono divisibili per 2. Dividendo il numeratore e il denominatore della frazione in esame per 2, otterrai il risultato finale del tuo lavoro, cioè 5/9.[6]
- Semplifica la frazione 3/12. Dato che il numeratore e il denominatore possono essere interamente divisi per 3, il risultato finale della semplificazione sarà 1/4.
Pubblicità
Lavorare con i Numeri Misti
-
1Prendi nota del problema di partenza usando un foglio di carta in modo da poter tenere sempre sotto controllo il tuo lavoro. Potresti essere tentato di svolgere tutti i calcoli direttamente a mente, ma all'inizio è sempre meglio usare carta e penna, eseguendo un passaggio alla volta. Utilizzando questo metodo, se dovessi commettere un errore sarà molto semplice e rapido individuarlo, esaminando passaggio dopo passaggio tutto il tuo lavoro.
- Tutte le frazioni sono composte da due parti: un numeratore (il valore posto nella parte superiore della frazione) e un denominatore (il valore posto sotto al segno di frazione). Il numeratore e il denominatore sono separati da una linea retta orizzontale. Un numero misto è composto da una parte intera seguita da una frazionaria.
-
2Converti il numero misto in una frazione impropria. Per esempio, ipotizza di dover risolvere la seguente espressione algebrica (1 + 3/4) * (7 + 1/5). Il primo passo consiste nel trasformare i due numeri misti in due frazioni improprie. Una frazione si definisce impropria quando il numeratore è maggiore del denominatore. Segui queste istruzioni per eseguire la conversione:[7]
- Il numero misto (1 + 3/4) è equivalente alla frazione impropria 7/4. Il denominatore della parte frazionaria di un numero misto è sempre uguale a quello della frazione impropria risultante dalla conversione. Per ottenere il numeratore, occorre moltiplicare il denominatore per la parte intera (4 *1) e sommarlo al numeratore della parte frazionaria (3). In questo esempio, otterrai (4*1) + 3 = 7.
- Se devi convertire in una frazione impropria il seguente numero misto (7 + 1/5), moltiplica il denominatore della parte frazionaria per la parte intera (5*7), quindi somma il prodotto ottenuto al numeratore della parte frazionaria (1). In questo caso, otterrai (5*7) + 1 = 36. A questo punto, completa la conversione riportando il risultato ottenuto al numeratore della frazione impropria e conservando al denominatore quello della parte frazionaria del numero misto iniziale. Il numero misto (7 + 1/5) è equivalente alla frazione impropria 36/5.
-
3Semplifica le frazioni improprie per ottenere numeri più piccoli e più semplici da moltiplicare fra loro. Proseguendo con l'esempio precedente, devi eseguire il seguente calcolo: 7/4 * 36/5. Anche se potresti procedere subito alla moltiplicazione dei numeratori e dei denominatori delle due frazioni, i calcoli risulteranno molto più semplici semplificando prima le frazioni improprie. Puoi eseguire una semplificazione incrociata verificando se il numeratore di una frazione e il denominatore dell'altra possono essere divisi interamente per il medesimo numero. Nell'esempio in oggetto, 7 e 5 non hanno un fattore in comune, ma 36 e 4 possono essere divisi per 4. Segui queste istruzioni per semplificare le frazioni di esempio:[8]
- Dividi 4 per se stesso ottenendo come risultato 1, quindi la prima frazione impropria, 7/4, diventa 7/1;
- Dividi 36 per 4 ottenendo come risultato 9, quindi la seconda frazione impropria, 36/5, diventa 9/5;
- A questo punto, puoi anche semplificare le singole frazioni, se i rispettivi numeratori e denominatori hanno un fattore in comune. Per esempio, se invece di 7/4 avessi ottenuto 8/4, avresti potuto semplificare la frazione nella seguente forma 2/1.
-
4Esegui i calcoli moltiplicando i numeratori e i denominatori delle due frazioni. A questo punto, devi completare il tuo lavoro moltiplicando 7 per 9 ottenendo 63, che corrisponde al numeratore della frazione finale. Adesso, moltiplica 1 per 5 ottenendo come risultato 5 che corrisponde al denominatore della frazione finale. La frazione impropria che equivale al risultato del tuo problema di partenza è 63/5.[9]
Consiglio: ricorda di tenere traccia di ogni singolo passaggio dei calcoli, così da poter lavorare in modo organizzato ed efficiente. Potrebbe risultare un po' difficile gestire i numeri misti e le frazioni improprie, ma con la pratica diventerà tutto più semplice e intuitivo.
-
5Converti la frazione impropria finale in un numero misto per ottenere la soluzione al problema di partenza. Per convertire una frazione impropria in un numero misto, esegui semplicemente una divisione. Dividi il numeratore della frazione per il denominatore. Nell'esempio precedente dovrai eseguire il seguente calcolo 63/5 ottenendo come risultato 12 con il resto di 3. Il quoziente della divisione, 12, corrisponde alla parte intera del numero misto, mentre il resto, 3, diventerà il numeratore della parte frazionaria. Il denominatore invece rimane quello originale di partenza, che in questo caso è 5. Al termine di tutto il processo di calcolo, hai ottenuto che (1 + 3/4) * (7 + 1/5) = 12 + 3/5.[10]
- Se non riesci a eseguire le divisioni fra interi a mente, aiutati con un foglio di carta e una penna.
Pubblicità
Usare la Calcolatrice
-
1Trasforma una frazione in un numero decimale per eseguire i calcoli utilizzando una calcolatrice. Inserisci ogni frazione nella calcolatrice singolarmente per convertirle nei numeri decimali equivalenti. Per esempio, se devi risolvere la seguente espressione algebrica 3/4 * 1/2, inizia convertendo la prima frazione, 3/4, digitando il tasto 3, premendo il tasto dell'operazione di divisione e il tasto 4. Otterrai come risultato 0,75. Converti la seconda frazione, 1/2, premendo il tasto 1, premendo il tasto di divisione e infine digitando il numero 2. Otterrai come risultato 0,5.[9]
- Alcune calcolatrici offrono la possibilità di inserire i numeri frazionari direttamente nella loro forma originale di frazione. In tal caso non dovrai lavorare con i numeri decimali. Controlla il manuale di istruzioni della tua calcolatrice per verificare se offre questa possibilità.
-
2Se devi lavorare coi numeri misti, dovrai semplicemente sommare la parte intera al numero decimale. In altre parole, dovrai sostituire il valore 0 della parte intera del numero decimale con il valore che corrisponde alla parte intera del numero misto. È molto semplice lavorare con i numeri misti, anche se la tua calcolatrice non permette di gestire le frazioni nella loro forma originale. Segui queste istruzioni per trasformare la parte frazionaria di un numero misto in un valore decimale, aggiungere la parte intera prima del separatore decimale e continuare nella risoluzione del problema iniziale.[10]
- Per esempio, per convertire il numero misto 3 + 3/4 in un decimale, dovrai dividere 3 per 4 usando la calcolatrice ottenendo 0,75, quindi riportare il numero 3 sul lato sinistro del separatore decimale ottenendo 3,75.
-
3Moltiplica i numeri decimali usando la calcolatrice. Per esempio, se devi moltiplicare 3/4 per 1/2, digita 0,75 * 0,5 usando la tastiera della calcolatrice. Il risultato che otterrai sarà 0,375. Può essere di aiuto tenere traccia su un foglio di carta dei singoli passaggi e dei singoli risultati parziali, nel caso dovessi commettere un errore o premere il tasto sbagliato della calcolatrice.[11]
- Se stai usando una calcolatrice scientifica che ti permette di utilizzare le parentesi, allora sarai in grado di inserire direttamente l'intera espressione da risolvere nella sua forma originale. In questo caso, dovrai semplicemente digitare la seguente sequenza: (3/4) * (1/2). Il simbolo "/" indica che dovrai premere il tasto relativo all'operazione di divisione.
-
4Converti il valore decimale in una frazione. Su un foglio di carta, riporta il numero decimale al numeratore di una frazione con denominatore pari a 1. Proseguendo con l'esempio precedente, 3/4 * 1/2, dovrai scrivere sul foglio la seguente frazione 0,375/1. Moltiplica il numeratore e il denominatore per il multiplo di 10 corrispondente al numero di cifre decimali del valore da convertire. Nell'esempio in oggetto, il valore 0,375 ha 3 cifre decimali, quindi dovrai moltiplicare numeratore e denominatore della frazione per 1000 (se necessario, usa la calcolatrice per eseguire i calcoli). Alla fine di questo passaggio, dovresti aver ottenuto il seguente risultato 375/1000.[12]
- Se stai usando una calcolatrice scientifica che permette di inserire i valori direttamente sotto forma di frazione, dovresti essere in grado di convertire un numero decimale in frazione utilizzando direttamente la funzione del dispositivo.
-
5Semplifica la frazione ottenuta per ricavare il risultato finale. Dopo aver convertito il numero decimale in una frazione, dovrai semplificarla per completare il lavoro. Nel caso di numeri grandi potresti avere la necessità di eseguire la semplificazione più volte, per ottenere la frazione più piccola possibile. Per esempio, nel caso della seguente frazione 375/1000, sia il numeratore sia il denominatore sono divisibili per 5, quindi eseguendo i calcoli otterrai 75/200. Anche la frazione risultante dalla prima semplificazione può essere nuovamente ridotta per 5, ottenendo 15/40. Eseguendo un'ulteriore semplificazione, otterrai il risultato finale, cioè 3/8.[13]
- Se per arrivare al risultato finale devi eseguire più semplificazioni in successione non ti preoccupare si tratta di una cosa del tutto normale. Prenditi tutto il tempo che ti serve, non avere fretta di completare il lavoro e raggiungerai il tuo obiettivo senza errori e senza sforzo.
Pubblicità
Consigli
- Se devi risolvere un'espressione algebrica che include moltiplicazioni e addizioni o sottrazioni tra frazioni, ricorda di rispettare sempre l'ordine degli operatori matematici. Prima di eseguire una somma o una sottrazione devi sempre eseguire la moltiplicazione. Per esempio, se devi risolvere la seguente espressione 7/13 + 5/8 * 8/9, dovrai prima eseguire la moltiplicazione, 5/8 * 8/9, per poi sommare il prodotto ottenuto alla frazione 7/13.
Riferimenti
- ↑ www.youtu.be/CTKMK1ZGLuk?t=12
- ↑ www.youtu.be/CTKMK1ZGLuk?t=12
- ↑ www.youtu.be/CTKMK1ZGLuk?t=42
- ↑ www.youtu.be/CTKMK1ZGLuk?t=61
- ↑ www.youtu.be/RPhaidW0dmY?t=15
- ↑ www.youtu.be/RPhaidW0dmY?t=126
- ↑ www.youtu.be/RPhaidW0dmY?t=154
- ↑ www.youtu.be/RPhaidW0dmY?t=173
- ↑ https://sciencing.com/make-fraction-scientific-calculator-5843488.html
Informazioni su questo wikiHow
Per moltiplicare le frazioni, inizia moltiplicando tra loro i numeratori, che sono i numeri sopra la linea. Per esempio, se stai cercando di risolvere 2/3 × 3/4, dovrai moltiplicare 2 per 3 e ottenere 6. Dopodiché, moltiplica tra loro i denominatori, che sono i numeri al di sotto della linea. In questo esempio, moltiplicheresti 3 per 4 e otterresti 12. Pertanto, la tua nuova frazione sarebbe 6/12. Una volta ottenuta la tua nuova frazione, riducila ai minimi termini. Per semplificare la frazione, basta dividere il numeratore e il denominatore per il numero più grande che è contenuto da entrambi i numeri, noto anche come massimo comun divisore. In questo caso, dal momento che 6 è il numero più grande che può essere contenuto nel numero in alto e in quello in basso, dovrai dividere 6 per 6 e 12 per 6, ottenendo 1/2. Continua a leggere l'articolo se vuoi imparare a semplificare le frazioni prima di moltiplicarle!
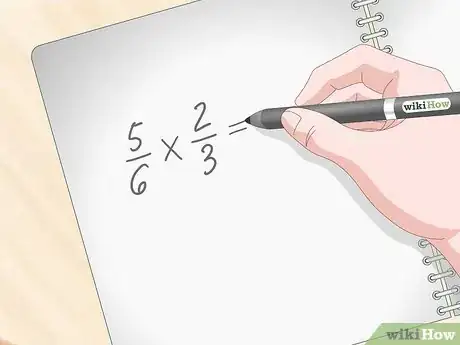
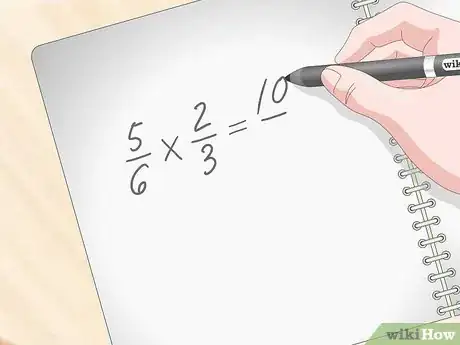
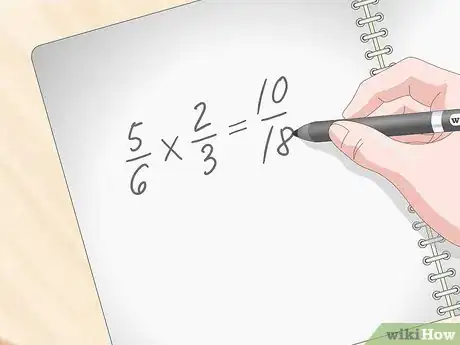
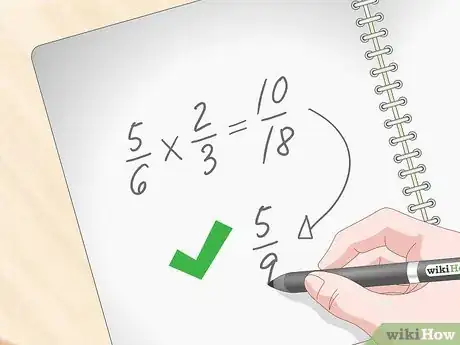
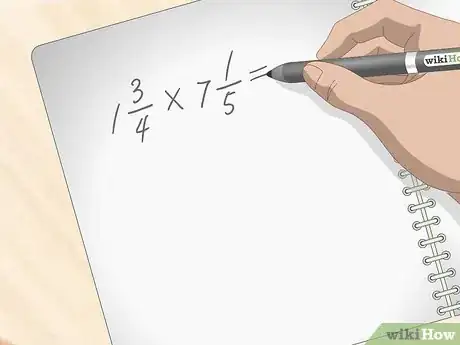

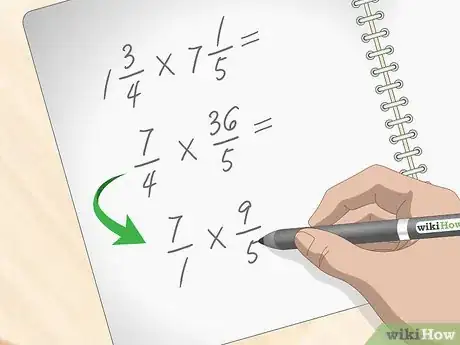
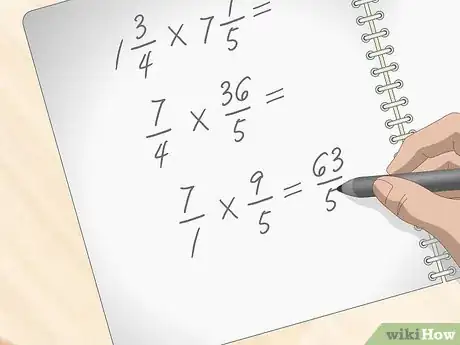
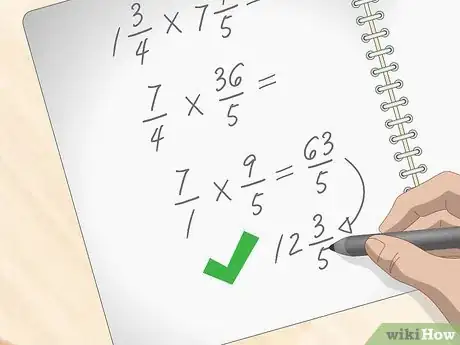



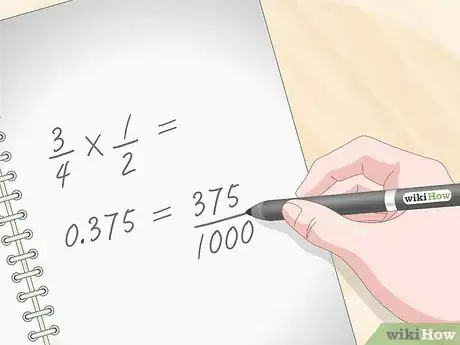
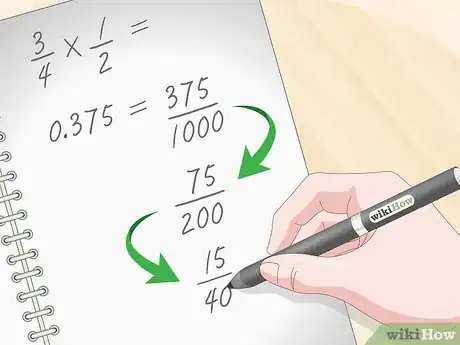



-to-Grams-(g)-Step-12-Version-4.webp)














-to-Grams-(g)-Step-12-Version-4.webp)
