Come Normalizzare un Vettore

Info sull'Autore

Un vettore è un oggetto geometrico che ha una direzione e una magnitudine. Viene rappresentato come un segmento orientato dotato di punto iniziale e una freccia sull'estremità opposta; la lunghezza del segmento è proporzionale alla magnitudine e la direzione della freccia indica il verso. La normalizzazione di un vettore è un esercizio piuttosto comune in matematica e ha diverse applicazioni pratiche nella computer grafica.

Metodo 1

Metodo 1 di 5:

Definire i Termini

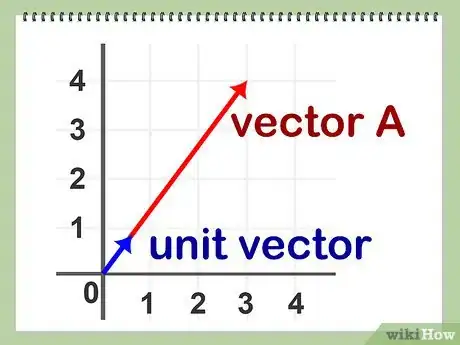
1
Definisci il vettore unitario o versore. Il versore del vettore A è appunto un vettore che possiede il medesimo verso e direzione di A, ma lunghezza pari a 1 unità; si può dimostrare matematicamente che per ciascun vettore A esiste un solo vettore unitario.
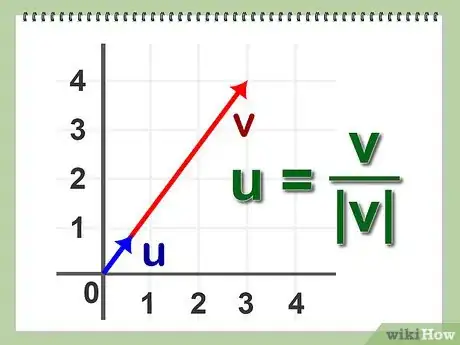
2
Definisci la normalizzazione di un vettore. Si tratta di identificare il vettore unitario per quello A dato.
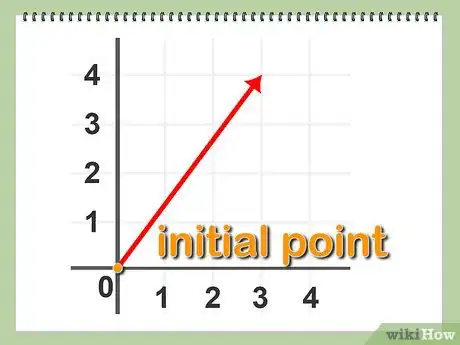
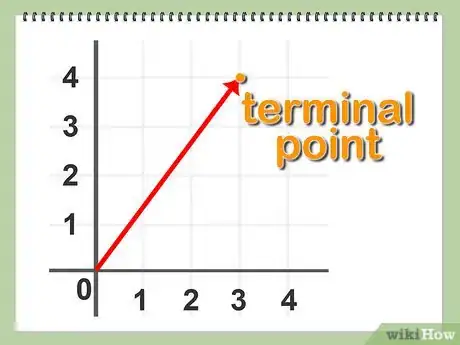
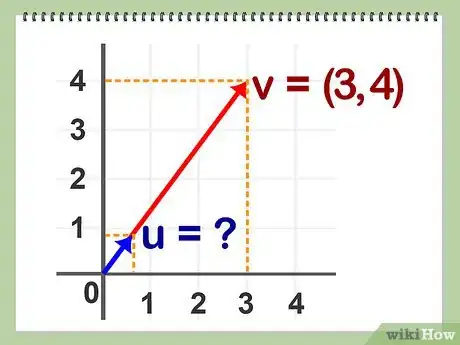
3
Definisci il vettore applicato. Si tratta di un vettore il cui punto iniziale coincide con l'origine del sistema di coordinate all'interno di uno spazio cartesiano; tale origine si definisce con la coppia di coordinate (0,0) in un sistema bidimensionale. In questo modo, puoi identificare il vettore facendo riferimento solamente al punto terminale.
4
Descrivi la notazione vettoriale. Limitandoti ai vettori applicati, puoi indicare il vettore come A = (x,y), dove la coppia di coordinate (x,y) definisce il punto terminale del vettore stesso.

Pubblicità

Metodo 2

Metodo 2 di 5:

Analizzare l'Obiettivo

1
Stabilisci i valori noti. Dalla definizione di versore puoi dedurre che il punto iniziale e la direzione coincidono con quelli del dato vettore A; inoltre, sai per certo che la lunghezza del versore è pari a 1.
2
Determina il valore ignoto. L'unica variabile che devi calcolare è il punto finale del vettore.

Pubblicità

Metodo 3

Metodo 3 di 5:

Derivare la Soluzione per il Vettore Unitario

Trova il punto finale del versore del vettore A = (x, y). Grazie alla proporzionalità tra triangoli simili, sai che ogni vettore che ha la medesima direzione di A possiede come terminale il punto con coordinate (x/c,y/c) per ogni valore di "c"; inoltre, sai che la lunghezza del versore è pari a 1. Di conseguenza, sfruttando il teorema di Pitagora: [x^2/c^2 + y^2/c^2]^(1/2) = 1 -> [(x^2 + y^2)/c^2]^(1/2) -> (x^2 + y^2)^(1/2)/c = 1 -> c = (x^2 + y^2)^(1/2); ne consegue che il versore u del vettore A = (x, y) viene definito come u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2))

Metodo 4

Metodo 4 di 5:

Normalizzare un Vettore in uno Spazio Bidimensionale

Considera il vettore A il cui punto iniziale coincide con l'origine e quello finale con le coordinate (2,3), di conseguenza A = (2,3). Calcola il versore u = (x/(x^2 + y^2)^(1/2), y/(x^2 + y^2)^(1/2)) = (2/(2^2 + 3^2)^(1/2), 3/(2^2 + 3^2)^(1/2)) = (2/(13^(1/2)), 3/(13^(1/2))). Quindi, A = (2,3) si normalizza a u = (2/(13^(1/2)), 3/(13^(1/2))).

Metodo 5

Metodo 5 di 5:

Normalizzare un Vettore in uno Spazio con "n" Dimensioni

Generalizza l'equazione di normalizzazione per uno spazio con un numero qualsiasi di dimensioni. Il vettore A (a, b, c, …) è normalizzato a u = (a/z, b/z, c/z, …) dove z = (a^2 + b^2 + c^2 …)^(1/2).