wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 59 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 45 990 volte
In un "sistema di equazioni" viene richiesto di risolvere due o più equazioni allo stesso tempo. Quando ci sono due variabili differenti, come x e y oppure a e b, potrebbe sembrare un compito difficile, ma solo a prima vista. Per fortuna, una volta appreso il metodo da applicare, tutto ciò che ti servirà saranno delle conoscenze basiche di algebra. Se preferisci apprendere con metodi visivi, o il tuo insegnante richiede anche una rappresentazione grafica delle equazioni, allora devi anche imparare a creare un grafico. I grafici sono utili per "vedere come si comportano le equazioni" e per verificare il lavoro, ma si tratta di un metodo più lento che non si presta molto bene ai sistemi di equazioni.
Passaggi
Per Sostituzione
-
1Sposta le variabili ai lati delle equazioni. Per iniziare questo metodo di "sostituzione", devi prima "risolvere per x" (o per qualunque altra variabile) una delle due equazioni. Ad esempio, nell’equazione: 4x + 2y = 8, riscrivi i termini sottraendo 2y da ciascun lato per ottenere: 4x = 8 - 2y.
- In seguito, questo metodo prevede l’uso di frazioni. Se non ami lavorare con le frazioni, prova il metodo a eliminazione che verrà spiegato successivamente.
-
2Dividi entrambi i lati dell’equazione per "risolverla per x". Una volta che hai spostato la variabile x (o quella che hai scelto) a un lato del segno di uguaglianza, dividi entrambi i termini per isolarla. Ad esempio:
- 4x = 8 - 2y.
- (4x)/4 = (8/4) - (2y/4).
- x = 2 - ½y.
-
3Inserisci questo valore nell’altra equazione. Accertati di considerare, ora, la seconda equazione e non quella sulla quale hai già lavorato. All’interno di questa equazione sostituisci il valore della variabile che hai trovato. Ecco come procedere:
- Sai che x = 2 - ½y.
- La seconda equazione, che non hai ancora elaborato è: 5x + 3y = 9.
- In questa seconda equazione sostituisci la variabile x con "2 - ½y" e ottieni 5(2 - ½y) + 3y = 9.
-
4Risolvi l’equazione che presenta una sola variabile. Usa le classiche tecniche algebriche per trovarne il valore. Se con questo procedimento la variabile si elimina, vai al passaggio successivo. Altrimenti trova la soluzione per una delle equazioni:
- 5(2 - ½y) + 3y = 9.
- 10 – (5/2)y + 3y = 9.
- 10 – (5/2)y + (6/2)y = 9 (Se non hai compreso questo passaggio, leggi come sommare delle frazioni fra loro. Si tratta di un calcolo che si presenta spesso, anche se non sempre, in questo metodo).
- 10 + ½y = 9.
- ½y = -1.
- y = -2.
-
5Utilizza la soluzione che hai trovato per ricavare il valore della prima variabile. Non fare l’errore di lasciare il problema per metà irrisolto. Ora devi inserire il valore della seconda variabile all’interno della prima equazione, così da trovare la soluzione per x:
- Sai che y = -2.
- Una delle equazioni originali è 4x + 2y = 8 (Per questo passaggio puoi usare una qualunque delle equazioni).
- Inserisci -2 al posto di y: 4x + 2(-2) = 8.
- 4x - 4 = 8.
- 4x = 12.
- x = 3.
-
6Ora vediamo cosa fare nel caso entrambe le variabili si elidano. Quando inserisci x=3y+2 o un valore analogo in un’altra equazione, stai cercando di ridurre una equazione con due variabili a una equazione con una variabile. Tuttavia, a volte, capita che le variabili si elidano e che tu ottenga un’equazione senza variabili. Controlla due volte i tuoi calcoli per essere certo di non avere commesso errori. Se sei certo di avere eseguito tutto correttamente, dovresti ottenere uno dei seguenti risultati:
- Se ottieni un'equazione senza variabili che non è vera (ad esempio 3=5) allora il sistema non ha soluzione. Se tracci il grafico delle equazioni troverai che si tratta di due rette parallele che mai si intersecheranno.
- Se ottieni un'equazione senza variabili che è vera (come 3=3) allora il sistema ha infinite soluzioni. Le sue equazioni sono esattamente identiche fra loro e se ne tracci la rappresentazione grafica ottieni la stessa linea.
Pubblicità
A Eliminazione
-
1Trova la variabile da cancellare. A volte, le equazioni sono scritte in maniera tale che una variabile si può "già eliminare". Ad esempio quando il sistema è composto da: 3x + 2y = 11 e 5x - 2y = 13. In tal caso "+2y" e "-2y" si elidono fra loro e si può togliere la variabile "y" dal sistema. Analizza le equazioni e trova una delle variabile che è possibile cancellare. Se ti rendi conto che non è possibile, vai al prossimo passaggio.
-
2Moltiplica una equazione per cancellare una variabile. Salta questo passaggio se hai già eliso una variabile. Se non ci sono variabili eliminabili in modo naturale, devi manipolare le equazioni. Questo processo si spiega meglio con un esempio:
- Supponiamo che hai un sistema di equazioni: 3x - y = 3 e -x + 2y = 4.
- Cambiamo la prima equazione in modo da poter cancellare la y. Potresti farlo anche con la x ottenendo sempre lo stesso risultato.
- La variabile - y della prima equazione deve essere eliminata con + 2y della seconda. Per far sì che questo accada, moltiplica - y per 2.
- Moltiplica entrambi i termini della prima equazione per 2 e ottieni: 2(3x - y)=2(3) quindi 6x - 2y = 6. Ora puoi eliminare - 2y con +2y della seconda equazione.
-
3Combina le due equazioni. Per farlo somma fra loro i termini a destra di entrambe le equazioni e fai lo stesso per i termini a sinistra. Se hai modificato correttamente le equazioni, le variabili dovrebbero cancellarsi. Ecco un esempio:
- Le tue equazioni sono 6x - 2y = 6 e -x + 2y = 4.
- Somma fra loro i lati a sinistra: 6x - 2y - x + 2y = ?
- Somma fra loro i lati a destra: 6x - 2y - x + 2y = 6 + 4.
-
4Risolvi l’equazione per la variabile rimasta. Semplifica l’equazione combinata utilizzando le tecniche basilari di algebra. Se non ci sono variabili dopo la semplificazione, vai all’ultimo passaggio di questa sezione. Altrimenti completa i calcoli per trovare il valore di una variabile:
- Hai l’equazione 6x - 2y - x + 2y = 6 + 4.
- Raggruppa le incognite x e y: 6x - x - 2y + 2y = 6 + 4.
- Semplifica: 5x = 10.
- Risolvi per x: (5x)/5 = 10/5 quindi x = 2.
-
5Trova il valore dell’altra incognita. Ora conosci una delle due variabili ma non la seconda. Inserisci il valore che hai trovato in una delle equazioni originali e svolgi i calcoli:
- Ora sai che x = 2 e una delle equazioni originali è 3x - y = 3.
- Sostituisci la x con 2: 3(2) - y = 3.
- Risolvi per y: 6 - y = 3.
- 6 - y + y = 3 + y perciò 6 = 3 + y.
- 3 = y.
-
6Consideriamo il caso che entrambe le incognite si elidano. A volte, combinando fra loro le equazioni di un sistema, le variabili spariscono, rendendo l’equazione priva di senso e inutile ai tuoi scopi. Controlla sempre i calcoli per essere certo di non avere commesso errori e scrivi una di queste risposte come tua soluzione:
- Se hai combinato le equazioni e ne hai ottenuta una senza incognite e che non è vera (come 2=7) allora il sistema non ha soluzione. Se tracci un grafico otterrai due parallele che non si incrociano mai.
- Se hai combinato le equazioni e ne hai ottenuta una senza incognite e vera (come 0=0) allora ci sono infinite soluzioni. Le due equazioni sono perfettamente identiche e se ne tracci la rappresentazione grafica ottieni la medesima linea.
Pubblicità
Con il Grafico
-
1Usa questo metodo solo se ti viene richiesto. A meno che tu non stia usando un computer o una calcolatrice grafica, sarai in grado di risolvere la maggior parte dei sistemi solo per approssimazione. Il tuo insegnante o il libro di testo ti chiederanno di applicare il metodo grafico solo per farti esercitare nella rappresentazione delle equazioni. Tuttavia puoi usarlo anche per verificare il tuo lavoro dopo aver trovato le soluzioni con gli altri procedimenti.
- Il concetto di base è quello di rappresentare entrambe le equazioni su un grafico e trovare i punti in cui i tracciati si incrociano (le soluzioni). I valori di x e y rappresentano le coordinate del sistema.
-
2Risolvi entrambe le equazioni per y. Mantienile separate ma riscrivile isolando la y a sinistra del segno di uguaglianza (utilizza semplici passaggi algebrici). Alla fine dovresti ottenere le equazioni sotto forma di "y = __x + __". Ecco un esempio:
- La tua prima equazione è 2x + y = 5, cambiala in y = -2x + 5.
- La tua seconda equazione è -3x + 6y = 0, cambiala in 6y = 3x + 0 e semplificala come y = ½x + 0.
- Se ottieni due equazioni identiche la stessa linea sarà un’unica "intersezione" e potrai scrivere che ci sono infinite soluzioni.
-
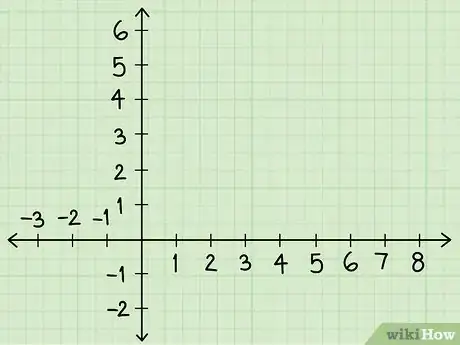
3Disegna gli assi cartesiani. Prendi un foglio di carta millimetrata e disegna l’asse verticale "delle y" (detto delle ordinate) e quello orizzontale "delle x" (detto delle ascisse). Partendo dal punto in cui si intersecano (origine o punto 0;0) scrivi i numeri 1, 2, 3, 4 e così via sull’asse verticale (verso l’alto) e orizzontale (verso destra). Scrivi i numeri -1, -2 sull’asse delle y dall’origine verso il basso e sull’asse delle x dall’origine verso sinistra.
- Se non hai la carta millimetrata, usa un righello e sii preciso nel distanziare i numeri in maniera uniforme.
- Se devi utilizzare dei numeri grandi o i decimali, puoi cambiare la scala del grafico (ad esempio 10, 20, 30 oppure 0,1; 0,2 e così via).
-
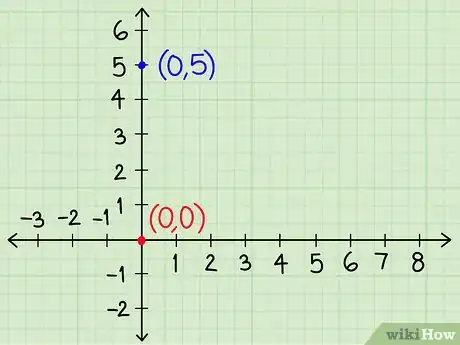
4Traccia l’intercetta per ogni equazione. Ora che hai trascritto queste come y = __x + __, puoi iniziare a disegnare un punto corrispondente all’intercetta. Questo significa porre y uguale all’ultimo numero dell’equazione.
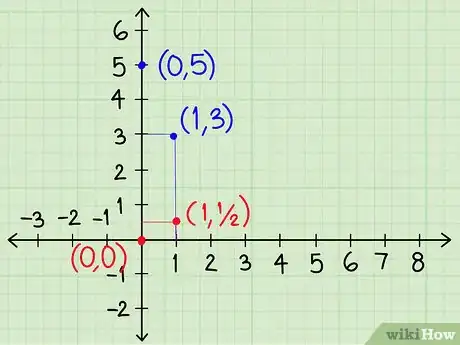
- Nei nostri esempi precedenti, una equazione (y = -2x + 5) interseca l’asse y nel punto 5, l’altra (y = ½x + 0) nel punto 0. Questi corrispondono ai punti di coordinate (0;5) e (0;0) sul nostro grafico.
- Usa penne di colori diversi per tracciare le due linee.
-
5Usa il coefficiente angolare per continuare il tracciato delle rette. Nella forma y = __x + __, il numero davanti all’incognita x è il coefficiente angolare della retta. Ogni volta che il valore di x aumenta di una unità, il valore di y aumenta di tante volte quanto è il coefficiente angolare. Usa questa informazione per trovare il punto di ogni retta per il valore di x=1. In alternativa poni x=1 e risolvi le equazioni per y.
- Manteniamo le equazioni dell’esempio precedente e otteniamo che y = -2x + 5 ha un coefficiente angolare di -2. Quando x=1 la retta si sposta verso il basso di 2 posizioni rispetto al punto occupato per x=0. Traccia il segmento che collega il punto con coordinate (0;5) e (1;3).
- L’equazione y = ½x + 0 ha un coefficiente angolare di ½. Quando x=1 la retta sale di ½ spazio rispetto al punto corrispondente a x=0. Traccia il segmento che unisce i punti di coordinate (0;0) e (1;½).
- Se le rette hanno lo stesso coefficiente angolare sono fra loro parallele e non si intersecheranno mai. Il sistema non ha soluzione.
-
6Continua a trovare i vari punti per ogni equazione finché trovi che le rette si intersecano. Fermati e osserva il grafico. Se le linee si sono già incrociate, segui il passaggio successivo. Altrimenti prendi una decisione in base a come si comportano le rette:
- Se le rette convergono fra loro, continua a trovare i punti in quella direzione.
- Se le rette di allontanano l’una dall’altra, allora torna indietro e partendo dai punti con ascissa x=1 procedi nell’altra direzione.
- Se le linee non sembrano avvicinarsi in nessuna direzione, allora fermati e riprova con punti fra loro più distanti, ad esempio con ascissa x=10.
-
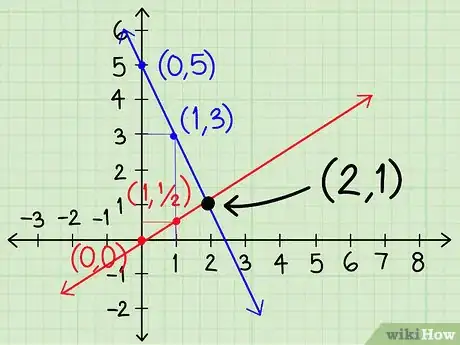
7Trova la soluzione all’intersezione. Quando le linee si incrociano, i valori delle coordinate x e y rappresentano la risposta al tuo problema. Se sei fortunato, saranno anche dei numeri interi. Nel nostro esempio, le rette di intersecano a (2;1) quindi puoi scrivere la soluzione come x = 2 e y = 1. In alcuni sistemi, le linee si intersecheranno in punti compresi fra due numeri interi e, a meno che il tuo grafico sia estremamente preciso, sarà difficile determinare il valore della soluzione. Se ciò dovesse accadere, puoi formulare la tua risposta come "1<x<2" oppure usare il metodo di sostituzione o eliminazione per trovare una soluzione precisa.Pubblicità
Consigli
- Puoi fare una verifica del tuo lavoro, inserendo le soluzioni che hai ottenuto nelle equazioni originali. Se ottieni un’equazione vera (ad esempio 3=3), allora la tua soluzione è corretta.
- Nel metodo a eliminazione, a volte dovrai moltiplicare un’equazione per un numero negativo per poter cancellare una variabile.
Avvertenze
- Questi metodi non funzionano se le incognite sono elevate a potenza, come x2. Per avere più dettagli in merito alla risoluzione di equazioni di questo tipo, cerca una guida per scomporre in fattori i polinomi di secondo grado con due variabili.
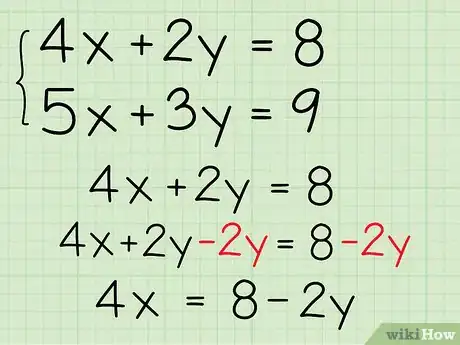

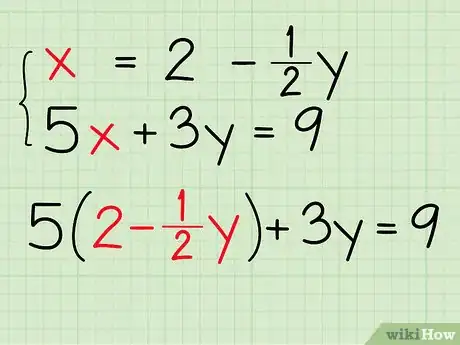

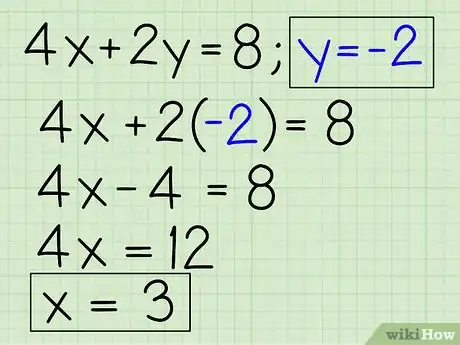
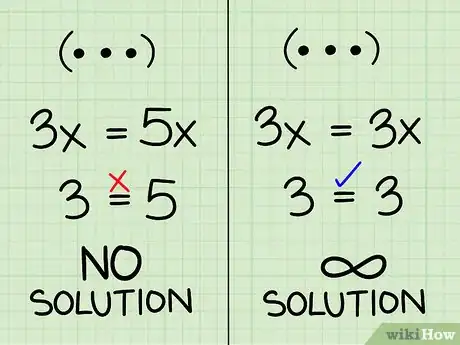
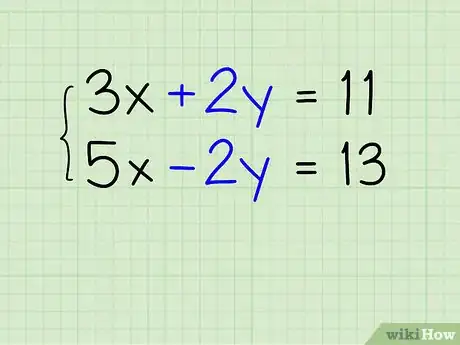

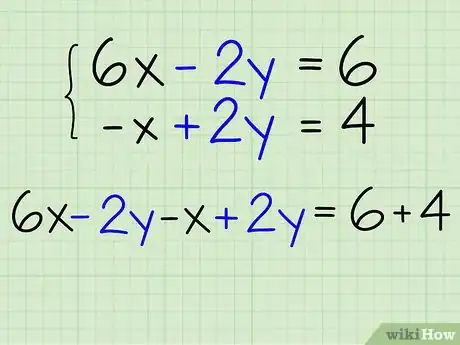

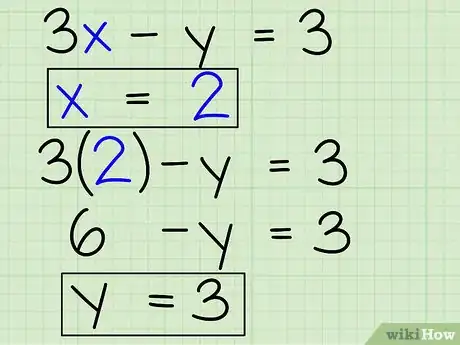
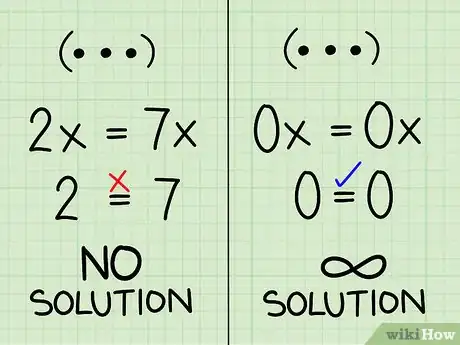
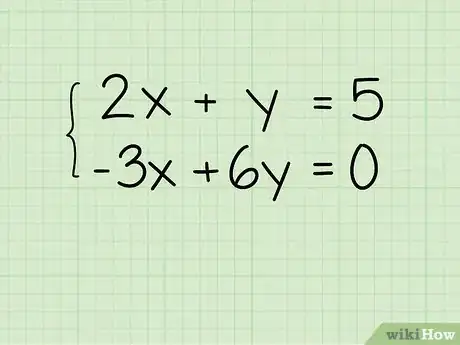
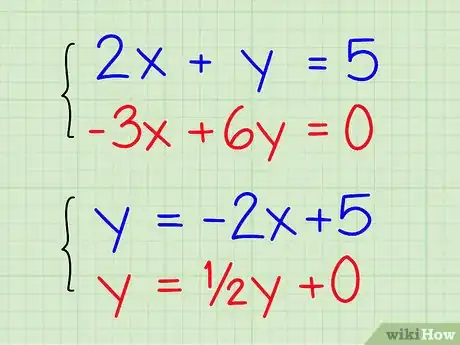
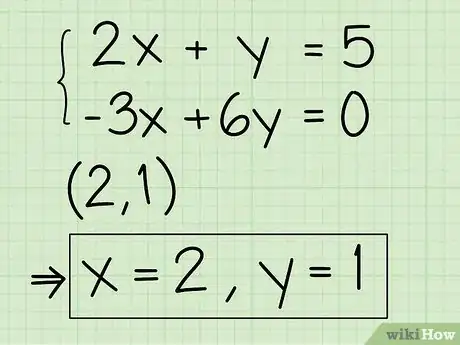



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
