wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 9 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 5 835 volte
La fattorizzazione in numeri primi permette di scomporre un numero nei suoi elementi di base. Se non ti piace lavorare con numeri grandi, come 5.733, puoi imparare a rappresentarli in maniera più semplice, ad esempio: 3 x 3 x 7 x 7 x 13. Questo tipo di processo è indispensabile nella crittografia o nelle tecniche che si utilizzano per garantire la sicurezza delle informazioni. Se non sei ancora pronto a sviluppare il tuo personale sistema di posta elettronica sicura, inizia a usare la scomposizione in fattori primi per semplificare le frazioni.
Passaggi
Scomporre in Fattori Primi
-
1Impara la fattorizzazione. È un processo di "scomposizione" di un numero in parti più piccole; queste parti (o fattori) generano il numero di partenza quando vengono moltiplicate tra loro.
- Per esempio, per scomporre il numero 18, puoi scrivere 1 x 18, 2 x 9 oppure 3 x 6.
-
2Ripassa i numeri primi. Un numero si dice primo quando è divisibile solamente per 1 e per se stesso; per esempio, il numero 5 è il prodotto di 5 e 1, non puoi scomporlo ulteriormente. Lo scopo della suddivisione in fattori primi è scomporre ogni valore finché non si ottiene una sequenza di numeri primi; tale processo si rivela molto utile quando si ha a che fare con le frazioni per semplificarne il confronto e l'utilizzo nelle equazioni.[1]
-
3Inizia con un numero. Scegline uno che non sia primo e maggiore di 3. Se usi un numero primo, non c'è alcun procedimento da svolgere, dato che non è scomponibile.
- Esempio: di seguito viene proposta la scomposizione in fattori primi di 24.
-
4Dividi il valore di partenza in due numeri. Trovane due che, moltiplicati tra loro, producono il numero di partenza. Puoi usare una coppia qualsiasi di valori, ma se uno dei due è un numero primo, puoi facilitare parecchio il procedimento. Una buona strategia è dividere il numero per 2, poi per 3, poi per 5 passando gradualmente ai numeri primi via via più grandi, finché non trovi un divisore perfetto.
- Esempio: se non conosci alcun fattore di 24, prova a dividerlo per un piccolo numero primo. Inizia con 2 e ottieni 24 = 2 x 12. Non hai ancora concluso il lavoro, ma è un buon punto di partenza.
- Dato che 2 è un numero primo, è un buon divisore con cui iniziare quando stai scomponendo un numero pari.
-
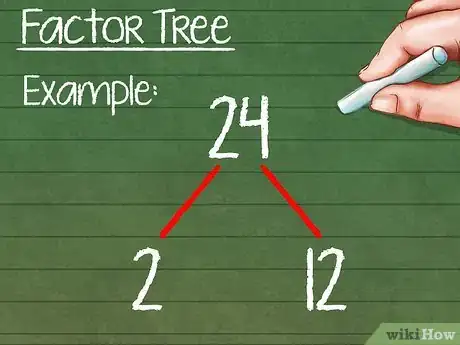
5Imposta uno schema di scomposizione. Si tratta di un metodo grafico che ti aiuta a organizzare il problema e a tenere traccia dei fattori.[2] Per cominciare, disegna due "rami" che si dividono dal numero originale, quindi annota i primi due fattori all'altra estremità di tali segmenti.
- Esempio:
- 24
- /\
- 2 12
-
6Procedi con l'ulteriore scomposizione dei numeri. Osserva la coppia di valori che hai trovato (la seconda riga dello schema) e chiediti se entrambi sono numeri primi. Se uno di essi non lo è, puoi dividerlo ulteriormente applicando sempre la medesima tecnica. Disegna altri due rami che partono dal numero e scrivi un'altra coppia di fattori nella terza riga.
- Esempio: 12 non è un numero primo, puoi quindi fattorizzarlo ulteriormente. Usa la coppia di valori 12 = 2 x 6 e aggiungila allo schema.
- 24
- /\
- 2 12
- /\
- 2 x 6
-
7Riporta il numero primo. Se uno dei due fattori della riga precedente è un numero primo, riscrivilo in quello sottostante usando un singolo "ramo". Non c'è modo di scomporlo ulteriormente, ti basta quindi tenerne semplicemente traccia.
- Esempio: 2 è un numero primo, riportalo dalla seconda alla terza riga.
- 24
- /\
- 2 12
- / /\
- 2 2 6
-
8Procedi in questo modo finché non ottieni solamente numeri primi. Controlla ogni riga non appena la scrivi; se contiene dei valori che possono essere divisi, procedi aggiungendo un altro livello. Hai terminato la scomposizione quanto ti ritrovi solamente con numeri primi.
- Esempio: 6 non è un numero primo e deve essere diviso nuovamente; 2 invece lo è, ti basta quindi riscriverlo nella riga successiva.
- 24
- /\
- 2 12
- / /\
- 2 2 6
- / / /\
- 2 2 2 3
-
9Scrivi la riga finale come sequenza di fattori primi. Alla fine, avrai numeri che possono essere divisi per 1 e per se stessi. Quando questo accade, il processo è concluso e la sequenza di valori primi che costituisce il numero iniziale deve essere riscritta sotto forma di moltiplicazione.
- Controlla il lavoro svolto moltiplicando tra loro i numeri che costituiscono l'ultima riga; il prodotto dovrebbe corrispondere al numero originale.
- Esempio: la riga finale dello schema di fattorizzazione contiene solo dei 2 e dei 3; entrambi sono numeri primi, hai quindi concluso la scomposizione. Puoi riscrivere il numero iniziale sotto forma di moltiplicazione di fattori: 24 = 2 x 2 x 2 x 3.
- L'ordine dei fattori non è importante, anche "2 x 3 x 2 x 2" è corretto.
-
10Semplifica la sequenza usando le potenze (facoltativo). Se sai utilizzare gli esponenti, puoi esprimere la scomposizione in fattori primi in maniera più semplice da leggere. Ricorda che una potenza è un numero con una base seguito da un esponente che indica il numero di volte in cui devi moltiplicare la base per se stessa.
- Esempio: nella sequenza 2 x 2 x 2 x 3, determina quante volte compare il numero 2. Dato che si ripete 3 volte, puoi riscrivere 2 x 2 x 2 come 23. L'espressione semplificata diventa: 23 x 3.
Pubblicità
Sfruttare la Scomposizione in Fattori Primi
-
1Trova il massimo comune divisore di due numeri. Questo valore (MCD) corrisponde al numero più grande che può dividere entrambi i numeri presi in considerazione. Di seguito, viene spiegato come trovare il MCD fra 30 e 36 sfruttando la scomposizione in fattori primi:
- Trova la fattorizzazione in numeri primi dei due numeri. La scomposizione di 30 è 2 x 3 x 5. Quella di 36 è 2 x 2 x 3 x 3.
- Trova il numero che compare in entrambe le sequenze. Cancellalo e riscrivi ciascuna moltiplicazione in un'unica riga. Per esempio, il numero 2 compare in entrambe le scomposizioni, puoi cancellarlo e riportare nella nuova riga un solo 2. In seguito restano 30 =
2x 3 x 5 e 36 =2x 2 x 3 x 3. - Ripeti il procedimento finché non ci sono più fattori comuni. Nelle sequenze c'è anche il numero 3, riscrivilo quindi sulla nuova riga per cancellare 2 e 3. Confronta 30 =
2 x 3x 5 e 36 =2x 2 x3x 3. Non ci sono altri fattori comuni. - Per trovare il MCD moltiplica tutti i fattori condivisi. In questo esempio c'è solo 2 e 3, quindi il massimo comune divisore è 2 x 3 = 6. Si tratta del numero maggiore che è fattore sia di 30 sia di 36.
-
2Semplifica le frazioni usando il MCD. Puoi sfruttarlo ogni volta che una frazione non è ridotta ai minimi termini. Trova il massimo comune divisore tra il numeratore e il denominatore come descritto in precedenza e in seguito dividi entrambe le parti della frazione per questo numero.[3] La soluzione è una frazione di pari valore, ma espressa nella forma semplificata.
- Per esempio, semplifica la frazione 30/36. Hai già trovato il MCD che è 6, procedi quindi con le divisioni:
- 30 ÷ 6 = 5
- 36 ÷ 6 = 6
- 30/36 = 5/6
-
3Trova il minimo comune multiplo fra due numeri. Si tratta del valore minimo (mcm) che annovera tra i suoi fattori entrambi i numeri in questione. Per esempio, il mcm di 2 e 3 è 6 perché quest'ultimo ha sia 2 sia 3 come fattori. Ecco come trovarlo con la fattorizzazione:
- Inizia a scomporre i due numeri in fattori primi. Per esempio, la sequenza di 126 è 2 x 3 x 3 x 7, mentre quella di 84 è 2 x 2 x 3 x 7.
- Verifica quante volte compare ciascun fattore; scegli la sequenza in cui è presente più volte e cerchialo. Ad esempio, il numero 2 compare una volta nella scomposizione di 126, ma due volte in quella di 84. Cerchia 2 x 2 nella seconda lista.
- Ripeti il processo per ogni singolo fattore. Per esempio, il numero 3 compare nella prima sequenza con maggiore frequenza, cerchia quindi 3 x 3. Il 7 è presente una volta sola in ogni elenco, devi quindi evidenziare un solo 7 (in questo caso non importa da quale sequenza lo scegli).
- Moltiplica tutti i numeri cerchiati tra loro e trova il minimo comune multiplo. Considerando l'esempio precedente, il mcm di 126 e 84 è 2 x 2 x 3 x 3 x 7 = 252. Questo è il numero più piccolo che ha come fattori sia 126 sia 84.
-
4Sfrutta il minimo comune multiplo per sommare le frazioni. Prima di procedere con questa operazione, devi manipolare le frazioni in modo che abbiano il medesimo denominatore. Trova il mcm fra i denominatori e moltiplica ogni frazione in modo che ciascuna abbia proprio il minimo comune moltiplicatore come denominatore; una volta espressi i numeri frazionali in questo modo, puoi sommarli.
- Per esempio, supponi di dover risolvere 1/6 + 4/21.
- Sfruttando il metodo descritto in precedenza, puoi trovare il mcm tra 6 e 21 che è 42.
- Trasforma 1/6 in una frazione con denominatore pari a 42. Per farlo, risolvi 42 ÷ 6 = 7. Moltiplica 1/6 x 7/7 = 7/42.
- Per trasformare 4/21 in una frazione con denominatore pari a 42, risolvi 42 ÷ 21 = 2. Moltiplica 4/21 x 2/2 = 8/42.
- Ora le frazioni hanno il medesimo denominatore e puoi sommarle facilmente: 7/42 + 8/42 = 15/42.
Pubblicità
Problemi Pratici
- Cerca di risolvere i problemi qui proposti da solo; quando credi di aver trovato il risultato corretto, evidenzia la soluzione per renderla visibile. Gli ultimi problemi sono più complessi.
- Scomponi 16 in fattori primi: 2 x 2 x 2 x 2
- Riscrivi la soluzione usando le potenze: 24
- Trova la fattorizzazione di 45: 3 x 3 x 5
- Riscrivi la soluzione sotto forma di potenze: 32 x 5
- Scomponi 34 in fattori primi: 2 x 17
- Trova la scomposizione di 154: 2 x 7 x 11
- Scomponi 8 e 40 in fattori primi e calcolane poi il massimo comune divisore: La scomposizione di 8 è 2 x 2 x 2 x 2; quella di 40 è 2 x 2 x 2 x 5; il MCD è 2 x 2 x 2 = 6.
- Trova la scomposizione in fattori primi di 18 e 52, calcolane in seguito il minimo comune multiplo: La scomposizione di 18 è 2 x 3 x 3; quella di 52 è 2 x 2 x 13; il mcm è 2 x 2 x 3 x 3 x 13 = 468.
Consigli
- Ogni numero può essere scomposto in un'unica sequenza di fattori primi. Non importa quali sono i fattori intermedi che utilizzi, alla fine otterrai tale rappresentazione specifica; questo concetto è chiamato teorema fondamentale dell'aritmetica.[4]
- Invece di riscrivere i numeri primi a ogni passaggio della scomposizione, puoi limitarti a cerchiarli. Al termine, tutti i numeri contrassegnati con un cerchio sono i fattori primi.
- Controlla sempre il lavoro svolto, potresti commettere degli errori banali e non accorgertene.
- Fai attenzione alle "domande trabocchetto"; se ti viene chiesto di scomporre un numero primo in fattori primi, non devi svolgere alcun calcolo.[5] I fattori primi di 17 sono semplicemente 1 e 17, non devi procedere ad alcuna suddivisione successiva.
- Puoi trovare il massimo comune divisore e il minimo comune multiplo di tre o più numeri.
Avvertenze
- Uno schema dei fattori non mostra tutti quelli possibili ma solo quelli primi.
Riferimenti
- ↑ http://www.eduplace.com/math/mw/background/6/03/te_6_03_fractions_ask.html
- ↑ http://study.com/academy/lesson/what-is-a-factor-tree-definition-example.html
- ↑ http://www.virtualnerd.com/tutorials/?id=Gr6_04_01_0014
- ↑ http://www.mathsisfun.com/numbers/fundamental-theorem-arithmetic.html
- ↑ http://www.mathsisfun.com/prime-factorization.html







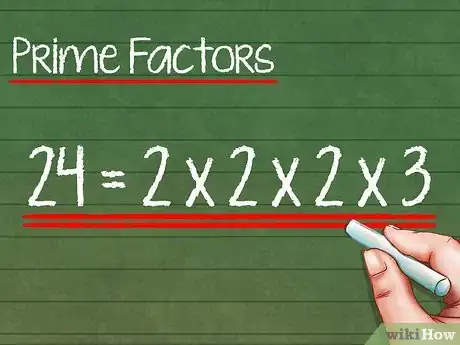








-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
