wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, autori volontari hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 9 700 volte
Le frazioni algebriche (o funzioni razionali) possono sembrare estremamente complesse a prima vista e assolutamente impossibili da risolvere agli occhi di uno studente che non le conosce. È difficile capire da dove iniziare osservando l'insieme di variabili, numeri ed esponenti; per fortuna, però, si applicano le medesime regole che si utilizzano per risolvere le normali frazioni, come 15/25.
Passaggi
Semplificare le Frazioni
-
1Impara la terminologia delle frazioni algebriche. Le parole descritte di seguito verranno usate in tutto il resto dell'articolo e sono molto comuni nei problemi che prevedono le funzioni razionali.
- Numeratore: la porzione superiore della frazione (ad esempio (x+5)/(2x+3)).
- Denominatore: la porzione inferiore della frazione (ad esempio (x+5)/(2x+3)).
- Denominatore comune: è il numero che divide in maniera perfetta sia il numeratore sia il denominatore; per esempio, considerando la frazione 3/9, il denominatore comune è 3, dato che divide entrambi i numeri in maniera perfetta.
- Fattore: un numero che, moltiplicato per un altro, permette di ottenerne un terzo; per esempio, i fattori di 15 sono 1, 3, 5 e 15; i fattori di 4 sono 1, 2 e 4.
- Equazione semplificata: la forma più semplice di una frazione, di una equazione o di un problema che si ottiene elidendo tutti i fattori comuni e raggruppando le variabili simili tra loro (5x + x = 6x). Se non puoi procedere con ulteriori operazioni matematiche, significa che la frazione è semplificata.
-
2Ripassa il metodo per risolvere le frazioni semplici.[1] Questi sono i passaggi esatti che devi utilizzare per semplificare anche quelle algebriche. Considera l'esempio di 15/35; per semplificare questa frazione, devi trovare il denominatore comune che, in questo caso, è 5. Così facendo, puoi elidere tale fattore:
15 → 5 * 3
35 → 5 * 7
Ora puoi cancellare i termini simili; nel caso specifico di questa frazione, puoi elidere i due "5" e lasciare la frazione semplificata 3/7. -
3Togli i fattori dalla funzione razionale come se fossero dei normali numeri.[2] Nell'esempio precedente, hai potuto elidere facilmente il numero 5 e puoi applicare il medesimo principio nelle espressioni più complesse, come 15x – 5. Trova un fattore che i due numeri hanno in comune; in tal caso è 5, dato che puoi dividere sia 15x sia -5 proprio per questa cifra. Come nell'esempio precedente, rimuovi il fattore comune e moltiplicalo per i termini "rimasti":
15x – 5 = 5 * (3x – 1) Per verificare le operazioni, moltiplica nuovamente 5 per il resto dell'espressione; otterrai i numeri da cui sei partito. -
4Sappi che puoi eliminare i termini complessi proprio come quelli semplici. In questo genere di problema vale il medesimo principio utilizzato per le frazioni comuni. Questo è il metodo più elementare per semplificare le frazioni durante i calcoli.[3] Considera l'esempio:
(x+2)(x-3)(x+2)(x+10) Osserva che il termine (x+2) è presente sia al numeratore sia al denominatore; di conseguenza, puoi eliderlo proprio come hai cancellato il 5 da 15/35:(x+2)(x-3) → (x-3)(x+2)(x+10) → (x+10)Pubblicità
Semplificare le Frazioni Algebriche
-
1Trova il fattore comune al numeratore, la parte superiore della frazione. La prima cosa da fare quando si "manipola" una funzione razionale è semplificare ogni parte che la compone; inizia dal numeratore, suddividendolo nel maggior numero possibile di fattori.[4] Considera questo esempio:
9x-315x+6 Inizia dal numeratore: 9x – 3; puoi notare che esiste un fattore comune per entrambi i numeri ed è 3. Procedi come faresti con qualsiasi altro numero, "portando fuori" il 3 dalle parentesi e scrivendo 3 * (3x-1); così facendo, ottieni il nuovo numeratore:3(3x-1)15x+6 -
2Trova il fattore comune al denominatore.[5] Continuando con l'esempio precedente, isola il denominatore, 15x+6 e cerca un numero che può dividere entrambi i valori in maniera perfetta; in tal caso, si tratta del numero 3, che ti permette di riformulare il termine come 3 * (5x +2). Scrivi il nuovo numeratore:
3(3x-1)3(5x+2) -
3Elidi i termini simili. Questa è la fase in cui procedi alla vera semplificazione della frazione. Cancella ogni numero che compare sia al denominatore sia al numeratore; nel caso dell'esempio, elidi il numero 3:
3(3x-1) → (3x-1)3(5x+2) → (5x+2) -
4Devi capire quando la frazione è ridotta ai minimi termini. Puoi affermarlo quando non ci sono altri fattori comuni da elidere. Ricorda che non puoi eliminare quelli che si trovano nelle parentesi; nel problema precedente, non puoi cancellare la variabile "x" di 3x e 5x, dato che i termini sono in realtà (3x -1) e (5x + 2). Di conseguenza, la frazione è completamente semplificata e puoi annotare il risultato:
3(3x-1)
3(5x+2) -
5Risolvi un problema. Il modo migliore per imparare a semplificare le frazioni algebriche è continuare a esercitarsi. Puoi trovare le soluzioni subito dopo i problemi:
4(x+2)(x-13) Soluzione: (x=13)
(4x+8)2x2-x Soluzione:(2x-1)/5
5xPubblicità
Trucchi per i Problemi Complessi
-
1Trova l'opposto della frazione raccogliendo i fattori negativi. Supponi di avere l'equazione:
3(x-4)5(4-x) Osserva che (x-4) e (4-x) sono "quasi" identici, ma non puoi eliderli perché sono l'uno l'opposto dell'altro; tuttavia, puoi riscrivere (x - 4) come -1 * (4 - x), proprio come puoi riformulare (4 + 2x) in 2 * (2 + x). Questa procedura si chiama "raccogliere il fattore negativo".-1 * 3(4-x)5(4-x) Ora puoi eliminare facilmente i due termini identici (4-x)-1 * 3 lasciando il risultato -3/5.(4-x)5(4-x) -
2Riconosci le differenze fra quadrati quando lavori con queste frazioni. Si tratta in pratica di un numero elevato al quadrato a cui viene sottratto un altro numero alla potenza di 2, proprio come l'espressione (a2 - b2). La differenza fra due quadrati perfetti si semplifica sempre riscrivendola come moltiplicazione fra la somma e la differenza delle radici; in ogni caso, puoi semplificare la differenza di quadrati perfetti in questo modo:
a2 - b2 = (a+b)(a-b) Si tratta di un "trucco" estremamente utile quando cerchi termini simili in una frazione algebrica.- Esempio: x2 - 25 = (x+5)(x-5).
-
3Semplifica le espressioni polinomiali. Si tratta di espressioni algebriche complesse, che contengono più di due termini, ad esempio x2 + 4x + 3; per fortuna, molte di queste possono essere semplificate usando la scomposizione in fattori. L'espressione descritta in precedenza può essere formulata come (x+3)(x+1).
-
4Ricorda che puoi scomporre in fattori anche le variabili. Questo metodo è molto utile soprattutto con le espressioni esponenziali, ad esempio x4 + x2. Puoi eliminare l'esponente maggiore come un fattore; in tal caso: x4 + x2 = x2(x2 + 1).Pubblicità
Consigli
- Quando raccogli i fattori controlla il lavoro svolto eseguendo la moltiplicazione, per assicurarti di ritrovare il termine di partenza.
- Cerca di raccogliere il maggior fattore comune per semplificare completamente l'equazione.
Avvertenze
- Se dimentichi le proprietà delle potenze, non sarai in grado di risolvere questi problemi; per tale motivo, devi memorizzarle a ogni costo.

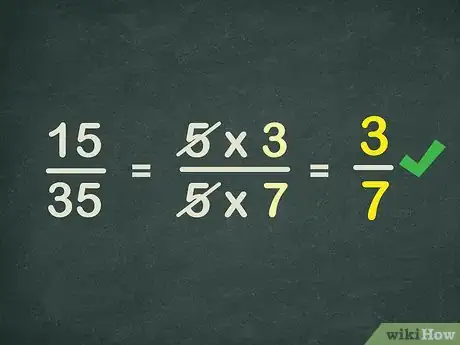

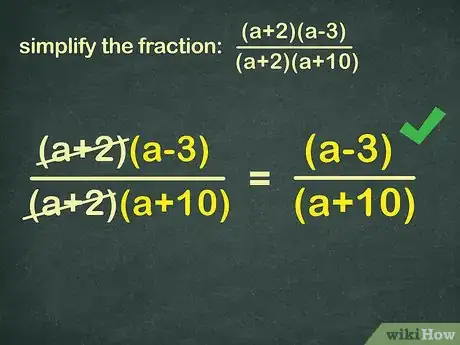
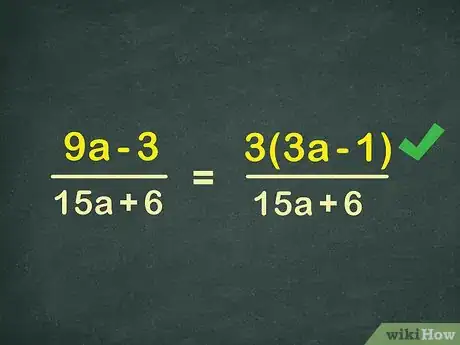
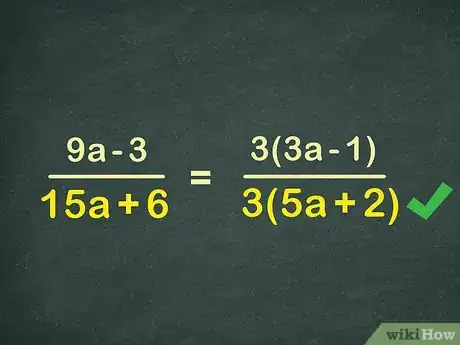
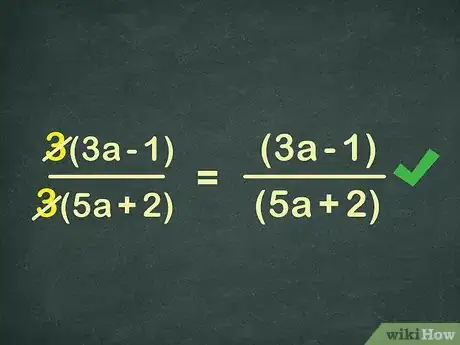
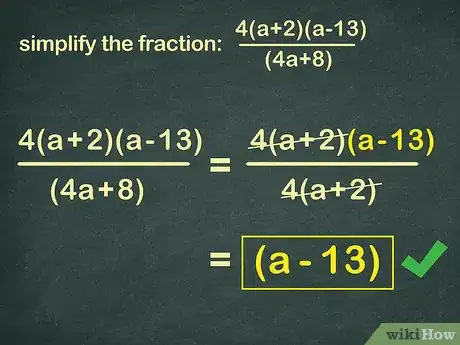
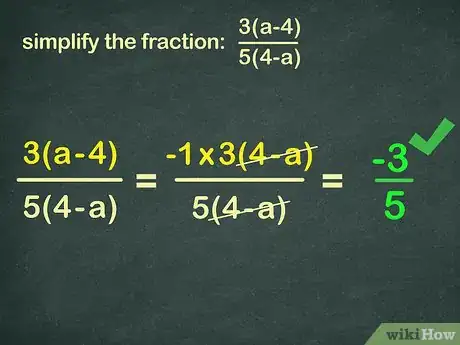
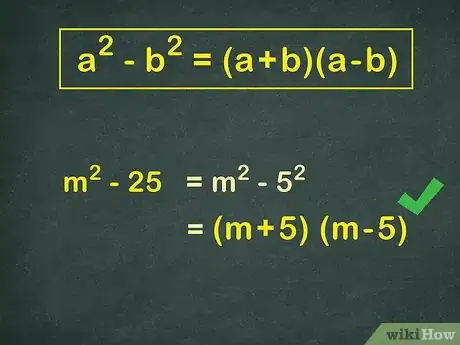

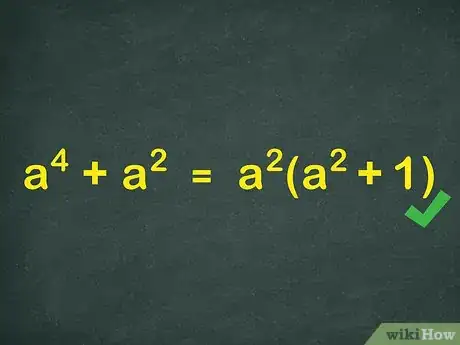



-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
