Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 9 578 volte
La moltiplicazione del contadino russo è una tecnica interessante che permette di svolgere i calcoli raddoppiando e dimezzando i numeri.[1] Proprio come la normale divisione e moltiplicazione, si tratta di un algoritmo che consente di trovare il prodotto di qualsiasi coppia di numeri interi utilizzando solamente delle divisioni e moltiplicazioni per 2.[2] Sebbene non sia un metodo rapido quanto quello standard, è però divertente da provare.
Passaggi
Primo Esempio
-
1Pensa a due numeri che vuoi moltiplicare. Scegli una coppia di valori che ti permetta di risolvere un determinato problema o solo per fare un tentativo con il metodo del contadino russo.
- Ad esempio, cerca di moltiplicare 146 x 37.
-
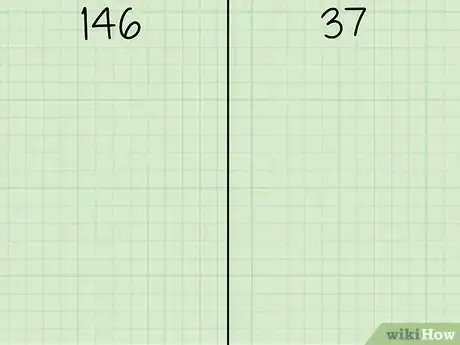
2Realizza due colonne. Prendi carta e penna e dividi il foglio in due parti, tracciando una riga verticale nel mezzo; scrivi ciascun numero che vuoi moltiplicare all'inizio di ogni colonna.[3]
- Per l'esempio considerato, scrivi "146" alla sommità della prima metà e "37" nella seconda.
-
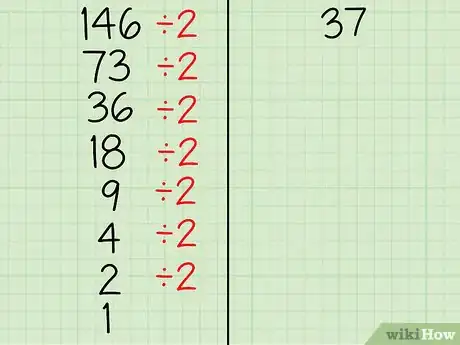
3Dimezza più volte il numero della colonna di sinistra.[4] Dividi ripetutamente il valore che hai scritto all'inizio della colonna di sinistra per 2 finché non ottieni 1. Ignora eventuali resti quando incontri un valore dispari e scrivi i numeri dimezzati, in maniera ordinata, lungo la colonna. Per esempio:
- Inizia dimezzando 146 (146 ÷ 2 = 73). Scrivi "73" sotto "146" nella prima colonna;
- Prosegui dividendo 73 ÷ 2 = 36 con il resto di 1. Annota solamente "36" sotto "73" ignorando il resto;
- Successivamente dimezza 36 (36 ÷ 2 = 18). Riporta "18" sotto "36";
- Continua dividendo 18 ÷ 2 = 9 e scrivendo "9" sotto "18";
- Dimezza 9 (9 ÷ 2 = 4 con il resto di 1). Scrivi "4" nella colonna sinistra sotto il "9" omettendo il resto;
- In seguito dimezza 4 e ottieni 2. Scrivi il numero sotto "4";
- Infine, procedi con 2 (2÷ 2 = 1). Scrivi "1" sotto il "2".
-
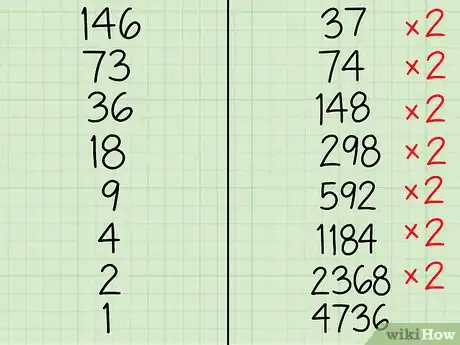
4Raddoppia il valore di destra finché le due colonne non hanno la medesima lunghezza.[5] Moltiplica il secondo fattore per 2 tante volte quante hai diviso il primo fattore. Per esempio:
- Ciascuna colonna dovrebbe contenere 8 numeri, dato che hai dovuto eseguire sette divisioni per ridurre il primo fattore a "1".
- Inizia a raddoppiare il numero della seconda colonna: 37 x 2 = 74. Riporta "74" sotto "37";
- Esegui poi l'operazione 74 x 2 = 148 annotando "148" nella colonna di destra sotto "74";
- Raddoppia 148 ottenendo 296. Scrivi il risultato sotto "148";
- Continua con lo stesso criterio e ottieni 296 x 2 = 592; riporta "592" sotto "296";
- Raddoppia 592 per ottenere 1184 e scrivi il risultato sotto "592";
- Esegui un'altra moltiplicazione: 1184 x 2 = 2368. Scrivi "2368" nella colonna di destra sotto "1184";
- Infine raddoppia per l'ultima volta: 2368 x 2 = 4736. Scrivi "4736" sul fondo della colonna di destra.
-
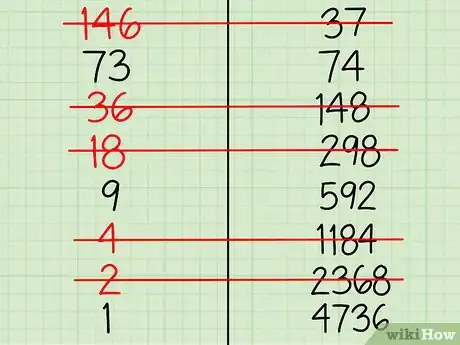
5Depenna tutte le righe che hanno un numero pari nella colonna di sinistra.[6] Usa la biro e traccia una linea orizzontale sulle coppie composte da un numero pari nella colonna di sinistra:
- Ci sono 8 righe e devi eliminarne 5;
- Depenna quelle che contengono 146, 36, 18, 4 e 2 nella colonna a sinistra, in quanto sono tutti valori pari. Questo significa cancellare la prima riga (146;37), la terza (36;148), la quarta (18;296), la sesta (4;1184) e la settima (2;2368).
- Ricorda che devi cancellare le righe che contengono un numero pari, anche se questo inizia con una cifra dispari. Per esempio, dovresti depennare la prima riga che riporta 146, dato che è un valore pari (fa fede l'ultima cifra) anche se inizia con "1" (dispari); per la stessa ragione, devi eliminare la coppia con "36", perché è un numero divisibile per due nonostante inizi per "3".
- Se preferisci, puoi semplicemente depennare i numeri del lato destro accoppiati a un valore pari sul lato sinistro; in tal caso, devi cancellare quelli che ricadono nella prima, terza, quarta, sesta e settima riga: 37, 148, 296, 1184 e 2368.
-
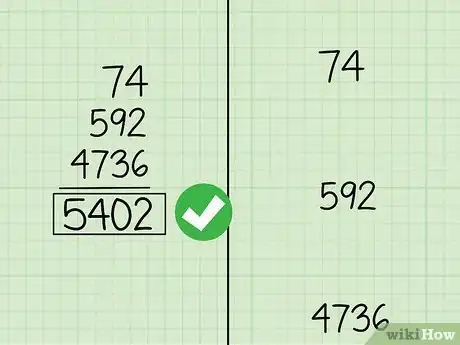
6Calcola la somma dei numeri rimanenti nella colonna a destra.[7] Somma i valori che non hai depennato. Il totale è pari al prodotto che avresti trovato moltiplicando i due fattori originali con il metodo standard. Nell'esempio considerato:
- I numeri rimasti nella colonna di destra sono: 74, 592, 4736;
- Sommandoli ottieni: 74 + 592 + 4736 = 5402;
- Il valore corrisponde al prodotto dei primi due fattori originali 146 e 37: 146 x 37 = 5402.
Pubblicità
Risoluzione dei Problemi
-
1Svolgi la moltiplicazione con carta e penna per verificare il risultato. Puoi usare il metodo standard per la moltiplicazione in colonna per accertarti che il prodotto ottenuto con quello del contadino russo sia corretto. Considerando l'esempio precedente 146 x 37:
- Scrivi prima "146" e poi "37" sotto di esso, allineando le unità, le decine e via dicendo;
- Traccia una linea orizzontale sotto il secondo numero per organizzare lo spazio di lavoro. Devi svolgere i calcoli sotto tale linea;
- Moltiplica 7 x 6 = 42. Scrivi "2" nello spazio di lavoro e riporta "4";
- Calcola 7 x 4 = 28. Aggiungi il riporto "4" e ottieni 4 + 28 = 32. Annota "2" nello spazio di lavoro a sinistra del primo "2" e riporta "3";
- Moltiplica 7 x 1 = 7. Somma il riporto "3" e ottieni "10". Scrivilo nello spazio di lavoro a sinistra del "22" già annotato;
- Dovresti avere il valore "1022" nello spazio di lavoro;
- Continua il calcolo nella riga sottostante, direttamente sotto "1022";
- Scrivi "0" alla destra di questa nuova riga proprio sotto il "2" delle unità di "1022";
- Moltiplica 3 x 6 = 18. Annota "8" a sinistra dello "0" e riporta "1";
- Svolgi il calcolo 3 x 4 = 12; somma il riporto "1" e ottieni "13". Annota "3" alla sinistra di "8" e riporta "1";
- Svolgi l'ultima moltiplicazione 3 x 1 = 3. Aggiungi il riporto di "1": 3 + 1 = 4;
- A questo punto, nella seconda riga dello spazio di lavoro dovresti avere il valore "4380";
- Somma i numeri delle due righe dello spazio di lavoro: 1022 + 4380. Dovresti ottenere "5402".
- Questa somma, che corrisponde al prodotto ottenuto con il metodo del contadino russo, dimostra che la tecnica precedente ha portato al risultato corretto.
-
2Verifica il risultato con la calcolatrice. Puoi anche usare un dispositivo elettronico per assicurarti che il prodotto risultante dal metodo russo sia giusto. Considera sempre l'esempio precedente (146 x 37):
- Digita "146" sulla calcolatrice premendo i tasti delle cifre corrispondenti: 1, 4, 6;
- Premi il tasto di moltiplicazione ("x");
- Inserisci "37" premendo gli opportuni tasti: 3, 7;
- Premi il tasto di uguaglianza ("=").
- Sullo schermo dovrebbe comparire il risultato "5402" che corrisponde al valore che hai calcolato in precedenza e che ti conferma la correttezza dei calcoli.
-
3Ricomincia da capo se commetti un errore. Se controllando il risultato ti rendi conto che non è corretto, cerca di trovare il passaggio in cui hai sbagliato e prova a eseguire nuovamente il processo con il metodo russo.
- Per prima cosa, cerca di controllare nuovamente il tuo lavoro con la calcolatrice o la tecnica standard per essere certo dei valori che hai ottenuto.
- In seguito, ripercorri i passaggi che hai svolto con il metodo del contadino russo.
- In questa fase, controlla due volte i calcoli per accertarti di non avere dimezzato o raddoppiato i numeri in maniera sbagliata.
- Inoltre, verifica la somma fra i valori rimasti nella colonna di destra dopo aver depennato tutti gli altri.
- Controlla scrupolosamente ogni passaggio per assicurarti che le soluzioni siano giuste.
-
4Se incontri delle difficoltà, chiedi aiuto a qualcun altro. Se non riesci a trovare la soluzione giusta o non sai come controllare il lavoro, chiedi aiuto a un amico, un fratello, un genitore o all'insegnante; questi può provare a svolgere i calcoli e confrontare poi i vari passaggi con quelli che hai fatto tu. Potrebbe anche spiegarti come utilizzare il metodo russo.
-
5Comprendi come funziona la tecnica.[8] In pratica, il sistema converte il problema in una moltiplicazione binaria (in base 2) invece che in base 10 (come avviene con il metodo tradizionale). Questo si ottiene dimezzando e moltiplicando i valori, dato che tali processi convertono qualsiasi numero in multipli di 2 o fattori.
-
6Sappi quando il metodo del contadino russo è utile. Devi utilizzarlo a volte durante un compito scolastico, se l'enunciato del problema richiede espressamente la sua applicazione oppure puoi decidere di farlo solo per divertimento; tuttavia, tale tecnica ha dei vantaggi che potrebbero rivelarsi utili in alcune applicazioni pratiche.
- Non c'è bisogno di conoscere o imparare a memoria le tabelline per riuscire a sfruttare tale metodo (come invece accade quando svolgi una moltiplicazione in colonna). Fintanto che sei capace di moltiplicare e dividere per 2, puoi trovare il prodotto di due fattori.
- Sono necessari pochi materiali per svolgere i calcoli con il metodo russo, che si rivela utile quando non hai a disposizione una calcolatrice o carta e penna. Ad esempio, potresti eseguire la moltiplicazione descritta nella sezione precedente (146 x 37) usando dei fagioli o altri oggetti analoghi. Ogni volta che devi dimezzare o raddoppiare un numero, ti basta aggiungere o togliere il corrispondente numero di fagioli.
- Tale tecnica richiede però più tempo rispetto al metodo standard.
- Inoltre, si rivela parecchio "scomoda" quando devi moltiplicare fattori grandi, in quanto prevedono parecchi multipli di 2 o contengono diversi fattori divisibili per 2.
Pubblicità
Riferimenti
- ↑ http://scimath.unl.edu/MIM/files/MATExamFiles/WestLynn_Final_070411_LA.pdf
- ↑ Gimmestad, Beverly J.. “The Russian Peasant Multiplication Algorithm: A Generalization”. The Mathematical Gazette 75.472 (1991): 169–171.
- ↑ http://scimath.unl.edu/MIM/files/MATExamFiles/WestLynn_Final_070411_LA.pdf
- ↑ http://scimath.unl.edu/MIM/files/MATExamFiles/WestLynn_Final_070411_LA.pdf
- ↑ http://scimath.unl.edu/MIM/files/MATExamFiles/WestLynn_Final_070411_LA.pdf
- ↑ http://scimath.unl.edu/MIM/files/MATExamFiles/WestLynn_Final_070411_LA.pdf
- ↑ http://scimath.unl.edu/MIM/files/MATExamFiles/WestLynn_Final_070411_LA.pdf
- ↑ http://www.wolframalpha.com/input/?i=russian+multiplication





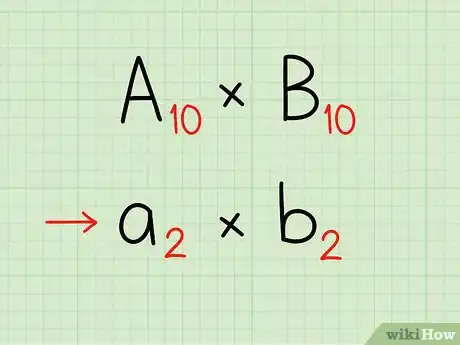




-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 9 578 volte