Questo articolo è stato scritto in collaborazione con il nostro team di editor e ricercatori esperti che ne hanno approvato accuratezza ed esaustività.
Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità.
Questo articolo è stato visualizzato 3 763 volte
Il sistema di assi cartesiani è piuttosto familiare e semplice da imparare, ma non si rivela sempre comodo in tutte le occasioni. Come ti comporteresti se volessi tracciare il grafico dei raggi di una ruota o il movimento dell'acqua in uno scarico? In questo caso, un sistema circolare si presta meglio alla situazione; infatti, utilizzi già un concetto elementare di coordinate polari nella tua vita quotidiana.[1] Per esempio, se vuoi trovare l'origine del suono di una sirena, hai bisogno di due informazioni: la sua distanza e la direzione da cui proviene. Un sistema di coordinate polari mappa i punti nello stesso modo descrivendo la distanza da un punto fisso e l'angolo da un raggio definito.
Passaggi
Tracciare le Coordinate Polari
-
1Prepara un piano polare. Probabilmente, hai già individuato dei punti con coordinate cartesiane usando la notazione per definirli all'interno di uno schema a griglia. Le coordinate polari utilizzano un grafico diverso basato sulle circonferenze:[2]
- Il centro del grafico (chiamato "origine" in un sistema cartesiano) è il polo e puoi identificarlo con la lettera O.
- Partendo dal polo, disegna una linea retta orizzontale verso destra. Questa è l'asse polare e puoi suddividerla in unità, proprio come faresti con l'asse delle x di un normale grafico cartesiano.
- Se hai un foglio di carta specifico per riportare le coordinate polari, potrebbero essere già presenti diverse circonferenze di varie dimensioni, tutte centrate nel polo; se utilizzi invece un normale foglio di carta bianca, non devi tracciarle.
-
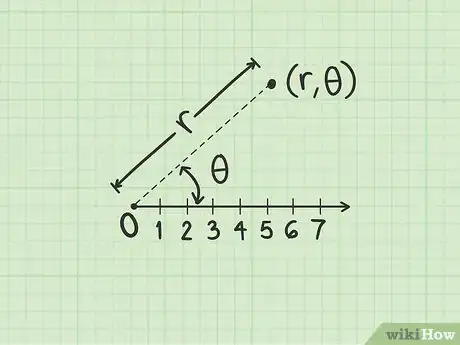
2Comprendi il concetto di coordinate polari. Su un sistema di riferimento polare ogni punto viene definito da una coppia di coordinate espresse nella forma :
- La prima variabile, , indica il raggio, o coordinata radiale; significa che il punto definito si trova sulla circonferenza di raggio centrata sul polo (origine).
- La seconda variabile, , rappresenta l'angolo, o coordinata angolare; significa che il punto si trova sulla linea che attraversa il polo e forma un angolo pari a con l'asse polare.
-
3Ripassa la circonferenza unitaria. Quando si considerano le coordinate polari, l'angolo è in genere espresso in radianti al posto dei gradi. In questo sistema, una rotazione completa (360° o angolo giro) corrisponde a un'ampiezza di 2 radianti. Questo valore è stato scelto perché la circonferenza di un cerchio con raggio pari a 1 unità misura 2 unità; prendendo dimestichezza con tali concetti puoi lavorare più facilmente con le coordinate polari.
- Se il libro di testo esprime gli angoli in gradi, non preoccuparti per il momento; è possibile riportare le coordinate polari utilizzando anche dei valori in gradi per .
Pubblicità
Disegnare un Punto
-
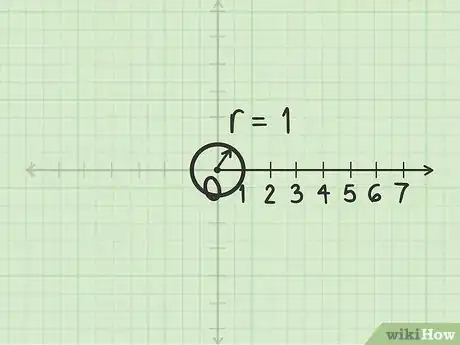
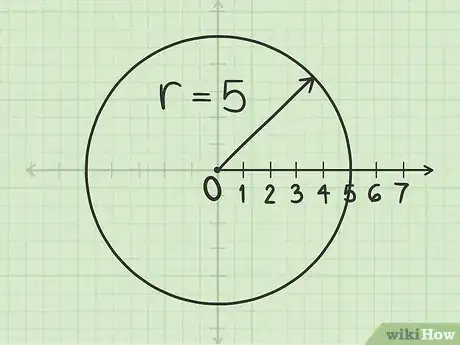
1Disegna una circonferenza con raggio pari a . Ogni punto che appartiene alla circonferenza possiede delle coordinate polari espresse nella forma . Inizia quindi a tracciare il cerchio di raggio e centrato sul polo.
- Il polo è il punto centrale del grafico, il medesimo in cui metteresti l'origine di un piano cartesiano.
- Per esempio, per disegnare il punto , punta il compasso nel polo, divarica l'asta con la mina di cinque unità lungo l'asse polare e fai ruotare lo strumento per tracciare il cerchio.
-
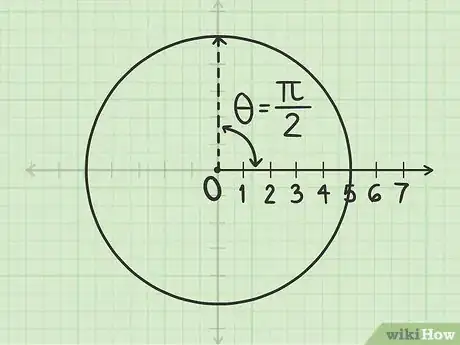
2Misura l'angolo dall'asse polare. Appoggia il goniometro facendo coincidere il suo centro con il polo; misura quindi l'ampiezza dell'angolo partendo dall'asse. Se l'angolo è espresso in radianti e lo strumento è tarato solamente in gradi, puoi convertire le unità di misura o far riferimento alla circonferenza unitaria per un aiuto.
- Per quanto riguarda il punto , grazie alla circonferenza unitaria puoi capire che corrisponde a 1/4 di giro, cioè a un angolo di 90° dall'asse polare.
- Misura sempre gli angoli positivi muovendoti in senso antiorario rispetto all'asse polare; gli angoli negativi si misurano in senso orario.
-
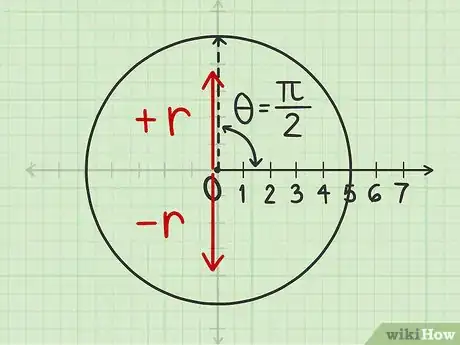
3Disegna una linea in base al segno di . La fase successiva consiste nel disegnare una linea che delimita l'angolo misurato; prima di procedere, però, devi sapere in quale direzione tracciarla. Osserva le coordinate polari per capire:
- Se è positivo, disegna una linea "in avanti" dal polo fino al segno dell'angolo che hai appena delineato.
- Se è negativo, traccia una linea "all'indietro" partendo dal segno dell'angolo sulla circonferenza fino al polo e proseguendo verso il lato opposto.
- Non farti confondere dalle coordinate cartesiane, il concetto di raggio positivo o negativo non corrisponde agli assi "x" e "y" negativi o positivi.
-
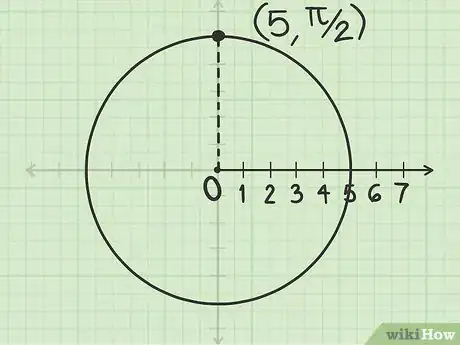
4Individua il punto in cui la linea retta e la circonferenza si intersecano. Questo è il punto con coordinate polari .
- Il punto si trova su una circonferenza di raggio 5 centrata nel polo a 1/4 di giro in senso antiorario partendo dell'asse polare; le coordinate cartesiane equivalenti sono (0;5).
Pubblicità
Esempi
Primo Esempio
Disegna il punto P corrispondente alle coordinate su un piano polare.
-
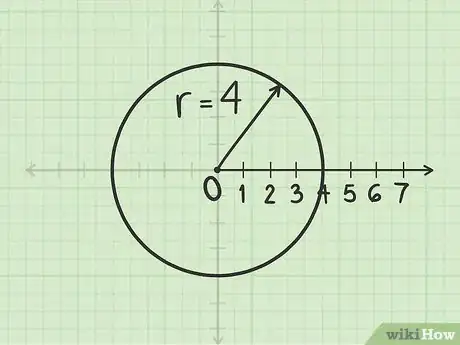
1Traccia una circonferenza di raggio . Stabilisci che il polo sia il suo centro.
-
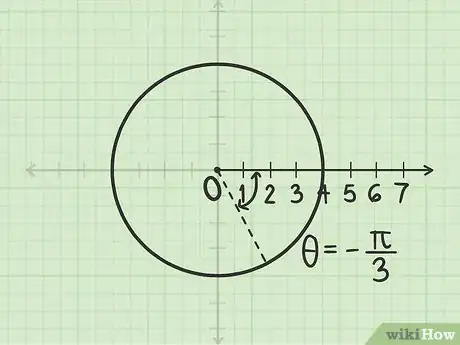
2Misura un angolo pari a radianti. Inizia la misurazione dall'asse polare (equivalente a quello delle ascisse); dato che l'angolo è negativo, devi seguire il senso orario.
-
3Disegna una linea che delimita tale angolo insieme all'asse polare. Inizia a tracciarla dal polo; dato che il raggio è positivo, il punto di intersezione fra la linea e la circonferenza è .Pubblicità
Secondo Esempio
Traccia il punto Q corrispondente a su un piano polare.
-
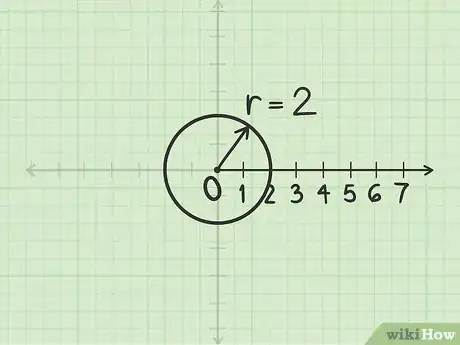
1Costruisci la circonferenza di raggio . Usa il polo come centro della stessa; sebbene il raggio sia un numero negativo, in questa fase il segno non ha importanza.
-
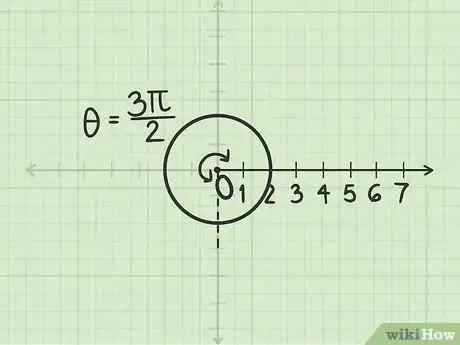
2Misura l'angolo di radianti. Dato che si tratta di un valore positivo, devi seguire il senso antiorario partendo dall'asse polare.
-
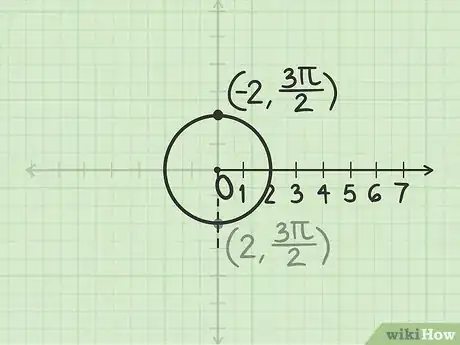
3Disegna la linea opposta all'angolo. Il raggio è un numero negativo, , devi quindi tracciare la linea partendo dal polo, ma in direzione diametralmente opposta rispetto all'angolo che hai appena misurato. Il punto di intersezione fra la circonferenza e la linea corrisponde alle coordinate polari .Pubblicità
Convertire le Coordinate Cartesiane in Polari
-
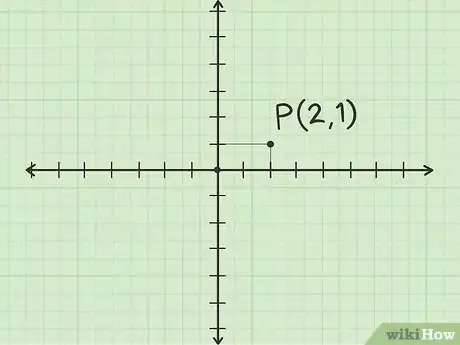
1Considera il punto su un piano cartesiano. Traccia un segmento pari a 2 unità lungo l'asse delle ascisse (x) partendo dall'origine. Da questo riferimento disegna un secondo segmento pari a 1 unità e parallelo alla direzione positiva dell'asse delle ordinate (y); hai quindi localizzato il punto (2, 1) e puoi etichettarlo con la lettera P.
-
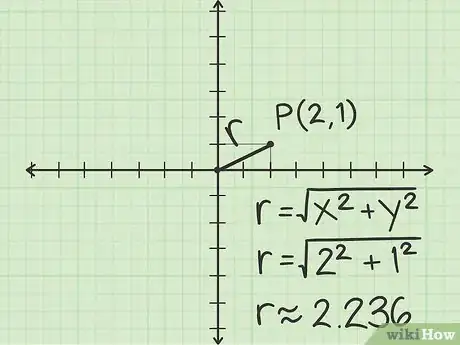
2Trova la distanza fra l'origine e . Disegna un segmento che unisce i due punti e che corrisponde al raggio delle coordinate polari. Questo segmento è anche l'ipotenusa di un triangolo rettangolo, di conseguenza puoi calcolarne la lunghezza sfruttando i teoremi di geometria. Ad esempio:
- I cateti del triangolo hanno lunghezze pari a 2 e 1 unità.
- Puoi trovare l'ipotenusa usando il teorema di Pitagora: .
- La formula generale per trovare dalle coordinate cartesiane è: , dove è la coordinata delle ascisse e quella delle ordinate.
-
3Trova l'angolo compreso tra e il segmento positivo dell'asse delle x. Sfrutta la trigonometria per trovare questo valore:
-
- La formula generale per trovare è , dove è la coordinata cartesiana delle ordinate e è quella delle ascisse.
-
-
4Scrivi le coordinate polari. A questo punto, hai trovato i valori di e . Le coordinate cartesiane (2, 1) corrispondono approssimativamente a quelle polari (2,24; 26,6º) o a quelle precise .Pubblicità
Consigli
- Memorizzare la circonferenza unitaria, saper convertire i radianti in gradi e viceversa sono abilità molto utili quando si deve tracciare un grafico con coordinate polari.
- Diversamente da quanto accade in un sistema di riferimento cartesiano, un punto ha infinite coordinate polari. Per esempio, il punto definito con (1, 2π) coincide con quello che ha coordinate (-1, π); inoltre, è il medesimo punto di (1, 4π), (1, 6π), (1, 8π) e così via. Ciascuna coppia di coordinate definisce quante volte devi completare un angolo giro, ma alla fine ti ritrovi sempre nella medesima posizione.[3]
Cose che ti Serviranno
- Foglio di carta
- Matita
- Compasso
- Goniometro












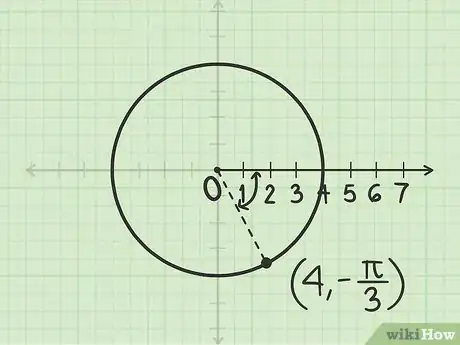










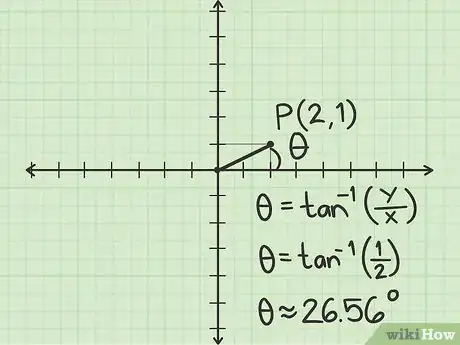




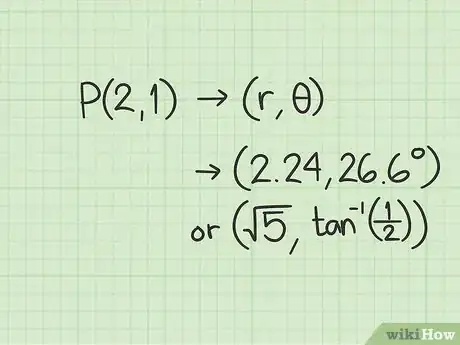




-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)

Il Content Management Team di wikiHow controlla con cura il lavoro dello staff di redattori per assicurarsi che ogni articolo incontri i nostri standard di qualità. Questo articolo è stato visualizzato 3 763 volte