Questo articolo è stato co-redatto da Jake Adams. Jake Adams è un tutor accademico e titolare di PCH Tutors, un'attività con sede a Malibù, in California, che offre tutoraggio e risorse di apprendimento per aree disciplinari che vanno dalla scuola materna all'università, preparazione SAT e ACT (test per l'ammissione ai college statunitensi) e consulenze in materia di ammissione ai college. Con oltre 11 anni di esperienza nel settore, Jake è anche il CEO di Simplifi EDU, un servizio di tutoraggio online il cui scopo è quello di fornire ai clienti accesso a una rete di eccellenti tutor californiani. Jake ha conseguito una laurea in Business Internazionale e Marketing presso la Pepperdine University.
Questo articolo è stato visualizzato 31 468 volte
Diversamente da una linea retta, l'inclinazione di una curva cambia costantemente spostandosi lungo il grafico. Il calcolo infinitesimale introduce gli studenti all'idea che ciascun punto del grafico possa essere descritto con una pendenza, o un "tasso di variazione istantaneo". La tangente è una retta con la stessa inclinazione, che passa precisamente per quel punto del grafico. Per trovare la sua equazione, devi sapere come trovare la derivata della funzione originale.
Passaggi
Trovare l'Equazione della Retta Tangente
-
1Disegna la funzione e la retta tangente (consigliato). Con un grafico, sarà più facile seguire il problema e verificare se la tua risposta ha senso. Disegna la funzione su carta quadrettata, usando una calcolatrice grafica come riferimento se necessario. Traccia anche la tangente che attraversa il punto di interesse, ricordando che si tratta della retta che attraversa quel punto, con la stessa inclinazione della funzione.
-
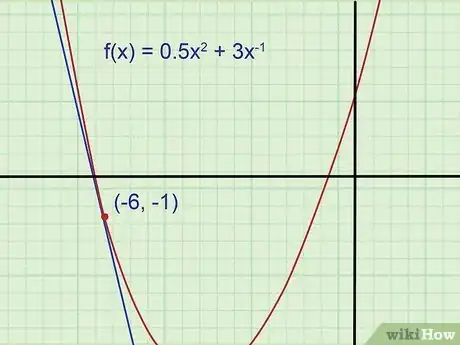
Esempio 1. Disegna il grafico della parabola . Disegna la tangente che attraversa il punto (-6, -1).
Non conosci ancora l'equazione di questa retta, ma puoi già capire che la pendenza è negativa e che l'intercetta verticale è negativa (ben al di sotto del vertice della parabola che ha valore y pari a -5,5). Se la tua risposta finale non rispetta queste condizioni, saprai di aver commesso un errore.
-
Esempio 1. Disegna il grafico della parabola . Disegna la tangente che attraversa il punto (-6, -1).
-
2Calcola la derivata prima per trovare l'equazione della "pendenza" della retta tangente. Per la funzione f(x), la derivata prima f'(x) rappresenta l'equazione della pendenza della retta tangente in qualsiasi punto di f(x). Esistono molti modi per calcolare la derivata. Eccone uno semplice, che sfrutta la regola delle potenze:[1]
-
Esempio 1 (cont.): il grafico è descritto dalla funzione .
Per calcolare la derivata, ricorda la regola delle potenze: .
La derivata prima della funzione = f'(x) = (2)(0,5)x + 3 - 0.
f'(x) = x + 3. Inserisci qualsiasi valore di x all'interno dell'equazione e il risultato sarà la pendenza della retta tangente a f(x) nel punto in cui x = a.
-
Esempio 1 (cont.): il grafico è descritto dalla funzione .
-
3Inserisci il valore di x del punto che hai preso in esame. Leggi il problema per scoprire le coordinate del punto di cui vuoi trovare la tangente. Inserisci la coordinata x di quel punto in f'(x). Il risultato sarà la pendenza della retta tangente in quel punto.
-
Esempio 1 (cont.): il punto indicato dal problema è (-6, -1). Usa la coordinata x -6 come valore per f'(x):
f'(-6) = -6 + 3 = -3
La pendenza della retta tangente è -3.
-
Esempio 1 (cont.): il punto indicato dal problema è (-6, -1). Usa la coordinata x -6 come valore per f'(x):
-
4Scrivi l'equazione della retta tangente nella forma , in cui m è la pendenza e è un punto della linea.[2] Ora hai tutte le informazioni necessarie per scrivere l'equazione della retta tangente in questa forma.
-
Esempio 1 (cont.):
La pendenza della retta è -3, quindi
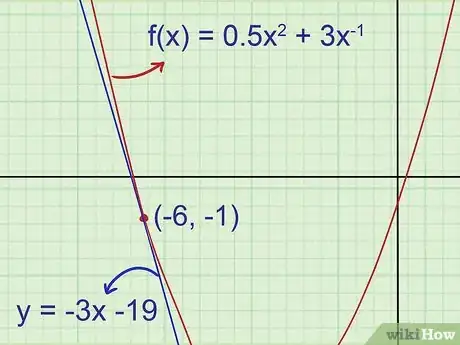
La retta tangente passa attraverso (-6, -1), quindi l'equazione finale è
Semplifica per ottenere
.
-
Esempio 1 (cont.):
-
5Conferma l'equazione sul tuo grafico. Se hai una calcolatrice grafica, disegna la funzione originale e la retta tangente, in modo da verificare che la tua risposta sia corretta. Se stai lavorando su carta, fai riferimento al grafico che hai tracciato in precedenza e assicurati che non siano presenti errori evidenti.
- Esempio 1 (cont.): il primo disegno mostrava che la pendenza della retta tangente era negativa e che l'intercetta verticale si trovava ben al di sotto del punto -5.5. L'equazione della retta tangente che abbiamo calcolato è y = -3x - 19, quindi -3 è la pendenza e -19 l'intercetta verticale. Entrambi questi valori corrispondono alle previsioni iniziali.
-
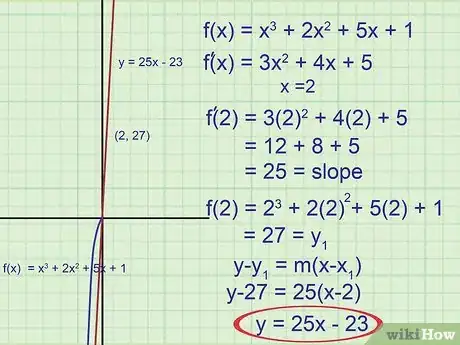
6Prova un problema più difficile. Ecco un riassunto dell'intero procedimento. Questa volta, l'obiettivo è trovare la retta tangente alla curva nel punto x = 2:
- Utilizzando la regola delle potenze, la derivata prima è . Questa funzione indica la pendenza della tangente.
- Dato che x = 2, calcola . Hai ottenuto il valore della pendenza nel punto x = 2.
- Nota che non abbiamo un punto questa volta, solo la coordinata x. Per trovare la coordinata y, sostituisci x = 2 nella funzione iniziale: . Il punto preso in esame è (2,27).
- Scrivi l'equazione della retta tangente nella forma:
Se necessario, semplifica in y = 25x - 23.
Pubblicità
Risolvere Problemi Correlati
-
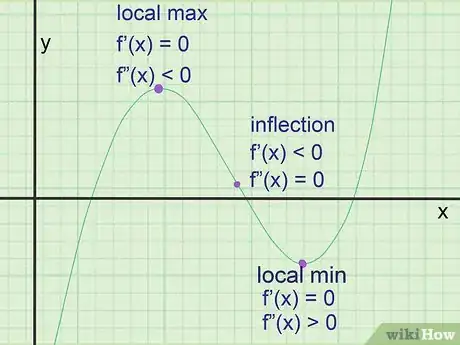
1Trova i punti estremi di un grafico. Si tratta dei punti in cui la funzione raggiunge un massimo locale (un punto più alto rispetto a quelli immediatamente adiacenti) o un minimo locale (un punto più basso di quelli immediatamente adiacenti). La retta tangente ha sempre pendenza pari a 0 in questi punti (una linea orizzontale), ma questo fattore da solo non basta a garantire la presenza di un estremo. Ecco come trovarli:[3]
- Calcola la derivata prima della funzione per ottenere f'(x), l'equazione della pendenza della retta tangente.
- Risolvi per f'(x) = 0, in modo da trovare i possibili estremi.
- Calcola la derivata seconda f''(x), l'equazione che indica la rapidità della variazione della pendenza della retta tangente.
- Per ciascun estremo possibile, inserisci la coordinata x a in f''(x). Se f''(a) è positivo, in a si trova un minimo locale. Se f''(a) è negativo, hai trovato un massimo locale. Se f''(a) = 0, quel punto indica un'inflessione e non è un estremo.
- Se nel punto a sono presenti un massimo o un minimo, calcola f(a) per conoscere la coordinata y.
-
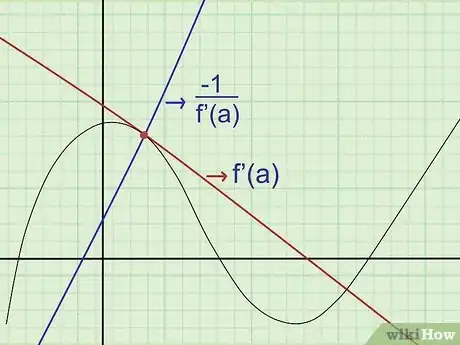
2Trova l'equazione della normale. La "normale" a una curva in un punto attraversa quel punto e ha pendenza perpendicolare alla tangente. Per conoscere la sua equazione, sfrutta il fatto che (pendenza della tangente)(pendenza della normale) = -1, quando passano per lo stesso punto del grafico.[4] In altre parole:
- Calcola f'(x), la pendenza della retta tangente.
- Se il punto si trova in x = a, calcola f'(a) per conoscere la pendenza della tangente in quel punto.
- Calcola per trovare la pendenza della normale.
- Scrivi l'equazione della retta normale.
Pubblicità
Consigli
- Se necessario, inizia riscrivendo l'equazione iniziale nella forma classica: f(x) = ... o y = ...
Riferimenti
- ↑ https://www.mathsisfun.com/calculus/derivatives-rules.html
- ↑ http://gato-docs.its.txstate.edu/jcr:48ee831e-5969-4419-b9f8-820925a1b46a/Finding%20the%20Equation%20of%20a%20Tangent%20Line.pdf
- ↑ http://www.themathpage.com/acalc/max.htm
- ↑ http://revisionmaths.com/advanced-level-maths-revision/pure-maths/calculus/tangents-and-normals



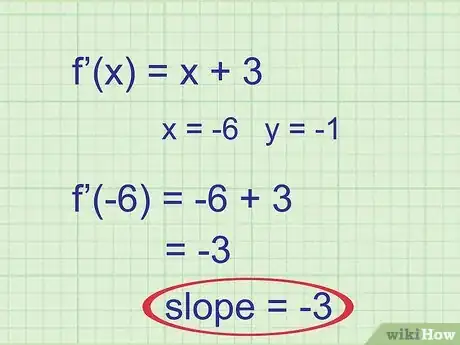
















-to-Grams-(g)-Step-12-Version-4.webp)














-to-Grams-(g)-Step-12-Version-4.webp)
