wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 19 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Ci sono 13 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 28 492 volte
La circonferenza di un cerchio è l'insieme dei punti equidistanti dal suo centro che ne delimitano l'area. Se un cerchio presenta una circonferenza di 3 km, significa che dovrai camminare per tale distanza, lungo tutto il perimetro del cerchio, prima di poter fare ritorno al punto di partenza. Quando sei alle prese con problemi di geometria, per trovare la soluzione non avrai la necessità di uscire di casa per sperimentare fisicamente. Per prima cosa leggi con molta attenzione il testo del problema per individuare i dati fondamentali di un cerchio, come il raggio (r), il diametro (d) o l'area (A), quindi fai riferimento alla sezione dell'articolo adatta per trovare la soluzione al tuo problema specifico. All'interno di questa guida vengono fornite anche le istruzioni per poter misurare fisicamente la circonferenza di un oggetto circolare.
Passaggi
Calcolare la Circonferenza Usando il Raggio
-
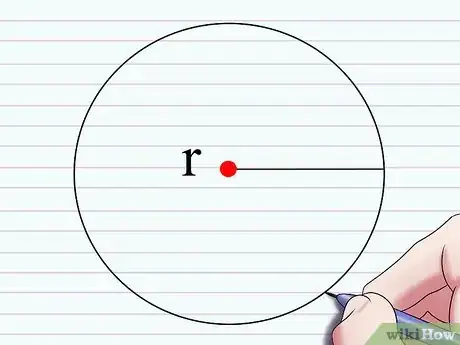
1Disegna il "raggio" di un cerchio. Traccia una linea che partendo dal centro raggiunga un punto qualsiasi della circonferenza del cerchio. Il segmento che hai disegnato rappresenta il "raggio" del tuo cerchio. Normalmente il raggio si indica con la lettera r all'interno delle equazioni e delle formule matematiche.[1]
- Nota: se il problema che devi risolvere non fornisce la lunghezza del raggio, dovrai fare riferimento a una delle altre sezioni dell'articolo. In questo caso dovrai usare il diametro o l'area per poter risalire alla lunghezza della circonferenza.
-
2Disegna il "diametro" del cerchio.[2] Prolunga il segmento che indica il raggio in modo che passando dal centro raggiunga l'estremità opposta della circonferenza. In altre parole hai disegnato un secondo raggio. Questi due raggi uniti rappresentano il "diametro" del cerchio, che normalmente è indicato con la lettera d. A questo punto avrai anche capito il motivo per cui puoi calcolare la misura del diametro di un cerchio partendo dal raggio e viceversa, dato che il primo misura esattamente il doppio del secondo, cioè d = 2r.
-
3Comprendi il significato della costante π ("pi greco").[3] Il simbolo π, che fa riferimento alla lettera greca pi, non rappresenta un numero magico che casualmente funziona per i problemi di geometria; in realtà il π è stato "scoperto" proprio misurando la circonferenza dei cerchi. Se si prova a misurare la circonferenza di qualsiasi cerchio (per esempio usando un metro) e la si divide per la lunghezza del diametro, si otterrà sempre il medesimo risultato, cioè il valore della costante pi greco. Si tratta di un numero molto particolare perché non può essere riportato sotto forma di semplice frazione o di un numero decimale, dato che ha un numero infinito di cifre. Tuttavia, come regola generale, si usa la sua forma arrotondata, che tutti sappiamo essere pari a 3,14.[4]
- Anche il valore della costante π memorizzata nelle calcolatrici non usa il numero reale, sebbene ne usi uno che ci si avvicina molto.
-
4Prendi nota della definizione matematica della costante π. Come spiegato in precedenza, la costante π indica il rapporto esistente fra la circonferenza di un cerchio e il suo diametro. Riportando questa definizione in termini matematici otterrai la seguente equazione: π = C / d. Dato che sai che il diametro di un qualsiasi cerchio è pari al doppio del raggio, cioè 2r, la formula appena ottenuta può essere riscritta nel seguente modo: π = C / 2r.
- C è la variabile che indica la "circonferenza" di un cerchio.[5]
-
5Risolvi l'equazione ottenuta nel passaggio precedente in base a C per trovare la circonferenza di un cerchio. Dato che il tuo scopo è quello di calcolare la lunghezza della circonferenza di un cerchio, devi risolvere l'equazione data in base alla variabile C. Moltiplicando entrambi i membri dell'equazione per 2r otterrai π x 2r = (C / 2r) x 2r, che semplificando è come scrivere 2πr = C.[6]
- Il membro sinistro della formula può anche essere indicato nella forma π2r; è comunque corretto. Normalmente i numeri vengono indicati prima delle variabili all'interno delle formule, in modo che le equazioni risultino più semplici da leggere e comprendere. Questo passaggio non cambia il risultato finale dell'equazione.
- Nelle equazioni matematiche è sempre possibile moltiplicare entrambi i membri per il medesimo valore e ottenere un'equazione equivalente.
-
6Sostituisci le variabili della formula con i numeri reali ed esegui i calcoli per trovare il valore di C. Adesso che sai che la circonferenza di un cerchio può essere calcolata usando la formula 2πr = C, fai riferimento al testo originale del tuo problema di geometria per risalire al valore di r (cioè il raggio del cerchio che stai studiando). Sostituisci la costante π con il valore 3,14 oppure usa una calcolatrice scientifica che sia dotata del tasto "π" per ottenere un risultato più preciso. Risolvi l'espressione "2πr" utilizzando i numeri che hai individuato (3,14 e la lunghezza del raggio). Il risultato che otterrai sarà pari alla circonferenza del cerchio in oggetto.
- Per esempio, se il raggio del cerchio che stai osservando è pari a 2 unità, otterrai 2πr = 2 x (3,14) x (2 unità) = 12,56 unità. In questo esempio la circonferenza sarà pari a 12,56 unità.
- Risolvendo il medesimo problema di esempio usando una calcolatrice scientifica dotata di tasto "π", otterrai un risultato più preciso: 2 x π x 2 unità = 12,56637. Tuttavia, se il tuo professore non ti ha fornito istruzioni diverse, potrai arrotondare il risultato ottenuto a 12,57 unità.
Pubblicità
Calcolare la Circonferenza Usando il Diametro
-
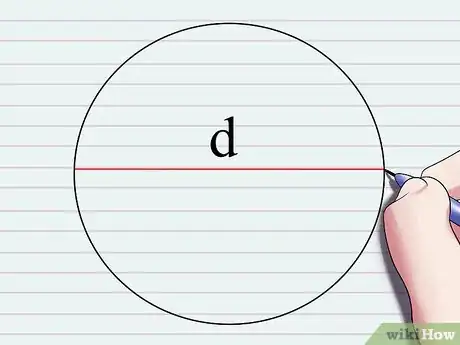
1Comprendi il significato di "diametro". Appoggia la punta di una matita su un foglio di carta dove hai precedentemente disegnato un cerchio. Allinea la punta con la circonferenza di quest'ultimo. Adesso traccia una linea che, passando per il centro del cerchio, raggiunga il punto opposto della circonferenza. Il segmento che hai appena tracciato rappresenta il "diametro" del cerchio in esame, che viene normalmente indicato con la variabile d all'interno dei problemi di matematica e geometria.[7]
- La linea che hai disegnato deve passare esattamente per il centro del cerchio, altrimenti non rappresenterà il suo diametro.
- Nota: se il problema che devi risolvere non fornisce la lunghezza del diametro, dovrai fare riferimento a una delle altre sezioni dell'articolo per poter risalire alla lunghezza della circonferenza.
-
2Comprendi il significato della seguente equazione d = 2r. Il "raggio" di un cerchio, indicato normalmente dalla variabile r, rappresenta la distanza che separa il centro da un punto qualsiasi della circonferenza.[8] Dato che il diametro è il segmento che unisce due punti opposti della circonferenza passando dal centro, si intuisce facilmente che la sua lunghezza è pari al doppio del raggio. In altre parole è sempre vera la seguente equazione: d = 2r. Questo significa che, all'interno di una equazione o di una formula, puoi sempre sostituire la variabile d con 2r o viceversa.
- In questo caso userai la variabile d e non la forma 2r, dato che il problema che dovrai affrontare ti fornirà la lunghezza del diametro d e non quella del raggio. Tuttavia, è molto importante comprendere il significato di questo passaggio, in modo da non confonderti se il tuo professore o il libro di matematica fanno riferimento al diametro d con il valore 2r.
-
3Comprendi il significato della costante π ("pi greco").[9] Il simbolo π, che fa riferimento alla lettera greca pi, non rappresenta un numero magico che casualmente funziona per i problemi di geometria. In realtà il π è stato "scoperto" proprio misurando la circonferenza dei cerchi. Se si prova a misurare la circonferenza di qualsiasi cerchio (per esempio usando un metro) e la si divide per la lunghezza del diametro, si otterrà sempre il medesimo risultato, cioè il valore della costante pi greco. Si tratta di un numero molto particolare perché non può essere riportato sotto forma di semplice frazione o di un numero decimale, dato che ha un numero infinito di cifre. Tuttavia, come regola generale, si usa la sua forma arrotondata che tutti sappiamo essere pari a 3,14.[10]
- Anche il valore della costante π memorizzata nelle calcolatrici non usa il numero reale, sebbene ne usi uno che ci si avvicina molto.
-
4Prendi nota della definizione matematica della costante π. Come spiegato in precedenza, la costante π indica il rapporto esistente fra la circonferenza di un cerchio e il suo diametro. Riportando questa definizione in termini matematici otterrai la seguente equazione: π = C / d.
-
5Risolvi l'equazione fornita nel passaggio precedente, in base alla variabile C, per calcolare la circonferenza. Dato che vuoi calcolare la lunghezza della circonferenza di un cerchio, dovrai modificare la formula in esame in modo che la variabile C risulti isolata in un membro dell'equazione. Per ottenere tale risultato, moltiplica entrambi i membri della formula per d:
- π x d = (C / d) x d;
- πd = C.
-
6Sostituisci le variabili della formula con i numeri reali ed esegui i calcoli per trovare il valore di C. Fai riferimento al testo originale del tuo problema per risalire al valore del diametro d e sostituiscilo all'interno dell'equazione che hai ottenuto nel passaggio precedente. Sostituisci la costante π con il valore 3,14 oppure usa una calcolatrice scientifica che sia dotata del tasto "π" per ottenere un risultato più preciso. Moltiplica i valori di π e d per ottenere il valore di C, la lunghezza della circonferenza del cerchio in oggetto.[11]
- Per esempio, se il diametro del cerchio che stai osservando è pari a 6 unità, otterrai 2πd = (3,14) x (6 unità) = 18,84 unità. In questo esempio la circonferenza sarà pari a 18,84 unità.
- Risolvendo il medesimo problema di esempio usando una calcolatrice scientifica dotata di tasto "π", otterrai un risultato più preciso: π x 6 unità = 18,84956. Tuttavia, se il tuo professore non ti ha fornito istruzioni diverse, potrai arrotondare il risultato ottenuto a 18,85 unità.
Pubblicità
Calcolare la Circonferenza Usando l'Area
-
1Comprendi come si calcola l'area di un cerchio. Nella maggior parte dei casi non si misura fisicamente l'area (A) di un cerchio. Normalmente occorre misurare semplicemente il raggio (r) e poi risalire all'area corrispondente usando la seguente formula matematica: A = πr2. La dimostrazione matematica della correttezza di questa formula risulta un po' complicata, ma se sei interessato puoi avere maggiori informazioni leggendo questo articolo.[12]
- Nota: se il problema che devi risolvere non fornisce il valore dell'area, dovrai fare riferimento a una delle altre sezioni dell'articolo per poter risalire alla lunghezza della circonferenza.
-
2Scopri la formula per calcolare la circonferenza di un cerchio. La circonferenza (C) di un cerchio è l'insieme dei punti equidistanti dal suo centro che ne delimitano l'area. Normalmente puoi calcolarla usando la formula C = 2πr. Tuttavia, dato che in questo caso non conosci direttamente il valore del raggio (r), dovrai spendere un po' di tempo nel calcolarne il valore.[13]
-
3Risali alla formula che ti permetterà di calcolare il raggio di un cerchio a partire dalla sua area. Dato che l'area di un cerchio è definita dalla formula A = πr2, puoi risalire alla formula inversa risolvendo l'equazione in base alla variabile r. Se i passaggi indicati di seguito ti appaiono troppo complessi, prova a iniziare da problemi di algebra più semplici oppure approfondisci la tua conoscenza dell'algebra.
- A = πr2;
- A / π = πr2 / π = r2;
- √(A/π) = √(r2) = r;
- r = √(A/π).
-
4Modifica la formula iniziale per calcolare la circonferenza usando l'equazione che hai ottenuto nel passaggio precedente. Quando affronti una qualsiasi equazione, per esempio r = √(A/π), sappi che puoi sostituire un membro con una forma corrispondente. Usa questa tecnica per modificare correttamente la formula iniziale della circonferenza C = 2πr. In questo caso non conosci direttamente il valore della variabile "r", però conosci il valore dell'area, "A". Sostituisci la variabile "r" con la formula che hai ricavato nel passaggio precedente, in modo da poter effettuare i calcoli:
- C = 2πr;
- C = 2π(√(A/π)).
-
5Sostituisci le variabili della formula con i valori noti, per poter risalire alla circonferenza. Usa il valore dell'area che ti è stato fornito nel testo del problema ed effettua i calcoli per ottenere il risultato finale. Per esempio, se l'area (A) del cerchio in esame è pari a 15 unità quadrate, risolvi il seguente calcolo 2π(√(15/π)) usando una calcolatrice. Ricorda di inserire anche le parentesi tonde nella formula, altrimenti il risultato non sarà corretto.[14]
- Il risultato che otterrai dal problema di esempio sarà 13,72937. Tuttavia, se il tuo professore non ti ha fornito istruzioni diverse potrai arrotondare il risultato ottenuto a 13,73 unità quadrate.
Pubblicità
Misurare la Circonferenza di un Cerchio Reale
-
1Usa questo metodo se hai la necessità di misurare fisicamente degli oggetti circolari reali. Ricorda che è possibile risalire alla circonferenza anche di oggetti presenti nel mondo reale, non solo di quelli descritti nei problemi di matematica e geometria. Prova a misurare la circonferenza di una ruota della tua bicicletta, di una pizza o di una moneta.
-
2Procurati un pezzo di corda o filo e un righello. La corda dovrà essere sufficientemente lunga per poter essere avvolta intorno alla circonferenza dell'oggetto. Inoltre, dovrà anche essere molto flessibile in modo da poter essere avvolta saldamente intorno all'oggetto. A questo punto ti serve uno strumento con cui poter effettuare la misurazione, per esempio un metro a nastro o un righello. Eseguire la misurazione risulterà più facile se il righello o il metro è più lungo del pezzo di corda da misurare.[15]
-
3Avvolgi la corda intorno all'oggetto solo una volta.[16] Inizia appoggiando un'estremità della corda su un lato dell'oggetto da misurare. A questo punto avvolgila tutta intorno alla circonferenza, assicurandoti che risulti il più tesa possibile. Se devi misurare una moneta o un oggetto molto sottile, potresti non essere in grado di tendere correttamente la corda o il filo lungo la circonferenza. Appoggia l'oggetto da misurare su una superficie piana, quindi avvolgi la corda intorno alla base cercando di tenderla il più possibile.
- Fai attenzione a non sovrapporre le estremità della corda o del filo. Dovrai avvolgere l'oggetto solo una volta, altrimenti la misurazione sarà falsata. Al termine di questo passaggio, dovresti avere un singolo anello di corda che in nessuna sezione dovrà risultare doppio.
-
4Marca o taglia la corda. Individua il punto in cui il cerchio di corda si chiude, cioè ritorna al punto iniziale. Adesso segna il punto in esame con un pennarello o una penna oppure usa un paio di forbici per recidere il tratto di corda che descrive perfettamente la circonferenza dell'oggetto da misurare.
-
5Adesso distendi la corda e misurane la lunghezza usando un righello o un metro. Se hai scelto di usare un pennarello, dovrai misurare il pezzo di corda che va dal punto iniziale fino al segno che hai tracciato. Si tratta del pezzo di corda che avvolgeva interamente la circonferenza dell'oggetto e che ti darà la risposta che stai cercando. La lunghezza del tratto di corda in esame è equivalente alla circonferenza dell'oggetto.[17]Pubblicità
Consigli
- Ricorda di riportare il risultato finale dei tuoi calcoli usando sempre le unità di misura corrette.[18]
Riferimenti
- ↑ https://www.mathopenref.com/radius.html
- ↑ https://www.mathsisfun.com/geometry/circle.html
- ↑ https://www.livescience.com/29197-what-is-pi.html
- ↑ https://www.mathsisfun.com/numbers/pi.html
- ↑ https://www.mathexpression.com/circumference-of-a-circle.html
- ↑ https://www.aaamath.com/geo612x4.htm
- ↑ https://www.mathsisfun.com/definitions/diameter.html
- ↑ https://www.mathopenref.com/radius.html
- ↑ https://www.livescience.com/29197-what-is-pi.html
- ↑ https://www.mathsisfun.com/numbers/pi.html
- ↑ https://www.piday.org/calculators/circumference-calculator/
- ↑ https://www.mathsisfun.com/geometry/circle-area.html
- ↑ https://www.mathplanet.com/education/pre-algebra/more-about-equation-and-inequalities/calculating-the-circumference-of-a-circle
- ↑ https://www.khanacademy.org/math/basic-geo/basic-geo-area-and-perimeter/area-circumference-circle/v/circumference-from-area
- ↑ https://www.eduplace.com/math/mw/background/6/10/te_6_10_area_ideas.html
- ↑ https://www.eduplace.com/math/mw/background/6/10/te_6_10_area_ideas.html
- ↑ https://www.eduplace.com/math/mw/background/6/10/te_6_10_area_ideas.html
- ↑ http://www.merriam-webster.com/dictionary/radius

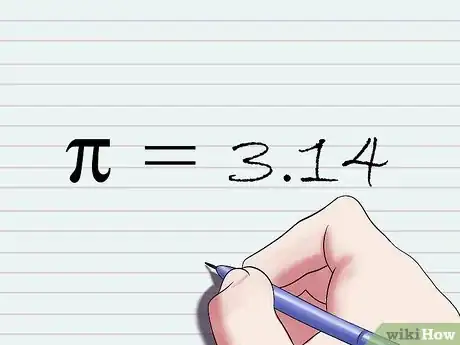
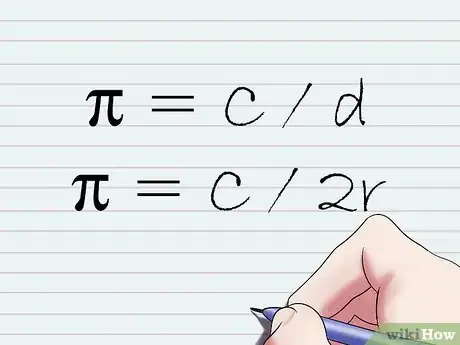
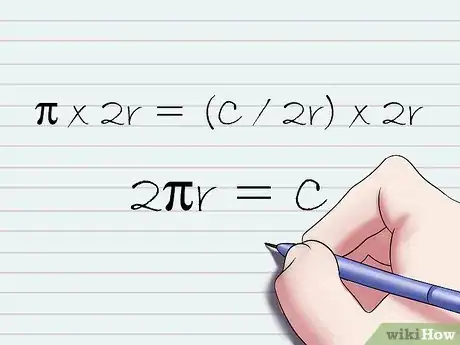
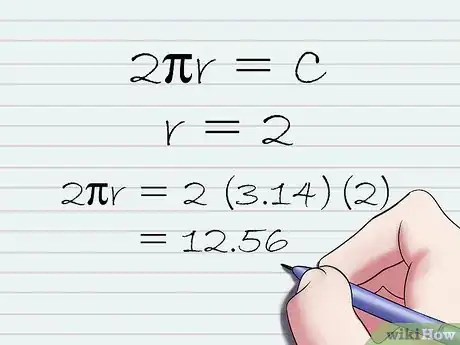
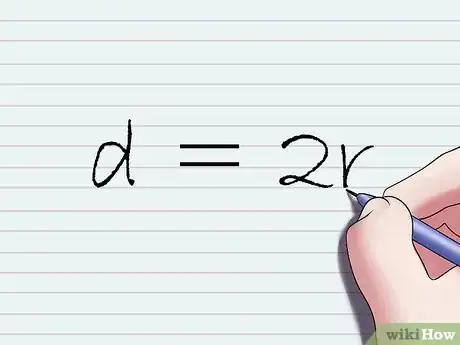
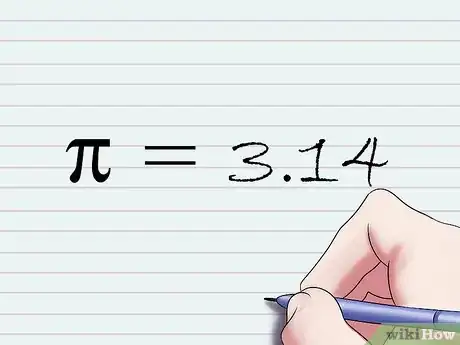
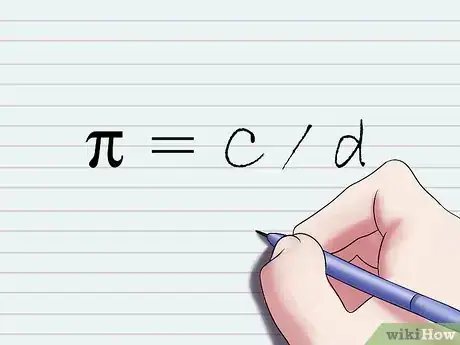
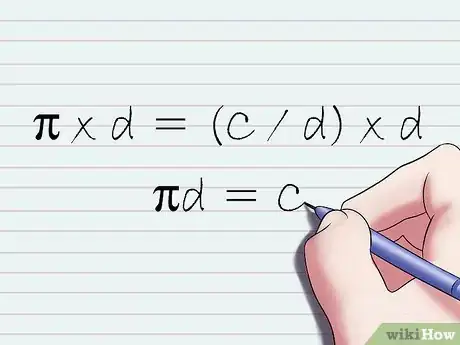
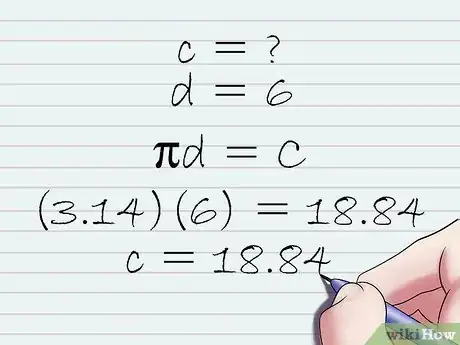
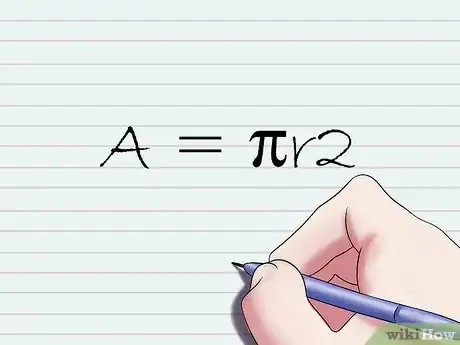
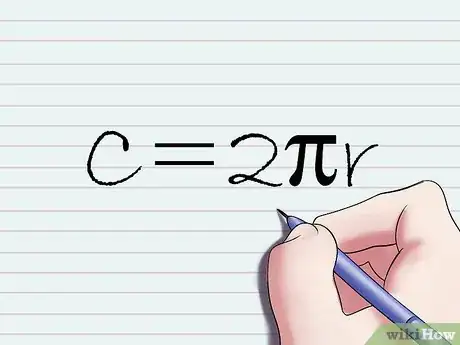
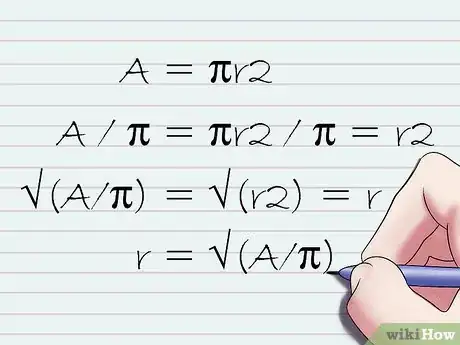
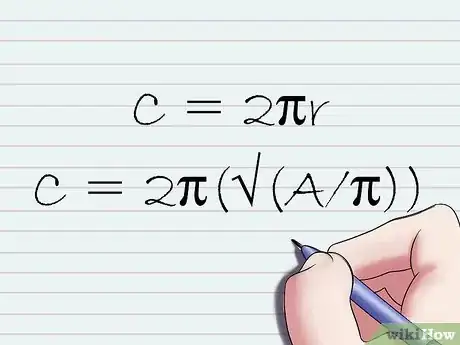
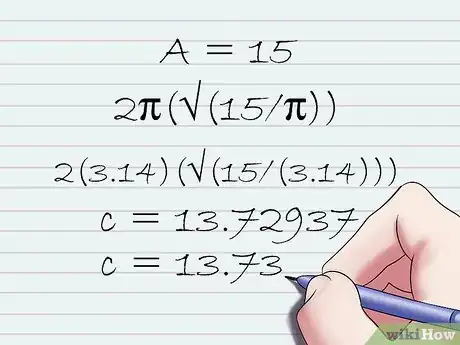








-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
