X
wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 31 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Questo articolo è stato visualizzato 21 168 volte
Prima dei computer e delle calcolatrici, i logaritmi venivano calcolati velocemente usando le tavole logaritmiche. Queste tavole possono ancora essere utili per calcolarli rapidamente o moltiplicare grandi numeri, una volta che hai capito come usarle.
Passaggi
Metodo 1
Metodo 1 di 3:
Leggere una Tavola Logaritmica
-
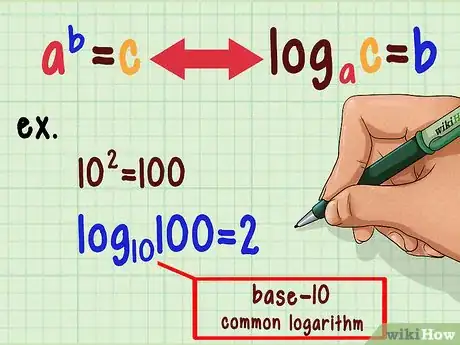
1Impara la definizione di logaritmo. 102 = 100. 103 = 1000. Le potenze 2 e 3 sono i logaritmi in base 10, di 100 e 1000.[1] In generale, ab = c può essere riscritto come logac = b. Quindi, dire "dieci elevato due fa 100" è equivalente a dire "il logaritmo in base 10 di 100 è due". Le tavole logaritmiche sono in base 10, quindi a deve sempre essere 10.
- Moltiplica due numeri addizionando le loro potenze. Ad esempio: 102 * 103 = 105, o 100 * 1000 = 100,000.
- Il logaritmo naturale, rappresentato con "ln", è il logaritmo in base "e", dove "e" è la costante 2,718. È un numero molto utilizzato in diverse aree della matematica e della fisica. Puoi usare delle tavole relative al logaritmo naturale nello stesso modo che usi quelle in base 10.
-
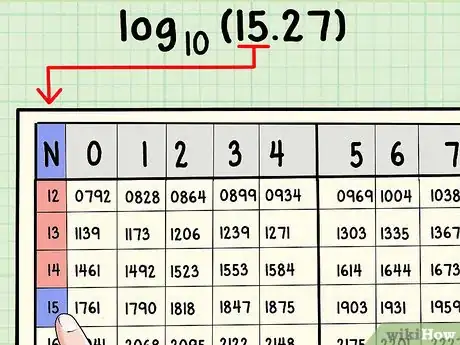
2Identifica la caratteristica del numero di cui vuoi trovare il logaritmo naturale. 15 sta fra 10 (101) e 100 (102), quindi il suo logaritmo sarà compreso fra 1 e 2, e sarà quindi "1,qualcosa". 150 sta fra 100 (102) e 1000 (103), quindi il suo logaritmo sarà compreso tra 2 e 3, e sarà "2,qualcosa". Quel ",qualcosa" è detto mantissa; questo è ciò che trovi nella tavola logaritmica. Ciò che sta prima del punto decimale (1 nel primo esempio, 2 nel secondo) è la caratteristica.
-
3Scorri il tuo dito sulla riga giusta utilizzando la colonna più a sinistra. Questa colonna mostrerà le prime due cifre decimali del numero che stai cercando — per qualche tavola più grande anche tre. Se vuoi trovare il logaritmo di 15,27 in una tavola in base 10, vai sulla riga contenente 15. Se vuoi trovare il logaritmo di 2,577, vai sulla riga contenente 25.
- In alcuni casi i numeri nella riga avranno dei punti decimali, cercherai quindi 2,5 piuttosto che 25. Puoi ignorare questo punto decimale, dato che non influirà sul risultato.
- Ignora anche ogni cifra decimale del numero per cui stai cercando il logaritmo, dato che la mantissa del logaritmo di 1,527 non è differente da quella di 152,7.
-
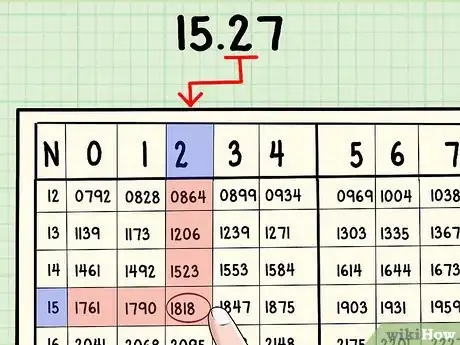
4Nella riga appropriata, fai scorrere il tuo dito sulla colonna corretta. Questa colonna sarà quella avente per intestazione la prima delle cifre decimali del numero. Ad esempio, se vuoi trovare il logaritmo di 15,27, il tuo dito sarà sulla riga con 15. Scorri il tuo dito fino alla colonna 2. Starai puntando al numero 1818. Prendine nota.
-
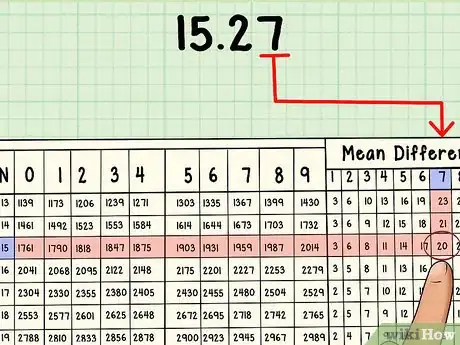
5Se la tua tavola possiede anche le differenze tabulari, scorri il tuo dito fra le colonne fino a giungere a quella voluta. Per 15,27, il numero è 7. Il tuo dito si trova attualmente sulla riga 15 e colonna 2. Scorri alla riga 15 e alla differenza tabulare 7. Starai puntando al numero 20. Annotalo.
-
6Somma i numeri ottenuti nei due passaggi precedenti. Per 15,27, otterrai 1838. È la mantissa del logaritmo di 15,27.
-
7Somma la caratteristica. Dato che 15 è compreso fra 10 e 100 (101 e 102), il log di 15 deve essere compreso fra 1 e 2, quindi "1,qualcosa", quindi la caratteristica è 1. Combina la caratteristica con la mantissa. Troverai che il log di 15,27 è 1,1838.Pubblicità
Metodo 2
Metodo 2 di 3:
Trovare l'Anti-Log
-
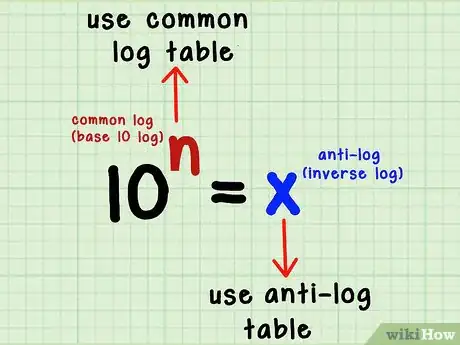
1Capire la tavola anti-log. Usa questa tavola quando conosci il logaritmo di un numero, ma non il numero stesso. Nella formula 10n = x, n è il logaritmo, in base 10, di x. Se hai x, trovi n usando le tavole logaritmiche. Se hai n, trova x usando la tavola anti-log.
- L'anti-log è anche conosciuto come logaritmo inverso.
-
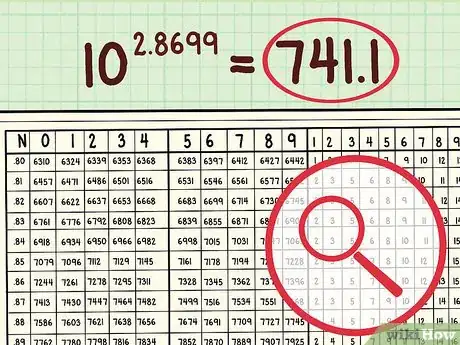
2Scrivi la caratteristica. È il numero prima del punto decimale. Se stai cercando l'anti-log di 2,8699, la caratteristica è 2. Rimuovila momentaneamente dal numero che stai guardando, ma assicurati di scriverla per non dimenticarla – sarà importante più avanti.
-
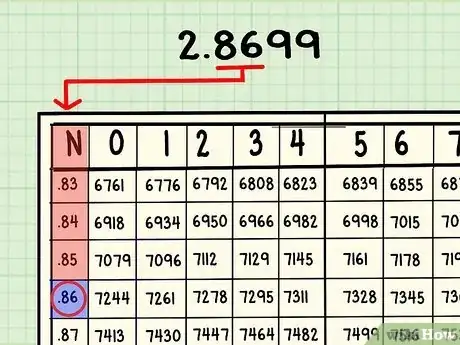
3Trova la riga che corrisponde alla prima parte della mantissa. In 2,8699, la mantissa è ",8699". La maggior parte delle tavole inverse, come molte delle tavole logaritmiche, ha due numeri nella colonna più a sinistra, quindi scorri in basso con il dito fino a ",86".
-
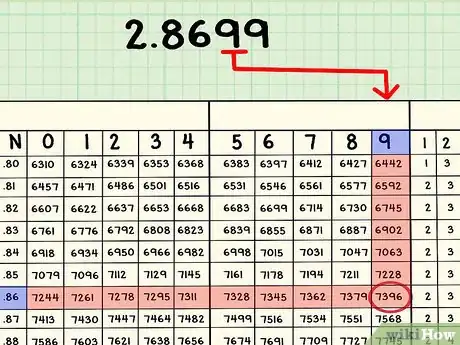
4Scorri fino alla colonna contenente il numero successivo della mantissa. Per 2,8699, scorri fino alla riga con ",86" e trova l'intersezione con la colonna 9. Dovrebbe esserci 7396. Annotalo.
-
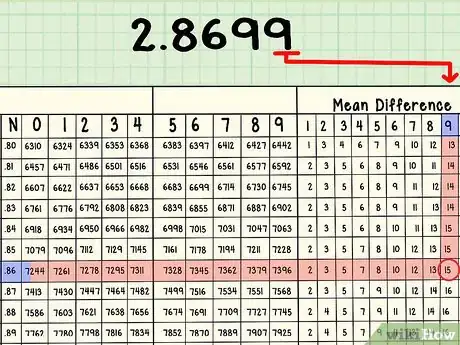
5Se la tua tavola possiede anche le differenze tabulari, scorri il dito sulla colonna finché non trovi la cifra successiva della mantissa. Assicurati di rimanere sulla stessa riga. In questo caso, scorrerai fino all'ultima colonna, la 9. L'intersezione della riga ",86" e della differenza tabulare 9 è 15. Prendine nota.
-
6Somma i due numeri dei passaggi precedenti. Nel nostro esempio, sono 7396 e 15. Sommali ottenendo 7411.
-
7Usa la caratteristica per posizionare il punto decimale. La nostra caratteristica era 2. Questo significa che la risposta è compresa fra 102 e 103, o fra 100 e 1000. Perché il numero 7411 stia fra 100 e 1000, il punto decimale deve andare dopo la terza cifra, in modo che il numero sia dell'ordine dei 700 anziché 70, che è troppo piccolo, o 7000, che è troppo grande. Quindi la risposta finale è 741,1.Pubblicità
Metodo 3
Metodo 3 di 3:
Moltiplicare i Numeri Usando le Tavole Logaritmiche
-
1Impara a moltiplicare i numeri usando i loro logaritmi. Sappiamo che 10 * 100 = 1000. Scritti in termini di potenze (o logaritmi), 101 * 102 = 103. Sappiamo anche che 1 + 2 = 3. In generale, 10x * 10y = 10x + y. Quindi la somma dei logaritmi di due numeri differenti è il logaritmo del prodotto di quei due numeri. Possiamo moltiplicare due numeri con la stessa base sommandone le potenze.
-
2Cerca i logaritmi dei due numeri che vuoi moltiplicare. Usa il metodo precedente per calcolarli. Ad esempio, se devi moltiplicare 15,27 e 48,54, devi trovare il log di 15,27 che è 1,1838 e il log di 48,54 che è 1,6861.
-
3Somma i due logaritmi per trovare il logaritmo della soluzione. In questo esempio, sommi 1,1838 e 1,6861 ottenendo 2,8699. Questo numero è il logaritmo della tua risposta.
-
4Controlla l'anti-logaritmo del risultato basandoti sul procedimento descritto nel passaggioo precedente. Puoi farlo trovando il numero nella tabella più vicino possibile alla mantissa di questo numero (8699). Il metodo più efficace è però utilizzare la tavola degli anti-log. In questo esempio, otterrai 741,1.Pubblicità
Consigli
- Fai sempre i calcoli su un foglio e non a mente, dato che questi numeri complicati possono trarti in inganno.
- Leggi l'intestazione della pagina con attenzione. Una tavola logaritmica ha circa 30 pagine e usare quella sbagliata ti porterà alla risposta sbagliata.
Pubblicità
Avvertenze
- Assicurati di effettuare le letture dalla stessa riga. In alcuni casi, potresti confonderti a causa della scrittura molto fitta.
- Usa i consigli forniti in questo articolo per il log in base 10, e assicurati che i numeri che stai utilizzando siano in formato decimale, o notazione scientifica.
- Molte tavole sono accurate solo fino alla terza o alla quarta cifra. Se trovi l'anti-log di 2,8699 usando una calcolatrice, la risposta si arrotonderà a 741,2, ma la risposta che ottieni usando le tavole logaritmiche sarà 741,1. Questo è dato agli arrotondamenti nelle tavole. Se ti serve una risposta più precisa, usa una calcolatrice o un altro metodo.
Pubblicità
Cose che ti Serviranno
- Tavole logaritmiche o libro contenente le tavole
- Foglio di carta bianco.
Riferimenti
Informazioni su questo wikiHow
Pubblicità



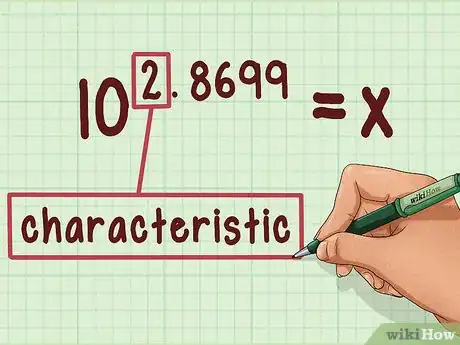
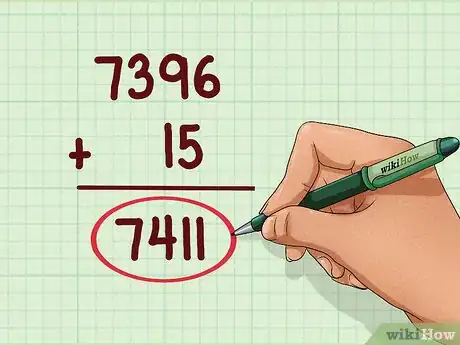
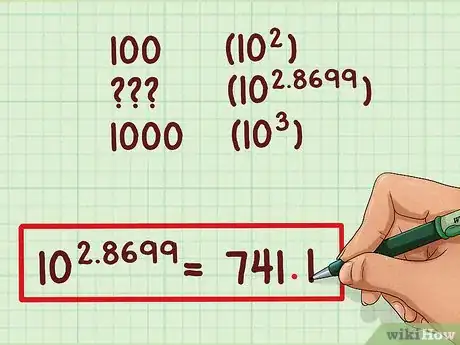
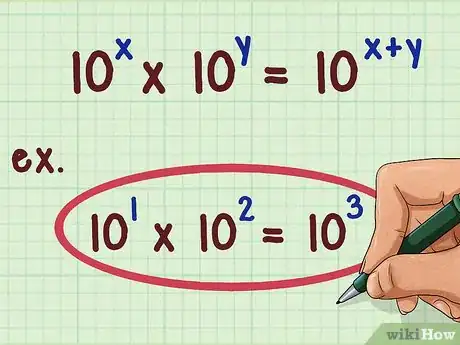

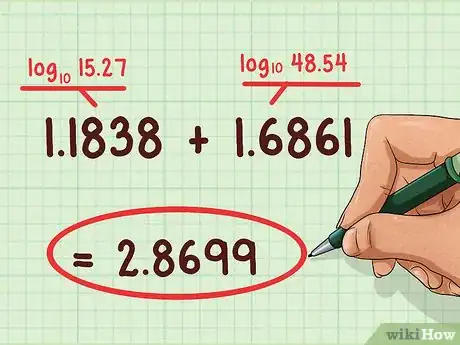



-to-Grams-(g)-Step-12-Version-4.webp)