wikiHow è una "wiki"; questo significa che molti dei nostri articoli sono il risultato della collaborazione di più autori. Per creare questo articolo, 24 persone, alcune in forma anonima, hanno collaborato apportando nel tempo delle modifiche per migliorarlo.
Ci sono 7 riferimenti citati in questo articolo, che puoi trovare in fondo alla pagina.
Questo articolo è stato visualizzato 6 736 volte
L'insieme di Mandelbrot è costituito da punti tracciati su un piano complesso in maniera da formare un frattale: un'impressionante figura geometrica dove ogni parte è una copia in miniatura dell'intero. Era possibile vedere le affascinanti immagini nascoste nell'insieme di Mandelbrot fin dal XVI secolo, grazie alla comprensione che aveva Rafael Bombelli dei numeri immaginari... ma fu solo dopo che Benoit Mandelbrot e altri iniziarono a esplorare i frattali con l'aiuto dei computer che questo universo segreto venne svelato.
Ora che sappiamo della sua esistenza, possiamo affrontarlo in un modo più “primitivo”: a mano! Ecco qui una maniera di visualizzare una rozza rappresentazione dell'insieme, con l'unico scopo di capire come viene realizzato; potrai quindi valutare meglio le rappresentazioni che puoi ottenere utilizzando i tanti programmi open source disponibili, o che puoi visualizzare su CD-ROM e DVD.
Passaggi
-
1Comprendi la formula di base, spesso espressa come z = z2 + c. Significa semplicemente che, per ogni punto nell'universo di Mandelbrot che vogliamo vedere, continuiamo a calcolare il valore di z finché non si verifica una delle due condizioni; poi lo coloriamo per mostrare quanti calcoli abbiamo fatto. Non preoccuparti! Diventerà tutto chiaro nei passaggi seguenti.
-
2Prendi tre matite, pastelli o pennarelli di colori differenti, oltre a una matita o una penna di colore nero per tracciare lo schema. La ragione per cui ci servono tre colori è che faremo una prima approssimazione con non più di tre iterazioni (o passaggi: in altre parole, applicando la formula fino a tre volte per ogni punto):
-
3Disegna con il pennarello nero una grande tabella per il tris di tre quadrati per tre, su un pezzo di carta.
-
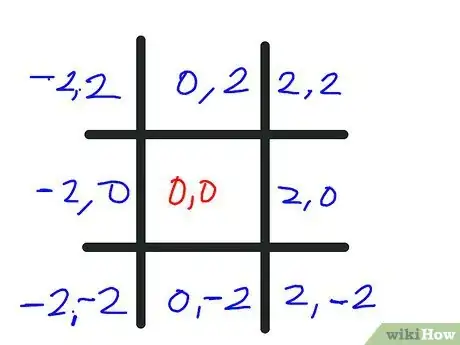
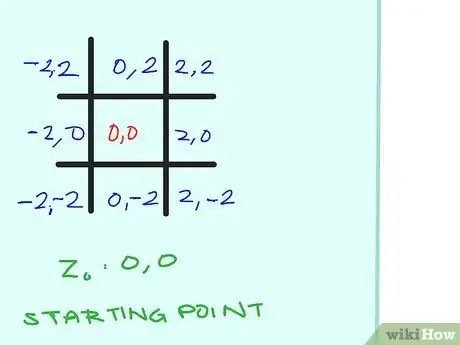
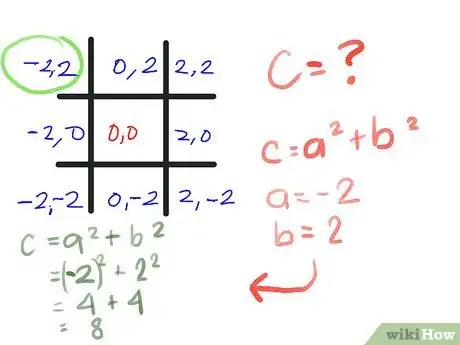
4Contrassegna (sempre in nero) il quadrato centrale (0,0). Questo è il valore costante (c) del punto nel centro esatto del quadrato. Diciamo ora che ogni quadrato è largo 2 unità, quindi somma e/o sottrai 2 ai/dai valori di x e y di ogni quadrato, essendo x e y rispettivamente il primo e il secondo numero. Fatto questo, il risultato sarà quello mostrato qui. Seguendo le celle orizzontalmente, i valori di y (il secondo numero) saranno invariati; seguendole invece verticalmente, lo saranno i valori di x (il primo numero).
-
5Calcola il primo passaggio, o iterazione, della formula. Come il computer (in effetti, il significato originario di questa parola è "persona che computa"), sei in grado di farlo da solo. Cominciamo da questi presupposti:
- Il valore di partenza di z di ogni quadrato è (0,0). Quando il valore assoluto di z per un dato punto è maggiore o uguale a 2, si dice che quel punto (e il suo quadrato corrispondente) è fuggito dall'insieme di Mandelbrot. In questo caso, colorerai il quadrato a seconda del numero di iterazioni della formula che hai applicato a quel punto.
- Scegli i colori che userai per i passaggi 1, 2 e 3. Supponiamo che, per gli scopi di questo articolo, siano rispettivamente il rosso, il verde e il blu.
- Calcola il valore di z per l'angolo superiore sinistro della tabella per il tris, supponendo un valore di partenza di z di 0+0i o (0,0) (vedi i Consigli per una comprensione migliore di queste rappresentazioni). Stiamo usando la formula z = z2 + c, come descritto nel primo passaggio. Ti accorgerai presto che, in questo caso, z2+c è semplicemente c, perché zero al quadrato è sempre zero. E cos'è c per questo quadrato? (-2,2).
- Determina il valore assoluto di questo punto; il valore assoluto di un numero complesso (a,b) è la radice quadrata di a2 + b2. Visto che lo confronteremo con il valore noto 2, possiamo evitare di calcolare le radici quadrate confrontando a2 + b2 con 22, che sappiamo equivale a 4. In questo calcolo, a = -2 e b = 2.
- ([-2]2 + 22) =
- (4 + 4) =
- 8, che è maggiore di 4.
- Dopo il primo calcolo è fuggito dall'insieme di Mandelbrot, perché il suo valore assoluto è maggiore di 2. Coloralo con la matita che hai scelto per il primo passaggio.
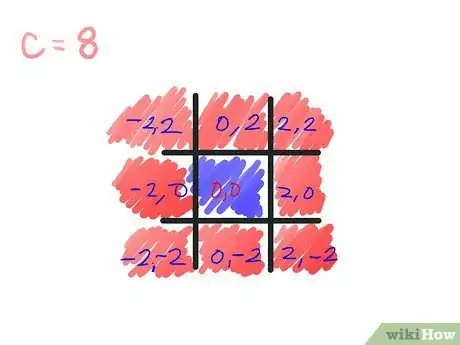
- Fai lo stesso per ogni quadrato della tabella, tranne che per quello centrale, che non fuggirà dall'insieme di Mandelbrot entro il terzo passaggio (né lo farà mai). Quindi hai usato solo due colori: quello del primo passaggio per tutti i quadrati esterni e quello del terzo passaggio per il quadrato centrale.
-
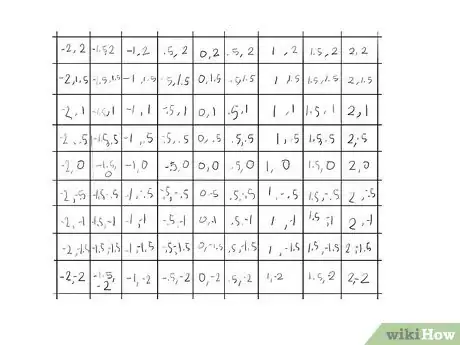
6Proviamo con un quadrato tre volte più grande, di 9 per 9, ma manteniamo un massimo di tre iterazioni.
-
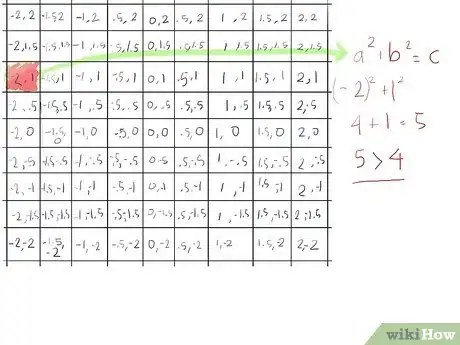
7Inizia con la terza fila dall'alto, perché è qui che la cosa diventa subito interessante.
- Il primo elemento (-2,1) è maggiore di 2 (perché (-2)2 + 12 risulta essere 5), quindi coloriamolo di rosso, visto che fugge dall'insieme di Mandelbrot al primo passaggio.
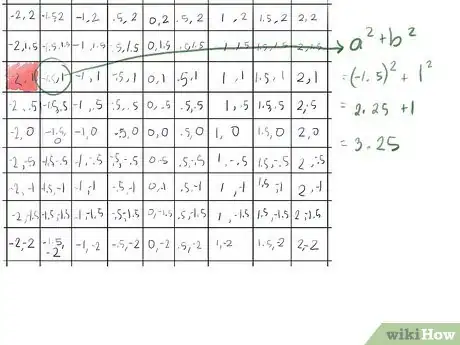
- Il secondo elemento (-1,5,1) risulta non maggiore di 2. Applicando la formula per il valore assoluto, x2+y2, con x = -1,5 e y = 1:
- (-1,5)2 = 2,.25
- 12 = 1
- 2,25 + 1 = 3,25, inferiore a 4, quindi la radice quadrata è inferiore a 2.
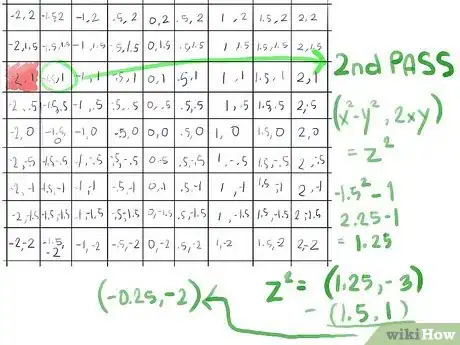
- Procediamo quindi col nostro secondo passaggio, calcolando z2+c attraverso la scorciatoia (x2-y2, 2xy) per z2 (vedi i Consigli per capire da dove si ricava questa scorciatoia), di nuovo con x = -1,5 e y = 1:
- (-1,5)2 - 12 diventa 2,25 - 1, che diventa ‘’’1,25;
- 2xy, dal momento che x è -1,5 e y è 1, diventa 2(-1,5), da cui risulta ‘’’-3,0’’’;
- Questo ci dà uno z2 di (1.25, -3)
- Ora aggiungi c per questa casella (somma x a x, y a y), ottenendo (-0,25,-2)
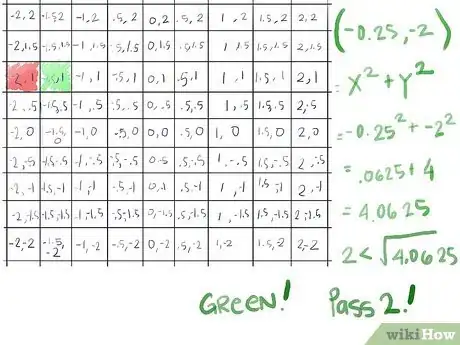
- Adesso controlliamo se il suo valore assoluto è maggiore di 2. Calcola x2 + y2:
- (-0,25)2 = 0,0625
- -22 = 4
- 0,0625 + 4 = 4,0625, la cui radice quadrata è maggiore di 2, perciò è fuggito dopo la seconda iterazione: il nostro primo verde!
- Quando avrai familiarizzato con i calcoli, a volte sarai in grado di riconoscere quali numeri fuggono dall'insieme di Mandelbrot con una semplice occhiata. In questo esempio, l'elemento y ha una grandezza di 2, che, dopo essere stato elevato al quadrato e sommato al quadrato dell'altro numero, sarà maggiore di 4. Qualunque numero maggiore di 4 avrà una radice quadrata maggiore di 2. Vedi i Consigli in basso per una spiegazione più dettagliata.
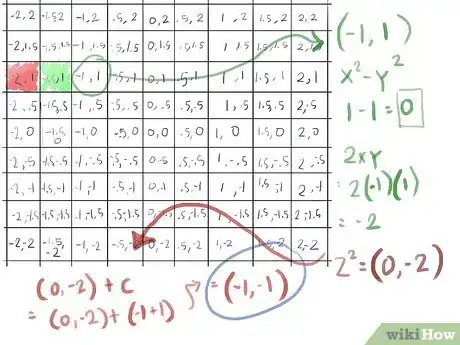
- Il terzo elemento, con c che ha valore di (-1,1), non fugge al primo passaggio: visto che sia 1 che -1, elevati al quadrato, sono sempre 1, x2+y2 è 2. Quindi calcoliamo z2+c, seguendo la scorciatoia (x2-y2, 2xy) per z2:
- (-1)2-12 diventa 1-1, che è 0;
- 2xy quindi è 2(-1) = -2;
- z2 = (0,-2)
- sommando c otteniamo (0,-2) + (-1,1) = (-1,-1)
- Questo è sempre lo stesso valore assoluto di prima (la radice quadrata di 2, circa 1,41); proseguendo con una terza iterazione:
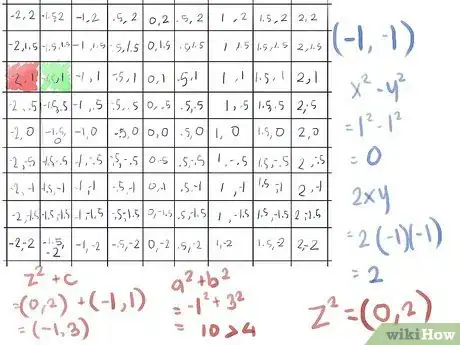
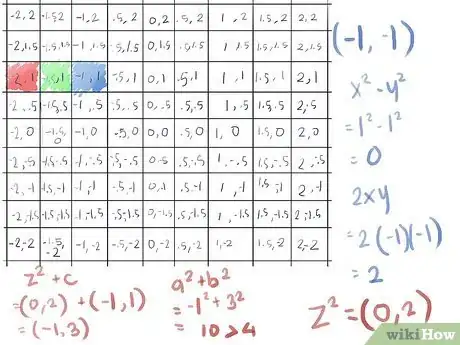
- ([-1]2)-([-1]2) diventa 1-1, che è 0 (di nuovo)...
- ma adesso 2xy è 2(-1)(-1), che è 2 positivo, che dà a z2 il valore di (0,2).
- sommando c otteniamo (0,2) + (-1,1) = (-1,3), che ha un a2 + b2 di 10, molto maggiore di 4.
- Perciò anche questo numero fugge. Colora la casella con il tuo terzo colore, il blu, e, visto che abbiamo completato tre iterazioni con questo punto, procedi alla successiva.
- Il limitarci all'uso di soli tre colori diventa qui chiaramente un problema, dal momento che qualcosa che fugge dopo tre sole iterazioni viene colorato come (0,0), che non fugge mai; ovviamente, a questo livello di dettaglio, non vedremo mai niente che si avvicini al "bug" di Mandelbrot.
-
8Continua a calcolare ogni casella finché non è fuggita o non hai raggiunto il numero massimo di iterazioni (il numero di colori che stai usando: tre, in questo esempio), livello al quale la colorerai. Ecco come si presenta la matrice di 9 per 9 dopo tre iterazioni in ogni quadrato... A quanto pare, stiamo scoprendo qualcosa!
-
9Ripeti la stessa matrice con altri colori (iterazioni) per mostrare i pochi livelli successivi, o, meglio ancora, disegna una matrice molto più grande per un progetto più a lungo termine! Puoi ottenere immagini più accurate:
- Aumentando il numero delle caselle; questa ne ha 81 per ogni lato. Nota la somiglianza con la matrice 9 per 9 in alto, ma anche i bordi più arrotondati del cerchio e dell'ovale.
- Aumentando il numero di colori (iterazioni); questa possiede 256 tonalità di rosso, verde e blu, per un totale di 768 colori invece di 3. Nota che in questo caso puoi vedere la linea del ben noto "lago" (o "bug", dipende da come lo consideri) di Mandelbrot. Lo svantaggio è la quantità di tempo che richiede; se riesci a calcolare ogni iterazione in 10 secondi, ci vorranno circa due ore per ogni casella all'interno o vicina al lago di Mandelbrot. Anche se è una parte relativamente piccola della matrice 81 per 81, probabilmente ci vorrebbe un anno per completarla, anche lavorandoci diverse ore al giorno. Ecco dove diventano utili i computer al silicio.
Pubblicità
Consigli
- Perché z2 = (x2-y2, 2xy)?
- Per moltiplicare due numeri complessi come (a,b) con (c,d), usa la seguente formula, spiegata in questo articolo di Mathworld: (a,b)(c,d) = (ac - bd, bc + ad)
- Ricorda che un numero complesso è formato da una parte "reale" e da una "immaginaria"; quest'ultima è un numero reale moltiplicato per la radice quadrata di 1 negativo, spesso chiamato i. Il numero complesso (0,0), ad esempio, è 0+0i, e (-1,-1) è (-1) + (-1 * i).
- Ci stai ancora seguendo? Ricorda che i termini a e c sono reali, mentre b e d sono immaginari. Quindi, quando i termini immaginari vengono moltiplicati tra loro, la radice quadrata di 1 negativo moltiplicata per se stessa dà 1 negativo, annullando il risultato e rendendolo reale; al contrario, i numeri ad e bc rimangono immaginari, perché la radice quadrata di 1 negativo è ancora un termine di tali prodotti. Di conseguenza, ac - bd costituiscono la parte reale, mentre bc + ad quella immaginaria.
- Dal momento che stiamo elevando i numeri al quadrato invece che moltiplicarne tra loro due differenti, possiamo semplificare un po'; visto che a = c e b = d, abbiamo come prodotto (a2-b2, 2ab). E, dato che stiamo associando il "piano complesso" al "piano cartesiano", con l'asse x che rappresenta il "reale" e l'asse y che rappresenta l'"immaginario", lo descriveremo anche come (x2-y2, 2xy).
- Se stai calcolando ripetutamente una casella e ti accorgi che un risultato corrisponde esattamente a uno che hai già ottenuto per la stessa casella, sai di essere entrato in un circolo infinito; quella casella non fuggirà mai! Puoi quindi prendere una scorciatoia, colorare la casella con il tuo colore finale e passare alla successiva; (0,0) è, ovviamente, una di queste caselle.
- Vuoi sapere di più riguardo alla determinazione del valore assoluto di un numero complesso senza faticare con i calcoli?
- Il valore assoluto di un numero complesso (a,b) è la radice quadrata di a2 + b2, la stessa della formula del triangolo rettangolo, perché a e b vengono rappresentati sul reticolo cartesiano (le coordinate x e y, rispettivamente) ad angolo retto tra loro. Di conseguenza, visto che sappiamo che l'insieme di Mandelbrot è limitato al valore di 2, e che il quadrato di 2 è 4, possiamo evitare di pensare alle radici quadrate semplicemente vedendo se x2+y2 >= 4.
- Se uno dei cateti di un triangolo rettangolo è di lunghezza >=2, allora anche l'ipotenusa (lato diagonale) deve essere più lungo di 2. Se non capisci il perché, disegna alcuni triangoli rettangoli su un reticolo cartesiano e la cosa diventerà ovvia; oppure vedila in questo modo: 22=4 e, se a questo sommiamo un altro numero positivo (elevare al quadrato un numero negativo dà sempre come risultato un numero positivo), non possiamo ottenere qualcosa che sia meno di 4. Quindi, se il componente x o y di un numero complesso è di grandezza uguale o superiore a 2, il valore assoluto di tale numero è uguale o superiore a 2, ed è fuggito dall'insieme di Mandelbrot.
- Per calcolare la "larghezza virtuale" di ogni casella, dividi il "diametro virtuale" per il "numero di caselle meno uno". Negli esempi in alto usiamo un diametro virtuale di 4, perché vogliamo mostrare tutto all'interno del raggio di 2 (l'insieme di Mandelbrot è limitato dal valore di 2). Per l'approssimazione di lato 3, coincide con 4 / (3 - 1), che è 4 / 2, che a sua volta corrisponde a 2. Per il quadrato di lato 9, è 4 / (9 - 1), che è 4 / 8, che a sua volta corrisponde a ‘’’0,5’’’. Usa la stessa dimensione virtuale della casella sia per l'altezza che per la larghezza, anche se fai un lato più lungo dell'altro; in caso contrario, l'insieme risulterà deformato.
Avvertenze
- La matematica può dare assuefazione, come qualunque altra cosa, ma probabilmente non ti danneggerà il fegato né ti causerà il cancro ai polmoni.
Riferimenti
- La fonte javascript di queste tabelle; clicca le caselle per calcolare z e colorarle. Nota: funziona solo con un browser che supporta DOM, non Internet Explorer. Se funziona con il tuo browser, puoi visualizzare il valore aggiornato di z per ogni click cambiando display=c nell'URL con display=z, e puoi "barare" cliccando Auto-complete. Per altre opzioni vedi i commenti nella fonte.
- Questa ricerca è stata resa possibile, in parte, grazie a una sovvenzione da parte di City of the Sun, anche se le specifiche della ricerca non sono state coordinate né sostenute dal COSF.
- Insieme di Mandelbrot
- Rafael Bombelli, uno dei primi a spiegare i numeri immaginari.
- Benoit Mandelbrot
- Imaginary numbers
- Frattale



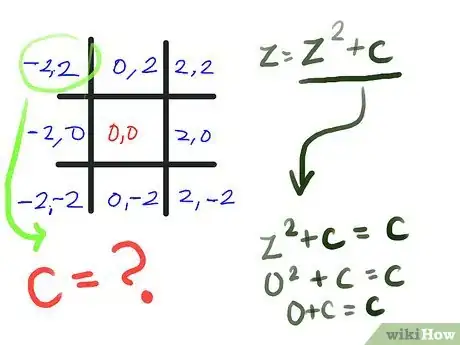






-to-Grams-(g)-Step-12-Version-4.webp)













-to-Grams-(g)-Step-12-Version-4.webp)
